
공분산을 활용한 콘크리트 오토인코더 기반 비지도 특징 선택 기법 연구
Copyright © 2024 Korean Institute of Broadcast and Media Engineers. All rights reserved.
“This is an Open-Access article distributed under the terms of the Creative Commons BY-NC-ND (http://creativecommons.org/licenses/by-nc-nd/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited and not altered.”
초록
특징 선택은 특징 공학의 한 과정으로 주어진 정형 데이터로부터 유의미한 특징 (feature, column)을 선택하는 것을 목적으로 한다. 딥러닝 기술이 다양한 분야에서 주목할 만한 수행 능력을 보여줌에 따라 특징 선택 분야에서도 딥러닝 기술 기반 연구가 활발히 이루어지고 있다. 본 논문에서는 concrete autoencoder 기반 선택 기법에 주목하였다. Concrete autoencoder란 autoencoder에 concrete random variable을 적용하여 유의미한 특징을 선택하는 기법이다. 하지만 concrete autoencoder 기법은 특징 선택 시 중복을 허용하고, 저차원 벡터 공간 내에서 데이터가 클래스별로 군집화 되지 않는다는 문제가 있다. 따라서 본 논문은 저차원 벡터 공간 내에서 데이터의 특징별 covariance를 고려하는 기법을 제시하고 다양한 데이터를 사용하여 이 기법을 평가한다. 제안하는 방법은 특히 유전적 정보를 담고 있는 바이오 데이터를 사용했을 때 우수한 성능을 보여준다.
Abstract
Feature selection is a feature engineering process that aims to select meaningful features from given structured data. As deep learning technology shows remarkable performance in various fields, deep learning-based research is also actively studied in the feature selection field. In particular, the concrete autoencoder method, which selects important features by applying a concrete random variable to the autoencoder, presented excellent performance in the field of feature selection. However, the concrete autoencoder allows overlap when selecting features and has the problem that data is not clustered by class within a low-dimensional vector space. In this paper, we propose a new feature selection technique that is based on the concrete autoencoder technique and can compensate for the shortcomings of the concrete autoencoder technique. The proposed method considers the covariance of data features in a low-dimensional domain to prevent the redundant feature selection while improving the clustering quality of samples within a low-dimensional space. The proposed technique showed superior feature selection performance compared to existing techniques, and its superiority is especially evident for biological data containing genetic information.
Keywords:
Feature selection, Unsupervised learning, AutoencoderⅠ. 서 론
인공지능 기술의 주목할 만한 발전에 따라서 대규모의 딥러닝 모델을 학습하기 위해 수집되는 데이터의 양도 급격히 증가하고 있다. 하지만, 이러한 대용량 학습 데이터에 대한 레이블링 (labeling)이나 데이터 클리닝 (data cleaning)[1]을 위한 인프라 구축은 금전적 기회비용뿐만 아니라 시간적 기회비용 또한 굉장히 크다. 따라서 대량의 원시 데이터를 딥러닝에 적합한 학습 데이터로 정제하는 특징 공학 (feature engineering)과 같은 기술들이 활발하게 연구되고 있다. 특징 공학은 일반적으로 원시 데이터 (raw data)들로 나열된 정형 데이터 (structured data)를 정제하는 기법을 연구하는 분야이다. 특징 공학에서는 데이터를 정제하는 방법에 따라 크게 데이터 클리닝, 특징 선택 (feature selection)[2], 특징 생성 (feature generation)[3]으로 분류한다. 그 중 특징 선택은 주어진 정형 데이터로부터 유의미한 특징 (feature, column)을 선택하는 것을 목적으로 한다.
전통적인 특징 선택 기법은 filter 기반 기법[4-6], wrapper 기반 기법[7,8]과 같은 rule-based 기법이 주로 연구되어 왔다. Filter 기반 기법은 각각의 특징마다 중요도 점수를 산출하여 계산된 점수가 높은 순으로 특징을 선택한다. 하지만 이러한 filter 기반 특징 선택 기법은 각각의 특징에 대한 중요도 점수를 개별적으로 산출하기 때문에 특징들 간의 상관관계를 고려하지 못한다는 단점이 있다. 이와는 다르게 wrapper 기반 특징 선택 기법은 데이터의 특징들로부터 부분 집합을 만들고 머신러닝 알고리즘을 이용해 원본 데이터를 대변할 수 있는 특징 부분 집합을 선택한다. 하지만 이러한 접근법은 특징 간의 상관관계를 고려할 수 있으나, 특징 선택 성능은 부분 집합을 구성하는 방식에 크게 의존하게 된다. 또한 데이터의 크기가 커질수록 연산 요구량이 과다해질 뿐만 아니라 연산 요구량 대비 선택된 특징의 분류 정확도가 크게 향상되지 않는다.
최근에는 딥러닝 기술이 영상 처리, 자연어 처리 등 다양한 분야에서 주목할 만한 수행 능력을 보여줌에 따라 특징 선택 분야에서도 딥러닝 기술을 활용한 특징 선택 기법이 활발하게 연구되고 있다. 딥러닝 기반의 특징 선택은 정답 데이터 사용 여부에 따라 지도 학습 (supervised)[9], 비지도 학습 (unsupervised)[10], 준지도 학습 (semi-supervised)[11] 으로 분류된다. 그중 각 샘플에 대한 클래스 혹은 회귀 값에 대한 정답을 사용하지 않는 비지도 학습 기반의 특징 선택이 활발히 연구되고 있다[12-16]. 대표적인 비지도 학습 기반 특징 선택 기법으로는 autoencoder feature selection (AEFS)[17] 기법이 있다. AEFS에서는 autoencoder의 인코더가 압축하는 과정에서 큰 가중치가 할당된 특징이 원본 데이터의 구조적 정보를 담고 있는 중요한 특징이라 가정한다. 따라서 데이터를 잘 복원할 수 있도록 reconstruct 손실과 특징 선택을 위한 L21-norm을 사용하여 모델을 학습한다. 하지만 AEFS는 구조가 간단하여 데이터의 구조를 잘 이해하지 못하고, L21-norm을 사용하기 때문에 미분 불가능한 파라미터가 생긴다. 또 다른 비지도 학습 기반 특징 선택 기법으로는 기존 AEFS의 인코더 부분에 concrete random variable[18]을 적용한 concrete selector layer를 만들어 특징 선택을 하는 concrete autoencoder feature selection (CAEFS)[19] 기법이 있다. 하지만 CAEFS는 특징 선택 시 중복을 허용하기 때문에 지정한 k개의 특징 선택 개수보다 적은 개수를 선택할 수 있다는 단점이 있다.
따라서 본 논문에서는 CAEFS 기법의 concrete selector layer 내의 hidden units의 특징별 covariance를 고려하여 특징 선택 시 중복 선택을 피할 수 있도록 유도하고, 기존 AEFS, CAEFS와 다르게 저차원 벡터 공간 내에서 데이터가 클래스별로 군집화 하는 효과 또한 얻을 수 있는 기법을 제안한다. 후술할 2장에서는 AEFS와 CAEFS를 포함한 기존 비지도 특징 선택 기법을 설명하고, 3장에서는 제안하는 방법인 concrete covariance autoencoder (CoCoder)에 대해 설명한다. 4장에서는 특징 선택에 주로 쓰이는 데이터를 사용하여 기존 비지도 학습 기반 특징 선택 기법과 제안하는 방법의 실험 결과를 비교하고, 5장에서는 결론을 마지막으로 본 논문을 마친다.
Ⅱ. 배경 지식 및 관련 연구
1. 기존 특징 선택 기법
특징 선택은 그림 1과 같이 방법론에 따라서 filter 기반 특징 선택 기법[4-6], wrapper 기반 특징 선택 기법[7,8], embedding 기반 특징 선택 기법[12,20,21]과 정답 데이터 사용 유무에 따라 지도 학습 (supervised)[9], 준지도 학습 (semi- upervised)[10], 비지도 학습 (unsupervised)[11]으로 나눌 수 있다.
Embedding 기반 기법은 인공 신경망 모델의 학습 과정에 특징 선택 과정을 포함시켜 모델이 직접 중요한 특징을 선택하는 방법이다. Embedding 기반 특징 선택 기법으로는 lasso method[21], global and local structure preservation (GLSP)[12]가 있다. Lasso method는 L1-norm을 정규화 (regularization) term으로 사용하여 모델을 학습한다. 손실 함수는 다음과 같다:
| (1) |
여기서 X는 입력 데이터, W는 가중치 행렬, Y는 정답 행렬이다. ∥.∥1은 L1-norm을 의미하고 λ는 L1-norm의 하이퍼파라미터를 나타낸다. Lasso method는 학습 시, L1-norm으로 인해 모델의 가중치 값이 0으로 수렴할 경우 가중치와 연결된 특징은 중요하지 않다고 판단한다. Embedding 기반 기법은 filter 기반 기법에 비해 특징 선택의 성능이 우수하고, wrapper 기반 기법에 비해서도 시간비용이 적게 든다. 이러한 장점으로 최근에는 embedding 기반 특징 선택 기법이 주목받고 있다. 후술할 AEFS[17]와 CAEFS[19] 그리고 본 논문에서 제안하는 방법 또한 embedding 기반 특징 선택 기법에 포함된다.
2. Autoencoder 기반 특징 선택 기법
Autoencoder 기법의 모델[22]은 일반적으로 인코더와 디코더, 두 모듈로 구성되어 있다. 인코더는 입력 데이터의 구조적인 정보를 담을 수 있는 저차원 벡터를 추정하고, 디코더는 이러한 저차원 벡터로부터 입력 데이터를 복원하도록 학습한다. 입력 데이터의 복원을 위한 autoencoder의 손실 함수는 다음과 같이 정의된다:
| (2) |
여기서 f()는 인코더, g()는 디코더, 는 입력 데이터를 나타낸다. N은 입력 데이터의 개수, 은 인코더의 가중치를 나타내며, 는 디코더의 가중치를 나타내고 두 모델의 가중치 집합은 로 표시한다. 는 Frobenius norm을 의미한다. 입력 데이터의 복원을 위해 압축 데이터의 노드 개수를 k로 설정하고 수식 2의 손실 함수를 최소화하는 방법으로 autoencoder 모델을 학습한다. 그림 2는 autoencoder의 전반적인 구조도를 보여준다. 그림 2에서 볼 수 있듯이 d차원의 입력 데이터 X로부터 인코더를 통해 저차원 벡터 를 추정하고, 이후 디코더에서는 저차원 벡터 h로부터 입력 데이터 X의 복원을 수행한다. 이러한 autoencoder 기반 특징 선택에서는 인코더가 입력 데이터를 압축하는 과정에서 큰 가중치가 할당된 특징이 원본 데이터의 구조적인 정보를 담고 있는 중요한 특징인 것으로 가정한다.
이러한 autoencoder를 기반으로 한 특징 선택 기법 중 가장 초기에 연구된 AEFS에서는 입력 데이터의 복원 학습뿐만 아니라 가중치의 희소성을 유도하여 특징 선택을 할 수 있도록 원본 데이터의 구조적 정보를 담은 인코더의 가중치 W(1)에 L21-norm을 적용한다. AEFS의 손실 함수는 다음 식 (3)과 같다:
| (3) |
여기서 ∥.∥2,1은 L21-norm, α는 L21-norm의 하이퍼파라미터, β는 정규화 (regularization)를 통해 가중치들의 스케일을 조정하기 위한 하이퍼파라미터다. 특징 선택을 위해 W(1)에 적용되는 L21-norm은 다음과 같이 계산된다:
| (4) |
여기서 W(1)은 인코더의 가중치, d는 입력 데이터의 특징 수, h는 압축 데이터 노드의 개수이다. j∈{1, ..., k}는 W(1)의 열 방향 인덱스, i∈{1, ..., d}는 W(1)의 행 방향 인덱스이다.
이렇듯 AEFS에서는 원본 데이터의 복원 학습과 함께 인코더의 가중치에 희소성을 유도하는 특징 선택 기법을 제안한다. 하지만 AEFS는 구조가 간단하여 전체 데이터 구조를 이해하지 못하거나, L21-norm에서 강제로 W(1)값의 일부를 0으로 바꾸는 구조이기 때문에, 모델의 성숙도를 고려한 특징 선택이 불가능하고, 미분 불가능한 파라미터들이 생성되기 때문에 해석이 어려운 데이터에서는 우수한 성능을 내기 어렵다.
3. Concrete autoencoder 기반 특징 선택
CAEFS는 AEFS의 L21-norm을 통한 가중치의 희소성을 유도하는 방법 대신 기존 AEFS의 인코더에 concrete random variable[18]을 적용한 concrete selector layer를 사용하여 특징을 선택하는 기법을 제안한다. 구체적으로는 concrete selector layer 내 hidden units을 임의의 특징 선택 개수 k로 추정하는 concrete selector layer와 두 개의 선형 레이어로 이루어진 디코더로 구성되어 있다. 그림 3은 concrete autoencoder의 구조를 보여준다.
CAEFS는 인코더의 가중치, 즉 W(1)에 concrete random variable을 적용하여 특징 선택을 학습한다. Concrete random variable이란 W(1)에 Gumbel distribution[23]으로 정의되는 노이즈를 추가하고 스케일링을 위한 매개변수인 T를 학습 epoch에 따라 annealing 하면서 나누어 준 variable을 말한다. 이를 통해 학습되는 인코더의 가중치를 continuous relaxation of the one-hot vector 형태로 유도할 수 있다. 이러한 concrete random variable은 다음과 같이 계산된다:
| (5) |
여기서 는 i∈{1, ..., k}번째 hidden unit과 입력 데이터의 j∈{1, ..., d}번째 특징이 연결된 가중치이고, 이다. 는 Gumbel distribution으로부터 독립적으로 추출된 값으로 에 더해진다. T는 사용자가 설정한 스케일링 값이고 학습이 진행됨에 따라 점점 0에 가까워지도록 설정한다. 는 에 concrete random variable을 적용하고 각 α(i)마다 소프트맥스를 취한 m(i)의 j번째 값이다. 학습 시 batch step에 따른 T의 annealing은 다음과 같이 적용된다:
| (6) |
여기서 E는 총 epoch 횟수, S는 한 epoch 안의 batch step 횟수를 의미한다. Tt는 현재 batch step에서의 T를 의미하고 t∈{1, ..., ES}이다. T0는 시작 온도, Tmin은 최소 온도, λ는 다음 batch step으로 넘어갈 때 이전 T에 곱해주는 값이다.
T가 높은 학습 초기에는 입력 데이터에 대한 W(1)의 가중치들이 균등 분포 (uniform distribution)를 형성하도록 유도할 수 있다. 이후 학습이 진행됨에 따라 T가 0에 가까워지면 concrete selector layer 내 hidden units과 연결된 각각의 가중치 벡터 m(i), {i = 1, ..., k}는 엔트로피가 최소화되는 방향으로 학습된다. 결과적으로 학습이 끝난 모델의 hidden units에는 입력 데이터의 특징 중 concrete selector layer로부터 선택된 특징들만 남게 된다.
Gumbel distribution은 학습이 진행되는 동안 concrete selector layer의 α(i)마다 Gumbel distribution으로부터 추출된 노이즈 값들을 더해줌으로써 특징 선택의 신뢰가 더 robust 할 수 있도록 만들어준다. 다시 말해 무작위성의 노이즈 요소가 추가되더라도 concrete selector layer에 의해 중요도를 가지는 특징들을 한 번 더 선별할 수 있도록 만드는 역할을 한다. 그림 4는 Gumbel distribution과 T에 따른 임의의 가중치 벡터의 변화를 보여주는 예시이다. 그림 4의 그래프 d축은 가중치의 인덱스, y축은 가중치의 크기를 나타낸다.
그림 4에서 볼 수 있듯이, T가 높을 때 임의의 벡터들은 균등 분포를 보이지만, T가 0에 가까워질수록 큰 가중치에만 집중하기 때문에 임의의 벡터는 희소적 형태를 띠게 된다. 종합하자면 concrete autoencoder를 학습하기 위한 손실 함수는 다음과 같다:
| (7) |
여기서 f ()는 concrete selector layer, g ()는 디코더, 는 입력 데이터, N은 입력 데이터 개수를 나타낸다. 는 concrete selector layer의 가중치, 는 디코더의 가중치, 두 모델의 가중치 집합은 로 표시되어 있다. Concrete autoencoder 기반 특징 선택 기법은 위 식 (7)과 concrete random variable을 사용하기 때문에 모델의 모든 파라미터는 미분가능하여 역전파 (backpropagation)를 적용할 수 있다. 학습을 마친 모델은 테스트 시 그림 5와 같이 concrete selector layer가 m(i)의 가중치들 중 가장 큰 가중치와 연결된 특징만 가져올 수 있도록 각 m(i)의 값들은 one-hot 벡터 형식으로 치환된다. 따라서 테스트 시 i번째 hidden unit, h(i)에는 X•m(i)로 계산된 가 저장된다.
하지만 CAEFS는 특징 선택을 위해 채택한 방식으로부터 기인하는 문제로 그림 5와 같이 특징 선택 시 중복을 허용한다는 점이 있다. 이는 특징 선택 시 concrete selector layer에서는 각각의 m(i)에서 가장 큰 가중치와 연결된 특징을 선택하기 때문이다. 이는 k개의 특징 선택 개수를 지정하였음에도 불구하고 중복된 특징을 제거하면 선택된 특징이 k개보다 적다는 문제가 생긴다. 이를 해결하기 위해 우리는 특징 선택이 중복되지 않도록 유도하는 방법으로 covariance concrete autoencoder를 제안한다. 자세한 사항은 다음 장에서 서술된다.
Ⅲ. 제안하는 방법
1. Covariance concrete autoencoder
기존 CAEFS[19]는 특징 선택 시 중복을 허용하기 때문에 지정한 k개 보다 특징이 적게 선택될 수 있다는 단점이 있다. 이러한 단점을 보완하기 위해 우리는 그림 3의 CAEFS의 구조는 따르지만, concrete selector layer 내 hidden units의 특징별 covariance를 낮추어 특징 선택이 최대한 중복되지 않도록 유도하는 covariance concrete autoencoder (CoCoder)기법을 제시한다. 또한 기존의 AEFS[17], CAEFS에서는 원본 데이터의 복원만 고려하기 때문에 concrete selector layer 내 hidden units은 저차원 벡터 공간 내에서 클래스별로 데이터가 군집화 되지 않는다. 하지만 제안하는 방법을 사용하면 hidden units의 특징별 covariance를 고려함으로써 중요한 특정 특징들이 hidden units에 집중되어 특징을 중복으로 선택할 수 있는 경우를 방지할 수 있을 뿐만 아니라, 서로 상관관계가 낮은 특징들을 선택할 수 있도록 유도하여 데이터를 저차원 벡터 공간 내에서 클래스별로 구분이 더 잘 되게끔 도와주는 군집 효과 또한 얻을 수 있다. 그림 6은 그림 3의 concrete selector layer 내 hidden units의 특징별 covariance를 계산하는 방법을 나타낸다.
그림 6과 같은 방법으로 입력 데이터로부터 off diagonal covariance matrix를 만들고 행렬의 제곱합의 평균을 계산하여 학습에 반영한다. 위 방법을 적용한 CoCoder는 다음 식 (8)과 같이 학습한다:
| (8) |
여기서 k는 hidden units의 개수, Cov는 off diagonal covariance matrix, λ는 covariance term의 하이퍼파라미터를 의미한다.
Ⅳ. 실험결과
이번 장에서는 전통적인 데이터에 대한 특징 선택 기법의 분류 성능을 비교한다. 특징 선택 기법을 사용하여 선택된 특징들로 머신러닝 random forest 분류 모델을 학습하고 테스트 정확도를 계산하여 비교하였다. Scikit-learn에서 제공하는 random forest 분류 모델을 사용하였고 하이퍼파라미터는 default 값으로 설정했다. 제안하는 방법 CoCoder의 알고리즘 성능을 비교하기 위해 AEFS[17], CAEFS[19] 방법들을 비교 기법으로 선정하였다.
실험 데이터로는 이미지 데이터인 MNIST[24]와 Fashion-MNIST[25]를 사용했고 바이오 데이터인 CLL-SUB-111[26], GLA-BRA-180[27], GLI-85[28], Prostate-GE[29]와 COLON[30]을 사용했다. 바이오 데이터란 마이크로어레이를 이용하여 백혈병과 신경교종 등 특정 질병과 관련된 유전자의 발현 정도를 측정한 데이터이다. 표 1은 특징 선택의 분류 성능 비교를 위해 사용된 데이터들의 사양을 나타낸 표이다.
특징 선택의 알고리즘 성능 비교를 위해서 모든 기법에서는 Adam optimizer를 사용했고 learning rate는 10-3으로 설정했다. Concrete autoencoder 기반 특징 선택과 CoCoder의 경우 시작 T는 10, 최소 T는 10-2로 설정하였고, 디코더의 hidden units는 128개로 설정했다. 학습과 검증 데이터의 수는 전체 데이터로부터 각각 8:2 비율로 나누어 진행했다. 각 모델들의 L21-norm, covariance term의 coefficient는 10~10-2까지 바꿔가며 분류 성능이 가장 높게 나온 결과를 채택했다. 이미지 데이터의 경우 reconstruction error에 비해 hidden units의 특징별 covariance 값이 낮아 covariance term의 coefficient를 높게 설정했을 때 특징 선택의 성능이 우수했다. 반면, 바이오 데이터에서는 이미지 데이터와 반대로 hidden units의 특징별 covariance 값이 reconstruction error에 비해 높았다. 따라서 이 경우에는 covariance term의 coefficient를 낮게 설정하여 특징 선택의 성능을 높일 수 있었다. 표 2는 제안하는 방법과 비교 방법들의 실험 결과를 보여준다.
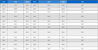
Classification accuracy of feature selection methods on benchmark datasetMeasure : mean of accuracy (mean of standard deviation)
유전자 정보를 담고 있는 바이오 데이터의 경우 고차원의 데이터이고 특정 특징은 자신의 정보뿐만 아니라 다른 특징의 유전적 정보 또한 대변할 수 있는 정보를 담고 있다. 따라서 이러한 바이오 데이터의 특성상 각 특징이 담고 있는 정보가 서로 중복되는 경향이 있어 이미지 데이터에 비해 해당 데이터는 특징별 covariance는 매우 높게 계산된다. 그 결과로 바이오 데이터에서 CAEFS 기법을 사용하면 데이터의 중요한 특징을 선택하기는 하지만 선택된 특징들의 정보가 중복되어 분류 성능이 낮게 나온다. 하지만 AEFS는 특징 선택 시 정보량 또한 고려하여 특징을 선택하기 때문에 정보를 중복하여 선택할 수 있는 CAEFS보다 분류 성능이 높게 나온다. 반대로 이미지 데이터의 경우는 중복되는 정보를 가진 특징이 바이오 데이터에 비해 적기 때문에 CAEFS는 AEFS보다 높은 분류 성능을 보인다.
결과적으로 제안하는 방법으로 특징 선택을 수행할 경우 concrete selector 내 hidden units의 특징별 covariance를 고려하여 기존 CAEFS의 중복된 정보를 가진 특징을 선택하는 문제를 해결함으로써 CAEFS보다 더 높은 분류 성능을 달성한 것을 확인할 수 있다. 이는 제안하는 방법을 통해 중요한 특징들이 중복 선택되지 않도록 유도하면서 상대적으로 중요도는 낮지만 디테일한 정보를 담고 있는, 즉 기존 CAEFS에서는 선택할 수 없는 특징 또한 선택할 수 있도록 유도함으로써 기존 AEFS, CAEFS보다 높은 분류 성능을 낼 수 있음을 확인할 수 있다.
Ⅴ. 결 론
본 논문에서는 비지도 학습 기반 특징 선택을 위해 압축 데이터의 특징별 covariance를 고려하는 기법을 제안했다. 결과적으로 CoCoder는 다양한 데이터에 대해서 분류 정확도가 평균적으로 높게 나왔으며 특히 특징 간 covariance가 높은 바이오 데이터에 대해 우수한 분류 성능을 보여줬다. Covariance term을 고려함으로써 기존 CAEFS[19]보다 선택되는 특징의 중복을 효과적으로 줄이고, 저차원 벡터 공간 내에서 데이터를 클래스별로 군집화 할 수 있었다. 따라서 CAEFS 기반의 특징 선택에서는 단순히 원본 데이터 복원을 위한 특징을 선택하는 것뿐만 아니라 압축한 hidden units에서의 특징 간의 covariance 또한 고려하여 선택하는 것이 유의미하다는 사실을 실험적으로 관측할 수 있었다. 하지만 제안하는 기법은 데이터 세트에 대한 covariance term의 coefficient dependency가 일부 관측된다. 따라서 추후 연구에서는 데이터 세트에 따라 adaptive하게 특징 선택을 적용할 수 있는 CoCoder 기반의 최적화 기법이 요구된다.
Acknowledgments
이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원 (No. RS2023-00208763), Few-shot learning을 위한 연상형 메모리 증대 신경망 네트워크 회로 및 아키텍처 개발 지원 (2022M3F3A2A01073944), 과학기술정보통신부 및 정보통신기획평가원의 인공지능융합혁신인재양성사업 연구 결과로 수행되었음 (IITP-2024-RS-2023-00254592).
References
-
Xu Chu, Ihab F. Ilyas, Sanjay Krishnan, and Jiannan Wang, “Data Cleaning: Overview and Emerging Challenges,” In Proceedings of the 2016 International Conference on Management of Data (SIGMOD '16), pp.2201–2206. June 2016.
[https://doi.org/10.1145/2882903.2912574]

-
Amir Moslemi, “A tutorial-based survey on feature selection: Recent advancements on feature selection,” Engineering Applications of Artificial Intelligence, Vol.126, Part D, pp.107136, November 2023.
[https://doi.org/10.1016/j.engappai.2023.107136]

-
G. Katz, E. C. R. Shin and D. Song, "ExploreKit: Automatic Feature Generation and Selection," 2016 IEEE 16th International Conference on Data Mining (ICDM), December 2016, pp.979-984.
[https://doi.org/10.1109/ICDM.2016.0123]

- Xiaofei He, “Laplacian Score for Feature Selection,” Advances in Neural Information Processing Systems, Vol.18, 2005. https://proceedings.neurips.cc/paper_files/paper/2005/file/b5b03f06271f8917685d14cea7c6c50a-Paper.pdf
-
Battiti R, “Using Mutual Information for Selecting Features in Supervised Neural Net Learning,” IEEE Transactions on Neural Networks, Vol.5, 4, pp.537-550, 1994.
[https://doi.org/10.1109/72.298224]

-
Cai Deng, He Xiaofei, Han Jiawei, Huang Thomas S. “Graph regularized nonnegative matrix factorization for data representation” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol.33, 8, pp.1548-1560, 2011.
[https://doi.org/10.1109/TPAMI.2010.231]

-
Narendra, Patrenahalli M., “A Branch and Bound Algorithm for Feature Subset Selection,” IEEE Transactions on Computers, Vol.C-26, Issue 9, pp.917-922, September 1977.
[https://doi.org/10.1109/TC.1977.1674939]

- Holland, John H. “Genetic Algorithms,” Scientific American, Vol.267, no. 1, pp.66-73, July 1992. http://www.jstor.org/stable/24939139
-
Samuel H. Huang, “Supervised feature selection: A tutorial,” Artificial Intelligence Research, Vol.4, 2, pp.22-37, 2015.
[https://doi.org/10.5430/air.v4n2p22]

-
Renato Cordeiro de Amorim, “Unsupervised feature selection for large data sets,” Pattern Recognition Letters, Vol.128, pp.183-189, December 2019.
[https://doi.org/10.1016/j.patrec.2019.08.017]

-
Razieh Sheikhpour, Mehdi Agha Sarram, Sajjad Gharaghani, Mohammad Ali Zare Chahooki, “A Survey on semi-supervised feature selection methods,” Pattern Recognition, Vol.64, pp.141-158, April 2017.
[https://doi.org/10.1016/j.patcog.2016.11.003]

-
X. Liu, L. Wang, J. Zhang, J. Yin and H. Liu, “Global and Local Structure Preservation for Feature Selection,” IEEE Transactions on Neural Networks and Learning Systems, Vol.25, no.6, pp.1083-1095, June 2014.
[https://doi.org/10.1109/TNNLS.2013.2287275]

- Xinxing Wu, Qiang Cheng, “Algorithmic stability and generalization of an unsupervised feature selection algorithm,” Advances in Neural Information Processing Systems, Vol.34, pp.19860-19875, 2021. https://proceedings.neurips.cc/paper_files/paper/2021/file/a546203962b88771bb06faf8d6ec065e-Paper.pdf
-
Deng Cai, Chiyuan Zhang, and Xiaofei He, “Unsupervised feature selection for multi-cluster data,” In Proceedings of the 16th ACM SIGKDD international conference on Knowledge discovery and data mining (KDD '10), pp.333-342, July 2010.
[https://doi.org/10.1145/1835804.1835848]

-
Mahsa Samareh Jahani, Gholamreza Aghamollaei, Mahdi Eftekhari, Farid Saberi-Movahed, “Unsupervised feature selection guided by orthogonal representation of feature space,” Neurocomputing, Vol.516, pp.61-76, January 2023.
[https://doi.org/10.1016/j.neucom.2022.10.030]

-
Pengfei Zhu, Wangmeng Zuo, Lei Zhang, Qinghua Hu, Simon C.K. Shiu, “Unsupervised feature selection by regularized self-representation,” Pattern Recognition, Vol.48, Issue 2, pp.438-446, February 2015.
[https://doi.org/10.1016/j.patcog.2014.08.006]

-
K. Han, Y. Wang, C. Zhang, C. Li and C. Xu, "Autoencoder Inspired Unsupervised Feature Selection," 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp.2941-2945, April 2018.
[https://doi.org/10.1109/ICASSP.2018.8462261]

-
Maddison, C. J., Mnih, A., and Teh, Y. W., “The concrete distribution: A continuous relaxation of discrete random variables,” arXiv, arXiv:1611.00712, , 2016.
[https://doi.org/10.48550/arXiv.1611.00712]

- Muhammed Faith Balin, Abubakar Abid, James Zou “Concrete Autoencoders: Differentiable Feature Selection and Reconstruction,” Proceedings of the 36th International Conference on Machine Learning, Vol.97, pp.444-453, June 2019. http://proceedings.mlr.press/v97/balin19a/balin19a.pdf
-
Wang, S., Tang, J. and Liu, H. “Embedded Unsupervised Feature Selection,” Proceedings of the AAAI Conference on Artificial Intelligence. Vol.29, 1, Feb 2015.
[https://doi.org/10.1609/aaai.v29i1.9211]

-
Robert Tibshirani, “Regression Shrinkage and Selection Via the Lasso,” Journal of the Royal Statistical Society: Series B (Methodological), Vol.58, Issue 1, January 1996, pp.267–288.
[https://doi.org/10.1111/j.2517-6161.1996.tb02080.x]

- Hinton, Geoffrey E and Zemel, Richard, “Autoencoders, Minimum Description Length and Helmholtz Free Energy,” Advances in Neural Information Processing Systems, Vol.6, 1993. https://proceedings.neurips.cc/paper_files/paper/1993/file/9e3cfc48eccf81a0d57663e129aef3cb-Paper.pdf
- Gumbel, Emil Julius, Statistical theory of extreme values and some practical applications a series of lectures, Vol.33. US Government Printing Office, 1954. https://books.google.co.kr/books?id=R8kCH9CIJrAC&hl=ko&pg=PR1#v=onepage&q&f=false
-
Y. Lecun, L. Bottou, Y. Bengio and P. Haffner, "Gradient-based learning applied to document recognition," Proceedings of the IEEE, Vol.86, no. 11, pp.2278-2324, November 1998.
[https://doi.org/10.1109/5.726791]

-
Han Xiao, Kashif Rasul and Roland Vollgraf, “Fashion-MNIST: a Novel Image Dataset for Benchmarking Machine Learning,” arXiv, 2017, 1708.07747, .
[https://doi.org/10.48550/arXiv.1708.07747]

-
Pengfei Zhu, Wangmeng Zuo, Lei Zhang, Qinghua Hu, Simon C.K. Shiu, “Unsupervised feature selection by regularized self-representation,” Pattern Recognition, Vol.28, Issue 2, pp.438-446, February 2015.
[https://doi.org/10.1016/j.patcog.2014.08.006]

-
Sun, Lixin, et al, "Neuronal and glioma-derived stem cell factor induces angiogenesis within the brain," Cancer cell, Vol.9, pp.287-300, April 2006.
[https://doi.org/10.1016/j.ccr.2006.03.003]

-
William A. Freije, F. Edmundo Castro-Vargas, Zixing Fang, Steve Horvath, Timothy Cloughesy, Linda M. Liau, Paul S. Mischel, Stanley F. Nelson, “Gene Expression Profiling of Gliomas Strongly Predicts Survival,” Cancer Res, Vol.64, 18, pp.6503-6510, September 2004.
[https://doi.org/10.1158/0008-5472.CAN-04-0452]

-
Petricoin EF 3rd, Ornstein DK, Paweletz CP, et al. “Serum proteomic patterns for detection of prostate cancer,” J Natl Cancer Inst, Vol.94, 20, pp.1576-1578, October 2002.
[https://doi.org/10.1093/jnci/94.20.1576]

-
U. Alon, N. Barkai, D. A. Notterman, K. Gish, S. Ybarra, D. Mack, and A. J. Levine, “Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays,” Proceedings of the National Academy of Sciences, Vol.96, no. 12, pp. 6745–6750, June 1999.
[https://doi.org/10.1073/pnas.96.12.6745]


- 2019년 3월 ~ 현재 : 동국대학교 AI소프트웨어융합학부 학사
- ORCID : https://orcid.org/0009-0006-7472-5612
- 주관심분야 : 컴퓨터 비젼, 머신러닝, 딥러닝

- 2019년 3월 ~ 현재 : 동국대학교 AI소프트웨어융합학부 학사
- ORCID : https://orcid.org/0009-0008-6989-968X
- 주관심분야 : Feature selection, 준지도 학습, 딥러닝

- 2010년 : 서강대학교 전자공학과 학사
- 2015년 : 포항공과대학교 전자전기공학부 박사
- 2017년 : LG 디스플레이 선임연구원
- 2019년 : 대구대학교 전자전기공학부 조교수
- 2019년 ~ 현재 : 동국대학교 AI소프트웨어융합학부 부교수
- ORCID : https://orcid.org/0000-0003-4251-7131
- 주관심분야 : 영상처리, 컴퓨터 비젼, 딥러닝






