동적 이미지 합성을 위한 4D Gaussian Splatting 기법 비교 및 연구 동향
Copyright © 2025 Korean Institute of Broadcast and Media Engineers. All rights reserved.
“This is an Open-Access article distributed under the terms of the Creative Commons BY-NC-ND (http://creativecommons.org/licenses/by-nc-nd/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited and not altered.”
초록
Novel View Synthesis 분야에서 동적 장면을 표현하고 랜더링 하는 것은 중요하면서도 도전적인 연구 분야로 자리 잡고 있다. 최근 등장한 Gaussian Splatting 기술은 정적 장면에서 뛰어난 표현 성능과 실시간 랜더링을 보여주었다. 그러나 이 기술을 동적 장면에 적용하기 위해 독립적인 프레임에 대해 3D Gaussian을 학습함으로써 합성 품질이 저하되고 많은 저장 공간을 필요로 하는 등의 비효율성이 발생한다. 이러한 한계를 극복하기 위해 최근 4D Gaussian Splatting 알고리즘들이 활발히 연구되어 동적 장면으로의 확장을 가능하게 하고 있다. 본 논문에서는 Deformable 3D Gaussian, 4D-GS, SC-GS, 그리고 Spacetime Gaussian, 총 네 개의 4D Gaussian Splatting을 살펴보고 성능 비교 및 장단점을 분석하였다.
Abstract
The field of Novel View Synthesis has established itself as an important yet challenging area of research, particularly in representing and rendering dynamic scenes. Recently introduced Gaussian Splatting techniques have demonstrated great performance and real-time rendering capabilities for static scenes. However, when applying this technique to dynamic scenes by learning 3D Gaussians for independent frames, inefficiencies arise, such as degraded synthesis quality and the requirement for significant storage space. To overcome these limitations, 4D Gaussian Splatting algorithms have been developed, enabling the extension to dynamic scenes. In this paper, we examine four 4D Gaussian Splatting methods: 4D-GS, SC-GS, Spacetime Gaussian, and Deformable 3D Gaussian. We compared the performance of each 4D Gaussian Splatting model and analyzed their strengths and weaknesses
Keywords:
3D Gaussian Splatting, 4D Gaussian Splatting, Dynamic sceneⅠ. 서 론
3D Gaussian Splatting[1]은 신경망 중심의 정적 장면 합성 체계를 Gaussian 중심으로 변화시킴으로써 3D 장면 합성 분야에 큰 영향을 미치고 있다. 기존의 신경망은 장면의 모든 세부사항을 예측하려 했기 때문에 학습과 랜더링에 많은 비용과 시간이 소요된다. 그러나 3D Gaussian Splatting은 Gaussian 정보만 저장하면 되므로 많은 학습을 필요로 하지 않으며, 이전 연구들에 비해 월등히 향상된 학습 및 랜더링 속도를 보인다. 최근 3D Gaussian Splatting에 대한 연구는 활발히 이루어지고 있으며 이는 정적 장면을 합성하기에는 적합하지만, 동적 장면을 표현하지 못한다는 한계가 있다. 이를 4차원 표현으로 확장하기 위한 가장 간단한 방법은 각 timestamp마다 3D Gaussian을 구성하는 것이지만, 저장 용량이 크게 증가하며 시간적 일관성을 유지하기 어렵다는 단점이 있다.
최근에는 동적 장면을 표현하기 위하여 3D Gaussian을 먼저 추정하고 프레임 별 deformation을 예측하여 저장 공간의 효율성을 높이면서 시간적 일관성도 유지할 수 있는 방법론이 연구되고 있다. 대표적으로, Deformable 3D Gaussian[2]은 3D Gaussian의 중심 좌표와 시간을 입력으로 받아 위치, 회전, 크기에 대한 변형을 예측하는 deformation field를 통해 동적 영역을 표현한다. 4D-GS[3]는 3D Gaussian의 위치와 시간인 4차원 정보를 입력으로 받고, 이를 2차원 정보 여러 개로 나누어 표현하는 hexplane으로 변형하여 각 프레임 별 deformation을 추정한다. SC-GS[4]는 3D Gaussian 위치 중 대표 control point를 지정하고, 해당 포인트의 deformation을 추정한 후, 이웃한 control point 간의 보간을 통해 전체 Gaussian의 움직임을 도출하는 방법을 사용한다. 이를 통해 효율적이면서 시간적 일관성을 유지할 수 있다는 장점이 있다. 마지막으로 Spacetime Gaussian[5]은 temporal opacity와 parametric motion/rotation을 통해 주요 Gaussian 정보들을 다항식 형태로 모델링 함으로써 성능을 끌어올렸다.
본 논문에서는 최근 활발하게 연구되고 있는 “동적 이미지 합성을 위한 4D Gaussian Splatting 기법”의 현황과 동향을 살펴보고자 한다. Ⅱ장에서는 동적 이미지 합성을 위한 4D Gaussian Splatting 기법들의 핵심 방법론과 contribution에 대해 자세히 알아보고자 한다. Ⅲ장에서는 다양한 비디오에 대한 각 모델의 학습 결과를 정성적, 정량적으로 비교 분석하여 각 모델의 장단점을 알아볼 것이다. IV장에서는 분석한 결과를 바탕으로 각 동적 이미지 합성을 위한 4D Gaussian Splatting 기법의 특징을 설명하며 향후 연구 방향에 대해 논의해 볼 것이다.
Ⅱ. 동적 이미지 합성을 위한 4D Gaussian Splatting 기법 비교 및 연구 동향
1. 3D Gaussian Splatting[1]
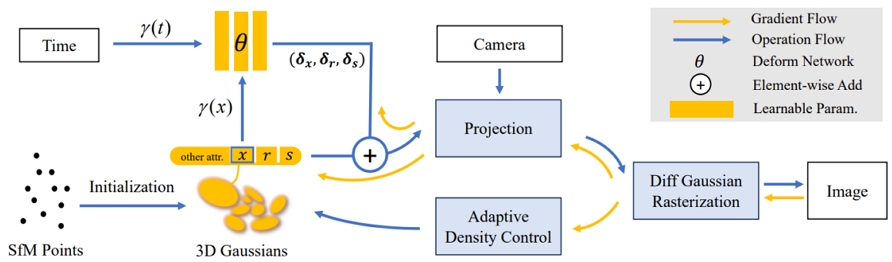
3D Gaussian Splatting[1]은 다양한 위치, 불투명도, 색깔, 회전, 크기 등의 파라미터를 가지는 타원체인 3D Gaussian을 활용하여 3D 구조를 표현하는 방법론이다. 3D Gaussian Splatting[1] 알고리즘의 전체 흐름도는 그림 1과 같다. 구체적으로, 먼저 COLMAP과 같은 Structure from Motion (SfM) 기법을 통해 initial point cloud를 추정하고, point cloud의 좌표에 3D Gaussian의 중심을 위치하도록 초기화시킨다. 그 다음, 3D Gaussian들을 입력으로 받은 camera pose를 이용하여 이미지 평면으로 2D projection 시킨다. 이후 빠른 rasterization을 위해 이미지를 타일화 시키고, 각각의 타일에 대해 다음과 같은 rasterization 과정을 진행한다. 먼저, 각 3D Gaussian의 깊이 정보를 바탕으로 키 값을 부여하여 이미지 평면에서 가까운 3D Gaussian부터 정렬을 시킨다. 다음으로, 정렬된 Gaussian들을 배경 이미지와 차례로 알파 블렌딩을 수행한다. 위 과정을 마치고 나면 3D Gaussian을 통해 랜더링 된 2D 이미지가 생성되며, 이를 ground truth 이미지와 비교하여 손실(Loss)과 그레디언트를 얻고, 역전파를 통해 3D Gaussian을 학습시킨다. 또한 적응적 밀도 조절을 통해 Gaussian의 학습이 어려운 영역에 Gaussian을 복제하거나 제거함으로써 장면을 잘 표현하지 못하는 부분을 보완한다. 이러한 학습 과정을 여러 다각도 이미지에 대해 반복하여 최적화하면, 최종적으로 3D 장면에 대해 중심 위치를 x로 가지는 아래와 같은 Gaussian으로 표현 가능하다.
| (1) |
여기서 중심위치 χ는 Gaussian의 mean을 의미하며 Σ는 Gaussian의 covariance marix를 의미한다.
3D Gaussian Splatting은 빠른 학습 속도를 보이고 실시간 랜더링을 가능하게 하여 괄목할 만한 성능을 이끌어냈지만, 그 결과가 정적인 장면에 국한되는 한계점을 가진다. 최근에는 이러한 한계점을 개선하기 위해 시간에 따른 변화 정도를 표현할 수 있는 deformation 기반의 방법들이 활발히 연구되고 있다. 본 논문에서는 3D Gaussian Splatting을 개선하고 발전시킨 모델 중, 정적 장면 합성에만 국한되지 않고 동적 장면에 대한 합성이 가능하도록 하는 모델들에 대해 분석하고, 그 동향에 대해서 살펴보고자 한다. 먼저 3D Gaussian의 중심 위치와 시간을 입력으로 받아 deformation을 예측하는 Deformable 3D Gaussian[2]에 대해 알아보고자 한다. 다음으로 4차원의 deformation 정보를 2차원 plane 기반 tensor decomposition으로 표현하는 4D-GS[3] 그리고 control point를 도입해 회전과 변형을 구하고, 이를 통해 Gaussian의 움직임을 효율적으로 표현한 SC-GS[4]에 대해 살펴보고자 한다. 마지막으로 Gaussian의 각 파라미터를 시간에 대한 파라미터로 표현하여 동적 장면을 표현한 Spacetime Gaussian[5]에 대해서 알아보고자 한다.
2. Deformable 3D Gaussians for High-Fidelity Monocular Dynamic Scene Reconstruction[2]
Deformable 3D Gaussian[2]은 3D Gaussian Splatting과 달리 Gaussian의 시간에 따른 변화를 예측하여 동적 장면을 합성하는 것이 목표로 하며, 전체적인 구조는 그림 2와 같다. 구체적으로, MLP를 통해 deformation을 학습하는 것으로 이루어지며, 시간 t와 3D Gaussians의 중심 위치 x를 입력으로 받아 Gaussian의 위치, 회전, 크기에 대한 변화량 δχ, δr, δs을 출력한다. 이후 출력된 변화량을 3D Gaussians에 더해 시간에 따른 장면을 합성할 수 있다. 위치, 회전, 크기에 대한 변형을 계산하는 Deform Network에 대한 수식은 다음과 같다:
| (2) |
여기서 sg(ㆍ)는 stop-gradient operation, γ(ㆍ)는 positional encoding, Fθ(ㆍ)는 deformation field를 의미하며. δχ, δr, δs는 각각 위치, 회전, 크기에 대한 변화량을 의미한다.
3. 4D-GS: 4D Gaussian Splatting for Real-time Dynamic Scene Rendering[3]
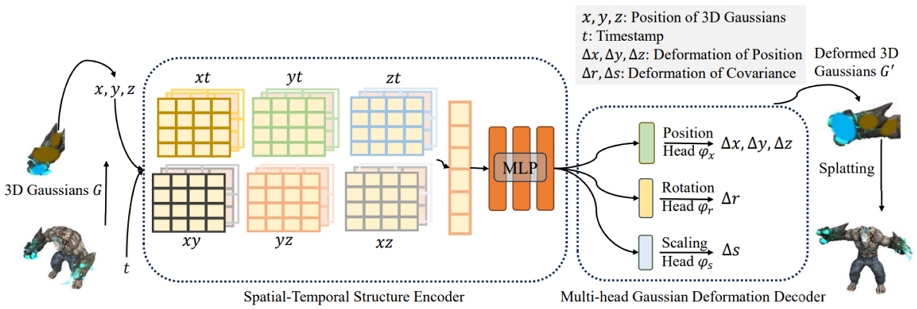
4D-GS[3]는 그림 3과 같이 Deformable 3D Gaussian[2]의 동일한 구조에 학습 시간을 단축시키기 위해 4차원 정보를 2차원 정보로 변환시키는 hexplane을 encoder에 추가하고 lightweight MLP로 변경했다. 구체적으로, input으로 3D Gaussains의 위치와 시간 t를 받아 Spatial-Temporal Structure Encoder의 hexplane을 통해 4D informtaion을 2D informtaion으로 처리하고 이를 MLP를 통과시켜 feature로 인코딩한다. 이후 Multi-head Gaussian Deformation Decoder의 MLP에 feature를 input으로 넣고 처리하여 position, rotation, scaling의 deformation을 예측한다. 학습 과정은 coarse-to-fine으로 분리되어 coarse 단계에서는 3D Gaussians만 학습하고 fine 단계에서 Deformation Network를 함께 학습한다. Deformation Network에서 예측된 deformation을 Gaussians에 더해 동적 장면을 표현하고 그에 대한 구체적인 수식은 다음과 같다:
| (3) |
여기서 χ, r, s는 각각 Gaussian의 position, rotation, scaling을 의미하며 Δχ, Δr, Δs는 각각 이들의 deformation을 의미한다.
4. SC-GS: Sparse-Controlled Gaussain Splatting for Editable Dynamic Scenes[4]
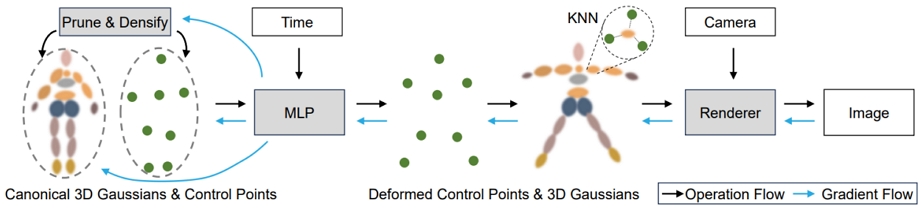
SC-GS[4]는 Gaussian보다 훨씬 적은 수의 대표 control point를 도입하여 이들의 deformation을 예측하고 이를 바탕으로 보간을 진행하여 전체 Gaussian의 deformation을 예측하는 특징을 가지고 있다. 구체적으로, 그림 4와 같이 먼저 전체 Gaussians의 수보다 훨씬 적은 수의 제어점을 도입하고 각 제어점의 위치 및 회전과 이동의 변화를 MLP를 통해 예측한다. 다음으로 Linear Blend Skinning을 사용해 앞서 구해진 control point들의 deformation을 보간하여 Gaussian motion field를 도출한다. 구체적으로 control point들을 통해 개별 Gaussian의 속성들의 deformation을 구하는 방법을 살펴보겠다.
시간 t에서의 Gaussian j의 회전을 나타내는 쿼터니언 는 다음과 같다:
| (4) |
여기서 는 시간 t에서의 j 번째 Gaussian의 회전을 나타내는 쿼터니언이다. 이를 구하기 위해서 Gaussian j의 원래 회전을 나타내는 qj와 의 쿼터니언 곱을 계산하는데 이때, Nj개 인접한 제어점들의 집합을 상대로 제어 포인트별 각 Gaussian의 보간 가중치wjk와 제어점 k에서의 회전 변화를 나타내는 쿼터니언 을 곱하여 제어점 k에서의 회전을 보간한다.
Gaussian j의 중심 위치를 나타내는 는 다음과 같다:
| (5) |
여기서 제어점의 영향을 나타내는 보간 가중치 wjk, 제어점 k의 회전 변환을 나타내는 행렬 , 제어점 k의 위치를 나타내는 pk, 제어점 k의 시간 t에서의 이동 변환을 나타내는를 이용하여 이를 표현한다.
또한 더 나은 동적 장면 합성을 위해 As Rigid As Possible(ARAP) Loss를 도입하여 인접한 제어점들의 모션이 일관되도록 유도한다. 마지막으로 적응형 밀도 조절 전략을 사용하여 복잡한 모션을 모델링하는 영역에 더 많은 제어점을 추가하고 단순한 모션을 모델링하는 영역에서는 불필요한 제어점을 제거한다. 이때 제어점의 영향력이 적거나 Gaussian의 모션에 충분히 기여하지 못하는 경우 해당 제어점을 삭제하고 Gaussian이 높은 gradient 값을 가지는 경우 복제하여 새로운 제어점을 추가한다. 이 과정을 통해 복잡한 모션을 더 잘 반영할 수 있도록 제어점의 분포를 최적화하고 인접한 제어점의 모션이 일관되도록 유도하여 모션의 품질을 향상시킨다.
5. Spacetime Gaussian: Feature Splatting for Real-Time Dynamic View Synthesis
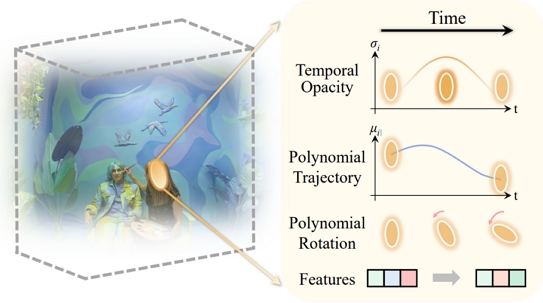
Spacetime Gaussian[5]은 4D 동적 장면을 표현하기 위해 3D Gaussian에 다항식과 Gaussian 분포를 이용해 모델링한 파라미터들을 제안한다. Spacetime Gaussian[5]의 네트워크 구조는 그림 5와 같다. 구체적으로 영상 내에서 나타나거나 사라지는 장면 콘텐츠를 효과적으로 모델링하기 위해 불투명도는 1D Gaussian으로 모델링하고, 위치와 회전은 다항식 형태로 모델링한다. 또한 기존에 사용되었던 구면 조화 함수 대신 특징 벡터를 사용하여 색상을 더 간결하고 효율적으로 표현하는 방법을 제안한다.
투명도를 시간에 따른 파라미터로 표현한 것은 다음과 같다:
| (6) |
여기서 시간과는 무관한 기본 투명도 , Gaussian이 가장 잘 보이는 시점을 나타내는 , Gaussian이 높은 투명도를 유지하는 시간의 범위를 나타내는 를 이용한 1D Gaussian으로 시간에 따른 투명도를 표현한다.
시간 t에서 공간적 위치를 의미하는 μi(t)를 표현하는 수식은 다음과 같다:
| (7) |
여기서 μi(t)는 학습 중에 최적화되는 다항식 계수 bi,k, Gaussian이 시간적으로 가장 잘 보이는 시점을 나타내는 를 이용하여 다항식 함수로 표현한다.
시간 t에서 회전을 의미하는 qi(t)를 표현하는 수식은 다음과 같다:
| (8) |
여기서 qi(t)는 학습 중에 최적화되는 다항식 계수 ci,k, Gaussian이 시간적으로 가장 잘보이는 시점을 나타내는 를 이용하여 다항식 함수로 표현한다.
각 알고리즘의 요소 별 특징을 정리하면 표 1과 같다.
Ⅲ. 네트워크 성능 비교
이번 장에서는 딥러닝 기반 4D Gaussian Splatting에서 합성된 장면들의 결과와 지표를 살펴보고, Deformable-3DGS[2], 4D-GS[3], SC-GS[4], Spacetime[5] 모델들의 성능을 평가하고자 한다. 성능 평가를 위해 각 논문의 저자들이 공개한 코드 및 모델로 실험을 진행하였다. 3DGS[1]는 각 frame 별 독립적으로 Gaussian Splatting을 학습한 결과이다. 비교 성능 지표로 원본 이미지와 합성 이미지 간의 차이를 측정하는 Peak Signal to Noise Ratio(PSNR), 두 이미지 간의 구조적 유사성을 측정하는 지표인 Structural Similarity Index Measure(SSIM)[6], 그리고 optical flow model[7]을 통해 전체 프레임에서 정적 영역에 해당하는 마스크를 추출 후 PSNR을 계산하는 Masked Peak Signal to Noise Ratio(M-PSNR)을 사용했다. 기존 논문들[2][3][4][5]의 실험 환경과 동일하게 real-world 시나리오에서 평가할 수 있는 Neural 3D Video dataset[8]을 사용하여 성능 평가를 하였다. 해당 데이터셋은 6개의 동적 장면을 포함하며 개별 장면을 15-20개의 고정된 카메라로 촬영하였으며 이를 300프레임 샘플링하여 사용하였다. 또한, Center view를 test 데이터로 활용하였으며 높이와 너비를 1/2로 줄여 1352x1014의 해상도로 랜더링 성능을 평가하였다.
1. 정량 평가
표 2, 표 3을 보면 PSNR과 SSIM[6] 지표에서 Spacetime[5]이 가장 높은 성능을 보여주어 동적 장면 복원에 대해 합성 품질과 구조적 유사성이 가장 뛰어남을 알 수 있다. 이는 시간적 불투명도와 모션을 파라미터화하여 다항식 형태로 나타내는 방법론이 시간에 따른 변위 정보를 MLP를 통해 학습하는 deformation 기반의 방법론보다 동적 장면에 대한 복원력이 뛰어남을 나타낸다. 또한 M-PSNR 지표에서도 높은 점수를 보여주어 동적 영역과 정적 영역 시간적 일관성이 뛰어남을 확인할 수 있다. 반면, PSNR 점수가 가장 낮은 SC-GS[4]가 M-PSNR에서 가장 높은 것을 확인할 수 있다. 이는 전체 Gaussian들의 변형을 개별적으로 예측하는 다른 deformation 기반의 모델들에 비해 특정 제어점을 통해 동적 영역을 표현하는 방법론이 정적인 영역을 훼손하지 않고 일관성을 높여주는 것을 나타낸다. 또한 3DGS[1]는 다른 알고리즘에 비해 모든 지표에서 성능이 떨어졌는데, 이는 frame 별로 Gaussian을 독립적으로 학습하는 방법론보다 canonical Gaussian에 시간에 따른 deformation 값을 예측하는 방법론이 일관성 및 동적 장면을 복원하는 성능이 뛰어남을 나타낸다.

Quantitative results of 3DGS[1], Deformable-3DGS[2], 4D-GS[3], SC-GS[4], and Spacetime[5] on Neural 3D Video dataset[8]

Quantitative results of 3DGS[1], Deformable-3DGS[2], 4D-GS[3], SC-GS[4], and Spacetime[5] on ETRI dataset
표 4는 위 실험 결과를 바탕으로 각 모델의 특징 및 장단점을 합성 품질(Quality), 시간적 일관성(Temporal consistency), 학습 시간(Training time), 프레임 레이트(FPS)로 비교 정리한 것이다. 먼저, Deformable-3DGS[2]는 추가적인 MLP를 통해 동적 영역에 대한 표현력을 강화하여 시간적 일관성을 유지하지만, 학습 시간이 오래 걸리는 단점이 있다. 반면, 4D-GS[3]는 Deformable-3DGS[2]보다 Light-weight MLP로 교체함으로써 학습 시간을 단축시켰으나, 성능 차이를 Hexplane이 완전히 보완하지 못해 시간적 일관성이 저하되었다. 이로 인해 그림 6에서 볼 수 있듯이, 랜더링된 이미지에 흐릿해지는 아티팩트가 발생한다. 한편, SC-GS[4]는 제어점의 deformation만을 학습함으로써 정적 영역에서의 잘못된 모션 추정을 방지하여 시간적 일관성이 높지만, 학습 시간이 오래 걸린다는 단점이 있다. 마지막으로, Spacetime[5]은 Deformation Network 기반 알고리즘들에 비해 빠른 학습 시간과 가장 높은 프레임 레이트를 보여준다. 또한, 시간에 따른 특성을 추가하여 변형을 학습하는 방법론이 동적 및 정적 영역 모두에서 뛰어난 시간적 일관성을 유지하며, 특징 벡터를 이용해 색상을 표현함으로써 높은 퀄리티의 이미지를 합성이 가능하다.
2. 정성 평가
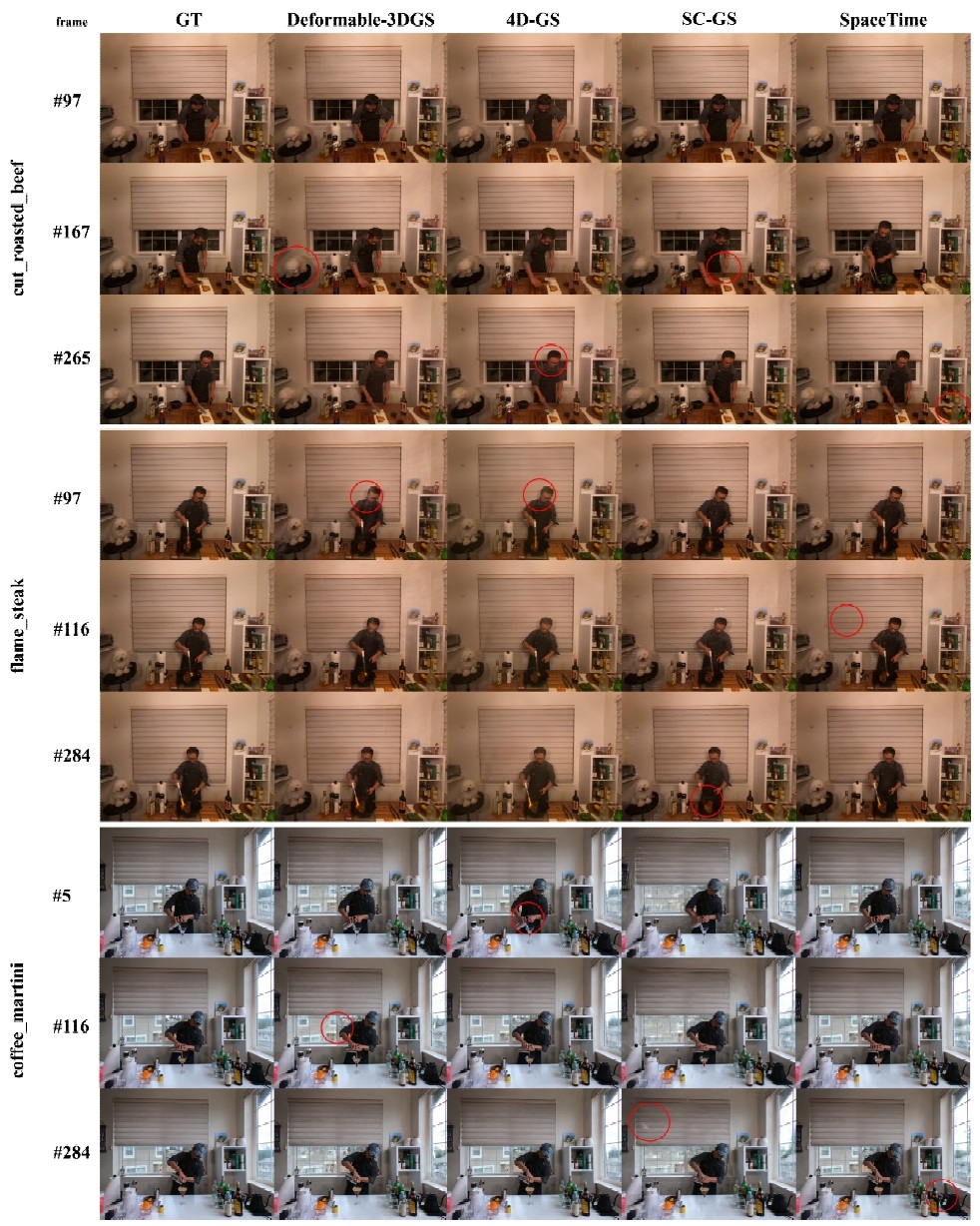
그림 6은 각 알고리즘의 성능을 비교한 결과를 보여준다. 먼저 Cut_roasted_beef와 Flame_steak 데이터에서, 4D-GS[3] 알고리즘은 객체들의 움직임을 세밀하게 추정하지 못하여 동적 영역의 복원력이 떨어졌고, 남자의 얼굴 영역에서 아티팩트가 발생하여 시공간적 일관성이 부족함을 확인할 수 있었다. Deformable-3DGS[2]는 4D-GS[3]보다 동적 영역의 모션을 더 잘 표현하였으나, 역시 동적 영역에 아티팩트가 발생하였고, 강아지의 몸통 부분이 사라져 시간적 일관성이 저하된 것을 확인할 수 있었다. SC-GS[4]의 경우, 집게와 불과 같은 복잡한 모션을 세밀하게 추정하지 못하여 동적 영역의 복원력이 낮았다. Spacetime[5]은 전반적으로 잘 복원되었지만, 정적 영역에서 모션이 잘못 학습되어 아티팩트가 발생했다. 마지막으로 Coffee_martini 데이터에서 Deformable-3DGS[2]와 SC-GS[4]는 모션을 정확히 추정하여 시간적 일관성은 높았으나, 배경 영역의 Gaussian 자체를 제대로 복원하지 못해 정적 영역에서의 복원에 실패했다. Spacetime[5]은 동적 및 정적 영역 모두에서 전반적으로 높은 성능을 보여주었으나, 정적 영역에서 아티팩트로 인해 깜빡거림(flicker) 현상이 발생한 것을 확인할 수 있었다.
그림 7은 각 알고리즘의 성능을 비교한 결과를 보여준다. 먼저 S01t01와 S01t08 데이터에서, 4D-GS[3] 알고리즘은 객체들의 움직임을 세밀하게 추정하지 못하여 동적 영역의 복원력이 떨어져 손이 사라지고 손에 든 물체가 없어지는 등의 결과를 보였고, 남자의 어깨 영역에서 아티팩트가 발생하여 시공간적 일관성이 부족함을 확인할 수 있었다. Deformable-3DGS[2]는 4D-GS[3]보다 동적 영역의 모션을 더 잘 표현하였으나, 역시 동적 영역에 아티팩트가 발생하였다. SC-GS[4]의 경우, 모션이 큰 S01t01 데이터의 몸쪽이 합성되지 않아 동적 영역의 복원력이 매우 낮았고 마찬가지로 S01t08 데이터에서도 모션이 큰 부분이 blur하게 표현되는 등 동적 영역 표현에 문제를 가졌다. Spacetime[5]은 전반적으로 잘 복원되었지만, 정적 영역에서 모션이 잘못 학습되어 아티팩트가 발생했다.

Qualitative results of 3DGS, 4D-GS[3], Deformable-3DGS[2], SC-GS[4], and Spacetime[5] on ETRI dataset
결론적으로, Spacetime[5]이 동적 및 정적 영역에서 가장 우수한 성능을 보였다. 이 알고리즘은 다른 Deformation 기반 알고리즘에 비해 복잡한 모션을 더 잘 학습하고, 정적 영역의 복원력이 뛰어났다. SC-GS[4]는 정적 영역의 일관성에서는 가장 높은 성능을 보였으나, 정적 영역 자체의 복원력은 떨어졌고, 모션이 복잡한 데이터에 취약한 것으로 나타났다. 이는 전체 Gaussian의 모션을 학습하지 않고, 제어점들의 변위 정보를 보간하는 방식으로 표현하기 때문에 모션이 흔들리거나 번지는 현상이 발생했다. Deformable-3DGS[2]와 4D-GS[3]는 모션 영역이 커질수록 표현력이 떨어져 시간적 일관성을 유지하지 못하였으며 정적 영역의 복원력도 저하되는 결과를 보였다.
Ⅳ. 결 론
본 논문에서는 동적 이미지 합성을 위한 4D Gaussian Splatting 기법의 현황 및 동향에 대해 살펴보았다. Deformation field를 도입해 동적 영역(모션)을 표현하기 위해 Gaussian들의 변형을 예측한 Deformable 3D Gaussian[2], 이 모델의 구조를 개선하고 4차원의 정보를 2차원화 하는 hexplane을 encoder에 추가한 4D-GS[3], 제어점을 활용해 효과적으로 Gaussian의 동적 영역(모션)을 표현한 SC-GS[4], Gaussain의 각 파라미터들을 시간에 대한 파라미터로 변환하여 성능을 끌어올린 Spacetime Gaussian[5] 등, 동적 이미지 합성을 위한 4D Gaussian Splatting 연구들은 꾸준히 모델을 개선하고, 학습 방법을 최적화하는 방식으로 연구가 진행되고 있다.
각 모델들은 동적 장면을 합성하기 위해 deformation을 추정한다는 공통점이 있지만, 네트워크 구조에 따라 장단점이 다르다. Deformable 3D Gaussian[2]는 deformation field를 활용해 변형을 예측하고 동적 장면을 합성할 수 있지만 일관된 정적 영역의 표현이 부족하다. 4D-GS[3]는 hexplane을 이용해 더 개선된 성능을 보였지만 마찬가지로 정적 영역을 잘 표현하지 못하는 문제를 가지고 있다. 제어점을 활용해 모션을 표현하는 SC-GS[4]는 정적 영역 표현에 대해 훌륭한 성능을 보이지만 상대적으로 동적 영역 표현이 만족스럽지 못하고, Spacetime Gaussian[5] 또한 Gaussian의 각 파라미터를 시간에 대한 파라미터로 만들어 좋은 성능을 가졌지만, 정적 영역에 대해 비교적 아쉬운 성능을 확인했다.
위의 모델들이 생성한 장면들은 공통적으로 완벽하지 못하고 모션이 존재할 때 장면이 일그러지거나, 정적 영역에서 모션이 발생하여 일관된 장면을 복원하지 못하는 등, 왜곡되고 비현실적인 장면들이 생성되는 것을 확인할 수 있었다. 물론 모델을 통해서 특정 이미지에 대해 완벽에 가까운 결과를 만들어낼 수 있지만, 그것은 제한되고 통제적인 환경에서만 가능한 일이기에 아직 상용화 단계에 도달하기에는 불완전하다. 이러한 방법들의 한계점을 극복하기 위해, 동적 이미지 합성을 위한 4D Gaussian Splatting의 연구는 동적 영역 표현뿐만 아니라 정적 영역 표현 모두에 대해 범용적으로 좋은 성능을 내는 방향으로 연구되어야 할 것이다.
Acknowledgments
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. RS-2024-00414230, RS-2024-00456152).
References
-
Kerbl, B., Kopanas, G., Leimkühler, T., & Drettakis, G. “3D Gaussian Splatting for Real-Time Radiance Field Rendering,” ACM Transactions on Graphics, pp. 139:1-139:14, 2023.
[https://doi.org/10.1145/3592433]

-
Yang, Z., Gao, X., Zhou, W., Jiao, S., Zhang, Y., & Jin, X. “Deformable 3D Gaussians for High-Fidelity Monocular Dynamic Scene Reconstruction,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 20331-20341, 2024.
[https://doi.org/10.1109/cvpr52733.2024.01922]

-
Wu, G., Yi, T., Fang, J., Xie, L., Zhang, X., Wei, W., ... & Wang, X. “4D Gaussian Splatting for Real-Time Dynamic Scene Rendering,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 20310-20320, 2024.
[https://doi.org/10.1109/cvpr52733.2024.01920]

-
Huang, Y. H., Sun, Y. T., Yang, Z., Lyu, X., Cao, Y. P., & Qi, X. “SC-GS: Sparse-Controlled Gaussian Splatting for Editable Dynamic Scenes,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 4220-4230, 2024.
[https://doi.org/10.1109/cvpr52733.2024.00404]

-
Li, Z., Chen, Z., Li, Z., & Xu, Y. “Spacetime Gaussian Feature Splatting for Real-Time Dynamic View Synthesis,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 8508-8520, 2024.
[https://doi.org/10.1109/cvpr52733.2024.00813]

-
Wang, Z., Bovik, A. C., Sheikh, H. R., & Simoncelli, E. P. “Image Quality Assessment: From Error Visibility to Structural Similarity,” IEEE Transactions on Image Processing, vol. 13, no. 4, pp. 600-612, 2004.
[https://doi.org/10.1109/tip.2003.819861]

-
Teed, Z., & Deng, J. “RAFT: Recurrent All-Pairs Field Transforms for Optical Flow,” in Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part II 16, Springer International Publishing, pp. 402-419, 2020.
[https://doi.org/10.1007/978-3-030-58536-5_24]

-
Li, T., Lombardi, S., Sunkavalli, K., & Kholgade, N. “Neural 3D Video Synthesis from Multi-View Video,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 5521-5531, 2022.
[https://doi.org/10.1109/cvpr52688.2022.00544]


- 현재 : 부산대학교 전기전자공학부 전자공학전공
- ORCID : https://orcid.org/0009-0005-2040-9895
- 주관심분야 : 3D/4D Reconstruction, Diffusion models

- 현재 : 부경대학교 미디어커뮤니케이션학부 휴먼ICT융합전공 학사과정
- ORCID : https://orcid.org/0009-0008-9202-6510
- 주관심분야 : 3D/4D Reconstruction, Diffusion models

- 2012년 : 서울대학교 전기컴퓨터공학부 학사
- 2017년 : 서울대학교 전기정보공학부 박사
- 현재 : ETRI 실감미디어연구실 선임연구원
- ORCID : https://orcid.org/0000-0002-6470-0773
- 주관심분야 : Light field, VR/AR, 컴퓨터 비전

- 1999년 : 전북대학교 컴퓨터공학과 학사
- 2016년 : 경희대학교 전자전파공학회 박사
- 현재 : ETRI 실감미디어연구실 책임연구원
- ORCID : https://orcid.org/0009-0002-7574-2853
- 주관심분야 : VR/AR, Light Field, MPEG, 컴퓨터 비전

- 2015년 : 서강대학교 전자공학과 학사
- 2017년 : 포항공과대학교 전자전기공학과 석사
- 2020년 : 포항공과대학교 전자전기공학과 공학박사
- 2021년 : 포항공과대학교 전자전기공학과 박사후연구원
- 2023년 : 부경대학교 미디어커뮤니케이션학부 휴먼ICT융합전공 조교수
- 현재 : 부산대학교 전기전자공학부 전자공학전공 조교수
- ORCID : https://orcid.org/0000-0002-1135-7502
- 주관심분야 : 멀티미디어 영상신호처리, 컴퓨터 비전, 딥러닝 시스템 설계