Enhancing Image Compression with Foveal Vision: A Multi-Focus FPSNR Assessment and Attention-Based Neural Network
Copyright Ⓒ 2024 Korean Institute of Broadcast and Media Engineers. All rights reserved.
“This is an Open-Access article distributed under the terms of the Creative Commons BY-NC-ND (http://creativecommons.org/licenses/by-nc-nd/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited and not altered.”
Abstract
In the field of image and video compression, the objective is to achieve a balance between compression efficiency and the quality of reconstructed images. The commonly used quality assessment method in this field is the Peak Signal-to-Noise Ratio (PSNR), which, however, has a limitation in that it only considers the differences in pixel values. To address this, our research introduces the Foveal Peak Signal-to-Noise Ratio (F_PSNR), a visual perception-based approach that reflects human foveal vision. Specifically, we propose a multi-focus F_PSNR assessment method that incorporates the visual characteristics of humans for images containing multiple objects of interest. Additionally, we suggest a model that integrates an attention mechanism focusing on the quality of objects of interest into the existing neural network-based compression method to enhance perception-based quality. Experimental results using the KODAK dataset demonstrate that applying the attention mechanism to existing methods can enhance the human-perceptual compression efficiency of neural networks.
Keywords:
Foveation, Quality Assessment, Image Compression, Deep LearningⅠ. Introduction
The Human Visual System (HVS) is a complex system that enables us to see, process, distinguish, and recognize the environment around us. The visual perception of the human eye is characterized by varying resolution across different viewing angles, with high-resolution centres occurring in the area near the fixation point and decrease as one moves away from this fixation point[1]. Due to the uneven distribution of resolution in these fixation areas, the recognition of objects such as images often lacks sufficient detail[2]. In the field of image compression[3][4][5][6] comparison calculations are typically performed across the entire area rather than being focused on the fixation point, This approach ranges from the dominant to the less prominent, using the peak-signal-to-noise-ratio (PSNR) metric[7].
The fixation point is projected onto the fovea, which is the area with the highest sample density, and the entire resolution-changing data is referred to as a foveated image. By artificially creating a foveated image, low-frequency areas or those undetected in the original image are removed or disregarded, assuming a foveation point. The result is a foveated image that appears identical to the original image. In research conducted by S. Lee et al.[2][8][9] they projected the fixation area to be in the center of an object in the image, then calculated and compared that area based on the fovea factor and the same radius in the original image. On the other hand, L. Wang et al.[10] used foveated rendering techniques in super-resolution videos to enhance the super-resolution results at the fixation point. These methods represent substantial advancements in object detection and image quality enhancement at the fixation point. However, a significant challenge arises when images contain multiple objects with disparate fixation points. This situation requires advanced approaches to simultaneously manage multiple focal areas while maintaining image quality. The presence of multiple fixation points in an image highlights the necessity for research to refine foveated imaging techniques for complex visual contexts.
In this research, our aim is to develop the foveated region by increasing the fixation points on the image to enhance flexibility and improve accuracy in comparisons. This implies that the fixation points will have more than one Foveated-Peak-Signal-To-Noise-Ratio (F_PSNR) value within them. Additionally, we employ attention mechanisms[11] based on neural networks[3][11] to enhance compression and quality of the images obtained before calculations using the multi-foveated approach we created. Factors considered during this study include image quality and better compression efficiency. The incorporation of attention mechanisms is intended to focus the fixation points of the object on the reconstructed image. The nature of these attention mechanisms involves capturing dominant pixel values while disregarding less significant ones, effectively distinguishing objects from the background in the image. This mechanism facilitates concentration on images for testing using the evaluation metrics we developed, ultimately improving compression efficiency and image quality.
Ⅱ. Related Works
In this chapter, we will discuss previous research and other supporting references in the research we are conducting. In the previous chapter, several main references[7][8][10], have been explained, which serve as the main ideas in the development of the calculations we are conducting. As we know, PSNR is an evaluation metric used to measure the quality of image reconstruction results in comparison with the original image[7]. In its nature, this metric evaluates based on the peak value of the signal generated in the image and divides it by the Mean Square Error (MSE) obtained, as shown in equations (1) and (2). The higher the PSNR value obtained, the lower the level of noise generated. PSNR is measured in decibels (dB). However, this metric has limitations in its calculation because it only considers the differences in pixel values, which are taken as the final value of all existing pixels. Additionally, the calculation is not focused on objects or pixels that have dominant information values, so it cannot clearly determine whether important information in the image is in good condition or not. Therefore, the use of the foveal region is intended to focus the calculation and distribute it to areas that have dominant information values such as objects in the image shown in Figure 1, so that we can determine the quality of important information in pixels and ignore less relevant information values such as the background in the image.
| (1) |
| (2) |

Illustration of foveated images: (a) Kodim23.png[15], (b) single foveated regions, and (c) multiple foveated regions
In the process of calculating PSNR, the first step is to determine the value of Mean Square Error (MSE). Here, N represents the number of pixels in the image, Iref is the reference image to be compared with the reconstructed image Itest. Once the MSE is obtained, the next step is to calculate the PSNR using Equation (2), Max Pixel Value divided by the MSE.
In the study conducted by T.T. Huong et al[12], they examined the quality assessment of 360° images created using Graph Convolutional Neural Network (CNN) by calculating the PSNR values based on the fovea factor of the 360° images, with the assessment focusing on the obtained image objects. In the research by S. Lee et al[2], they analyzed foveated image and video data to demonstrate the effectiveness of their approach by simulating modified versions based on the H.263 model, resulting in improved efficiency and good quality of foveal images and compression. Furthermore, in another journal, S. Lee et al[8][9], also used the foveal factor to demonstrate adaptation to the foveal response in human vision, and the development of foveated video compression with optimal rate control. They introduced a non-uniform filtering scheme to match the non-uniform sampling of the human visual system (HVS), with a focus on maximizing the foveal signal-to-noise ratio (FSNR) to achieve high-quality video at low bit rates. In the research conducted by Agrawal, A et al[10], they took a different approach from several references explained earlier, wherein they combined the concepts of foveated rendering and traditional Super Resolution (SR) to produce high visual quality with low latency.
To evaluate the quality of a foveal object in the image, we employ a neural network image compression model approach using the Balle model[3]. We utilize this model to obtain and measure the reconstruction results in the image. Additionally, we incorporate the Attention block (AB)[11] to concentrate the reconstruction results in the fixation area during the testing process. According to T. Chen et al[13], adding attention mechanisms to the compression model allows it to capture non-local correlations more effectively and can enhance coding efficiency and compression. This is because the AB will prioritizes areas with dominant pixels and ignore areas with non-dominant pixels, thus focusing the results on the object areas in the image, which will later be evaluated using the foveal metric.
Inspired by several studies previously described, we introduce a multi-focus regions method that calculates fixation points in images using a multi-foveal approach. In the method we propose, this involves utilizing foveal factors and adjusting the image radius to determine the center point of objects for computation, as illustrated in Figure 1 kodim23.png (1a) in the Kodak dataset[14], which demonstrates the use of foveal in assessing object quality, single foveated in image (1b), and multi-foveated in image (1c). From the displayed illustration, it can be seen that the use of multi-foveated can assist in focusing calculations on regions containing more than one object, which is much better compared to using single foveal alone. From the illustration, the results show information in the image, namely two clearly defined bird objects, representing object values more accurately, thus obtaining more accurate information values.
Ⅲ. Methodology
In this section, we will discuss the method we developed based on previous research[8][10][12], as mentioned in the previous section. We added and focused on foveal regions with higher information values, as illustrated in Figure 1.
1. End-to-end Compression
The Ballé’s model[3] employs an variational autoencoder architecture with a generalized division normalization (GDN) layer, which is effective for simulating nonlinear transformation that have been frequently employed in subsequent approach[3][15][16]. this model incorporates a hyperprior to effectively capture spatial dependencies in the latent representation and to reduce reconstruction errors and data size, which opens new possibilities for neural network-based compression model. Base on the Balle model, we introduce an attention mechanism[11] to guide the compression model to focus on the foveal regions. As shown in Figure 2, the attention block (AB) is integrated into the Balle’s model, added after the encoding process and before the decoding process. This placement ensures that the attention mechanism makes has an effect on both compressed features and features to be reconstructed.
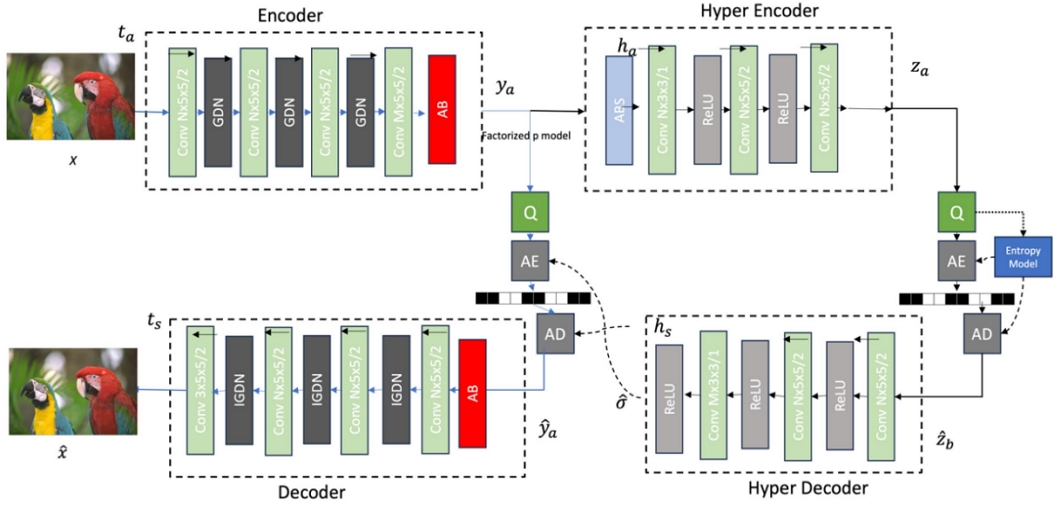
The compression model is divided into two parts: the left side is the variational autoencoder, and the right side is the hyperprior. The symbols ta and ts represent the analysis and synthesis transforms. Q is quantization. AE and AD represent arithmetic encoding and decoding, ha and hs is hyper parameter. The arrow symbols represent up-sampling ↑, and down-sampling ↓ operations. The AB stands for the attention block.
Initially, the original image x is passed through the main encoder network, creating the corresponding latent representation ya using four convolutional layers with the non-linear function GDN. Afterward, ya is quantized into the quantized latent form ya is then passed to the decoder network to generate the final reconstructed image after arithmetic encoding (AE) and decoding (AD)[17]. Similarly, we utilize the same quantization method as[3][15] with some modifications to the end of the encoder and the beginning of the decoder by adding the (AB) block. This method of entropy coding uses a hyperprior network to produce an estimate of the latent form before quantization and encoding the output of the hyperprior encoder into the bitstream. It will be encoded into the bitstream because this information is necessary for decoding, and the proper entropy model will increase compression effectiveness. In this study, the hyper-encoder module receives information from ya and encodes it into the latent representation za. Then it is quantized into and passed to the hyper-decoder module after the AE and AD process. The Hyper-decoder module again retrieves hyperprior information from and estimates relevant entropy model parameters φ, ϑ.
Below is Equation (3) for the loss function used to optimize the entire training process of the compression technique. In the first equation, D represents distortion, and E represents bitrate. The factor λ (lambda) considers the trade-off between distortion and bitrate. Distortion is measured using the Multi-Structural Similarity Index Measure (MS-SSIM)[18], which is used to assess the visual quality of an image by considering the structural similarity between the original image x and the reconstructed image x, denoted by d(⋅). It involves the bitrates and , which are used to encode the visualizations of their respective output values.
| (3) |
In addition to the training process, we use the entropy estimation method shown in [6] and formulate it in the following equation (4).
| (4) |
Each latent representation is modeled as a Gaussian distribution characterized by the parameters φi and ϑi, predicted by the probability of the hidden element . The term is known as the hyperprior. The symbol denotes a uniform distribution, while *represents the convolution operation. The hyperprior is described in equation (5) as follows:
| (5) |
In this context, each distribution is represented by and its parameters are denoted by ψ(i). The bit rate in our technique comprises the bitrate for the hidden variable and the latent representation . However, the bits from equation (3) can be represented as follows:
| (6) |
| (7) |
The training of the model aims to achieve compression efficiency and enhance the quality of images. This model is trained with 500 epochs, 500 steps per epoch, λ with a range from 0.01 to 1.0, batch size equal to 8, and learning rate equal to 1e-4. The CLIC dataset[19] is utilized for training and validation, and the KODAK dataset[14] is used for testing.
2. Multi-Foveated Focuses
The first step taken to measure the uality of foveal regions is to divide an image into multiple regions, which can be represented as either the foreground region Φj (l≤j≤Nf), and the peripheral region Φ0, as illustrated in Figure 3(a). Nf is the total number of the foreground regions. We took a different approach from previous references in determining the foveal regions[8]. After the separation, Φj region with center points cj, (xcj,ycj) are obtained. The next step is to search for the mask of each region to focus the calculation in the foveal regions rather than the peripheral regions. The foveal mask MΦj of the regions Φj has 1 inside the region Φj and 0 outside of the region Φj.
| (8) |
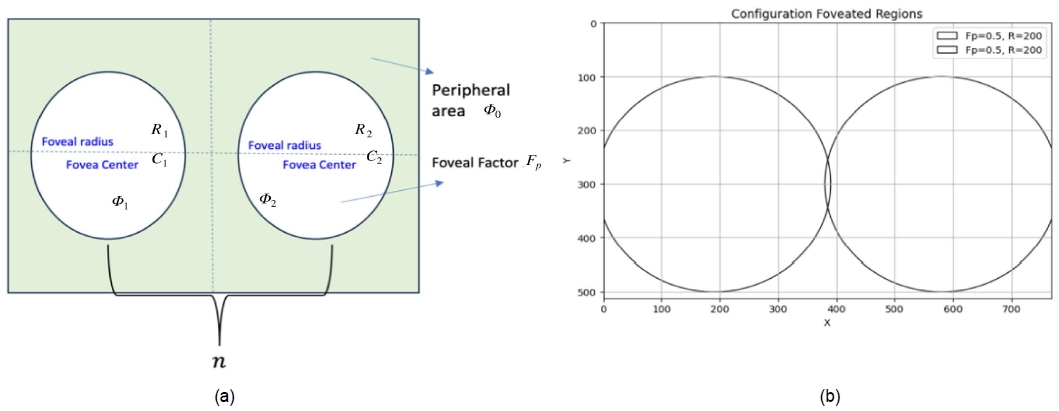
Configuration of foveated regions based on a resolution of 768 ×512 on the KODAK dataset, Image (a) on the left represents part of the Foveated Region, (b) while the second image represents the results obtained during testing. The Fp value represents the foveal factor used, and R represents the Foveal Radius from the center point on the Fp object which adjusts to the resolution.
After the mask regions is determined, MSE is computed only for the pixels in the region Φj, regardless of the pixels outside this region using equation (8). This is denoted by F_MSE(Φj). In this equation, Iref(i) and Itest(i) represents the i-th pixel value of the reference image and the test image, respectively. N is the total number of pixels in the test image. Meanwhile, the value in F_MSE(Φj) is the MSE result of Φj, where MΦj(i)indicates the mask for the i-th pixel.
| (9) |
PSNR of the region Φj, F_PSNR(Φj), is measured using equation (9). This equation will focus the calculation only on the foveal region. This equation can be also used if there is only one foveal point, as done by [8]. If the number of foveal regions is more than one, average quality of all foveal regions is obtained by equation (10).
| (10) |
where is mean of F_PSNR(Φj) for all foveal regions. This equation can be applied to images with multiple foveal regions, as shown in Figure 3.
The final step is to evaluate the image quality by differentially considering the quality of the foreground and peripheral regions. The proposed image quality measure is M-FPSNR, as described in equation (11).
| (11) |
where, Fp represents the foveal factor used to weight foveal and peripheral regions. F_PSNR(Φ0) is PNSR of the peripheral regions. M-FPSNR aims to provide a more accurate assessment, focusing on foreground regions. Fp allows for adjusting how much the quality of the foveal regions is prioritized over the quality of the peripheral region.
3. Attention Block
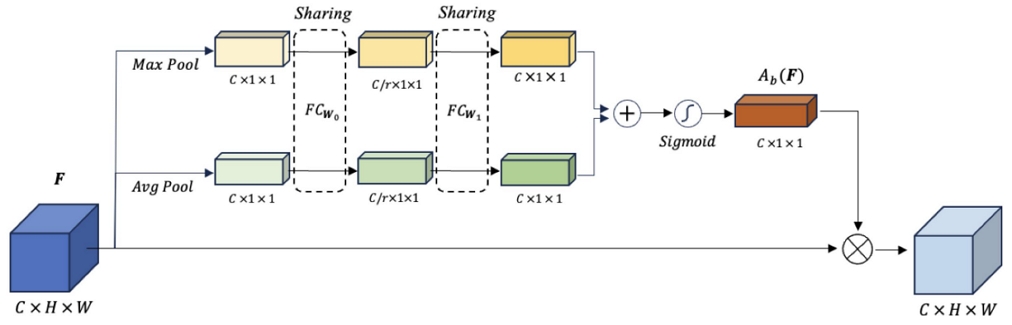
Figure 4 illustrates the attention block designed to enable the compression neural network to incorporate the foveated focus regions. The process of deriving the channel attention, Ab(F), for element-wise multiplication with an input feature, F, is formulated in Equation (12).
| (12) |
First, both average pooling, Avgpool(F), and max pooling, MaxPool(F), are concurrently applied to gather spatial information from an input feature map. Subsequently, both pooled feature vectors are directed to shared fully connected layers, FCW0 and FCW1. FCW0 and FCW1 are used to perform linear transformations on the pooled feature vectors. By sharing weights in FCW0 and FCW1, the layers learn to extract more general features from the data without increasing the number of parameters too much. The size of the first fully connected layer, FCW0, is defined as , with r representing the reduction ratio employed to reduce parameter overhead. In this paper, we set r to 64. The size of the second fully connected layer is configured as , aligning with the dimensionality of the pooled feature vectors. Thus, the weighting parameters are defined as W0 and W1 are shared for both pooled feature vectors. The ReLU activation function is used for the fully connected layers. Following the shared fully connected layers, the resulting output feature vectors are merged using element-wise summation and the sigmoid activation function σ.
Ⅳ. Experiment Results
In this stage, we evaluate the overall results obtained during training and testing. The results show the performance of bits per pixel (BPP) and quality assessment, as indicated in Table 1. Based on these findings, the Multi-Foveated M-FPSNR we obtained outperforms the Single Focus Foveated F_PSNR in equation (9) and regular PSNR. Additionally, the attention prioritizes information on the objects rather than the background. With the presence of dominant pixels, the resulting image focuses on the object rather than the background. If only regular PSNR is used, the value taken will be the overall pixel in the image, resulting in the final value not representing dominant information but rather the average of all pixels. However, using foveated factor calculations will focus on regions with more important information than the background of the object.
In Table 1, the test results using the neural network model[3] reveal that M-FPSNR values have an advantage in calculating differences between pixels of reconstructed objects by employing more than one foveal factor. Additionally, the utilization of attention mechanisms enables a more detailed focus on object areas compared to not using attention mechanisms. This leads to slightly improved metric evaluation values for each tested lambda.
We tested various values of the foveal factor FP in the range of 0.0 to 0.5 based on Equation (11). This testing aimed to determine which FP value performs better throughout the experiment. In Table 2, the comparison results of the images are based on the output PSNR of the Balle’s model[3], by dividing the results from M-FPSNR/PSNR From these results it can be seen that weighting the value on FP has a significant impact on the improvement of image quality. The highest value is obtained at a lambda of 0.80, with an average improvement of 13.159% compared to Ballé’s, which is better to regular PSNR. Additionally, the improvement in the obtained image results continues to increase with the lambda values used. This occurs because the foveal factor value used focuses the calculation solely on the foveal regions, resulting in a comparison value between the original image and the reconstructed image within that region. In testing FP equal to 0.0, the results obtained are better compared to other values. This happens because the image quality is measured only for the foveal regions regardless the quality of the peripheral region. The FP of 0.0 only focuses on Φj while FP of other values considers both foveal and peripheral regions with different priorities.
According various image quality metrics, the utilization of the attention block is tested compared to the Ballé’s model[3] not employing the attention mechanism. As shown in Table 3 and Figure 5. The incorporation of attention mechanisms significantly enhances coding efficiency compared to the Ballé’s model, achieving an average of -12.73% BD-rate under the PSNR metric, an average of -13.98% BD-rate under the F_PSNR metric, and an average of -15.91% BD-rate under the M-FPSNR metric. Evaluation metrics using the foveal factor can assess reconstructed images by considering the specific importance of individual objects within the image, whereas PSNR evaluates the overall image quality without assigning such importance.

Qualitative comparison results using the Kodak dataset between original data and using AB. Kodim 23.png Left: Original, Middle: Balle 2018, Right: ours.
In Table 3, the results of the image quality metric calculations using the Kodak dataset are presented. These results were obtained through testing and comparing the quality metrics we developed with other metrics. The testing metric was conducted using different foveal factors ranging from 0.0 to 0.5 for F_PSNR and M-FPSNR. Based on these calculations, the values of PSNR, F_PSNR, and M-FPSNR were determined. Our M-FPSNR metric is capable of calculating regions in the image more accurately compared to other calculation metrics[7][8]. This is due to the use of multi-foveated focusing on more than one object in the reconstructed image, and the utilization of foveated regions set based on points on the object in each image, which can concentrate the calculations. The foveal factor value used for the results in Table 3 is 0.5. This value was chosen based on the object regions in the Kodak dataset we used. The more changes in an object, the more it will affect the selected foveal factor value. The PSNR value shows poorer results compared to both metrics, as PSNR calculates the entire area without considering areas affected by noise or not, thus impacting the final received value.
1. Qualitative Results
In Figure 5, the results of comparative visualization are presented to clarify the approach we have taken. From the image, a qualitative comparison can be seen between the original image, the results from balle[3], and the method we propose. We highlight specific areas in the reconstructed image kodim23.png for detailed examination. The results we propose show much more detailed image quality that closely approaches the original image. Furthermore, the use of AB can enhance the texture in the image, particularly in dominant objects, while also maintaining a more efficient bitrate, as demonstrated in Figure 6.
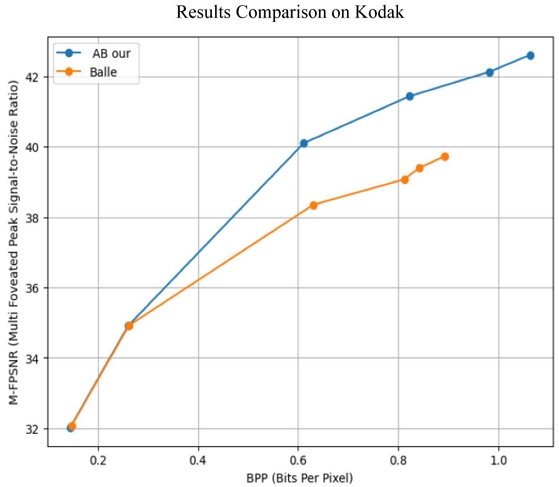
Comparison rate (BD-rate) and distortion (M-FPSNR) curve between Balle model[3] and our method with attention block
Furthermore, as mentioned at the beginning of the chapter, the nature of AB tends to prioritize important information and disregard less important information, such as objects in the image. AB will prioritize information on the dominant objects in the image compared to their background, which contains minimal information. Therefore, the use of PSNR is less effective in assessing the quality of the reconstruction results obtained with AB. On the other hand, the M-FPSNR metric we developed is capable of calculating the area from the reconstruction results obtained with AB.
In the graph shown in Figure 6, it can be seen that the AB value exhibits better coding efficiency compared to the Balle model. This is attributed to the nature of AB, which adaptively emphasizes important information from each channel of the resulting feature. Several factors contribute to the increase in coding efficiency, including reducing the dimensions of irrelevant features by paying greater attention to the dominant feature channels, the model can reduce the dimensions of irrelevant features or noise, in addition to increasing representational information it can produce more informative and discriminative features, and finally, context adaptation where the model allows adaptation to changes in task input. In Figure 6, there seems to be minimal difference in performance observed at low bitrates, which can be attributed to inherent limitations in compression algorithms. At lower bitrates, the compression process tends to prioritize retaining important image details while sacrificing less critical information. Consequently, this may lead to a convergence in performance among various techniques, as models struggle to maintain quality under severe compression constraints. The AB block used only captures dominant pixels at low bitrate. Additionally, factors such as noise and artifacts become more pronounced at lower bitrates, further obscuring performance differences.
Therefore, the placement of AB within the model can affect the increase in coding efficiency obtained. In the research we conducted, AB was positioned at the end of the encoder and at the beginning of the decoder, producing output Ab(F). This output will be passed into the hyperparameters to enhance the results in the hyperprior and reconstruction stages in the decoder section. This placement is chosen so that the AB block can understand the input context as a whole, as well as reduce irrelevant or redundant features. Furthermore, it provides flexibility for the model to adjust attention for image compression tasks. Meanwhile, placing it before the decoder aims to facilitate reconstruction to help produce more accurate output, as well as improve the overall model performance.
Ⅴ. Conclusion
In this paper, we introduce a novel image quality assessment method that supports multiple fixation areas characterized by object coordinates and the human visual system's foveal response. We also employ a neural network inspired by Balle’s model, enhancing it with an attention mechanism to improve accuracy in reconstructing and evaluating image quality, specifically through M-FPSNR. Our findings demonstrate that our M-FPSNR metric outperforms several current evaluation methods, with optimal performance at lambda 0.80, showing a 13.159% improvement. This advancement indicates superior compression efficiency and image quality, evidenced by notable BD-Rate improvements for PSNR, F_PSNR, and M-FPSNR metrics. Our work represents a potential breakthrough in multimedia and image compression, setting the stage for future research in visual quality assessment through innovative approaches like object-focused segmentation, aiming to surpass the accuracy of traditional methods.
Acknowledgments
This work was supported by Instittute of Information & communications Technology Planning & Evaluation (ITTP) grant funded by the Korea goverment (MSIT) (No.RS-2023-00227431, Development of 3D space digital media standard technology)
References
-
M. Paul and M. Musfequs Salehin, “Spatial and motion saliency prediction method using eye tracker data for video summarization,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 29, no. 6, pp. 1856-1867, June 2019.
[https://doi.org/10.1109/TCSVT.2018.2844780]

-
S. Lee and A. C. Bovik, “Foveated video image analysis and compression gain measurements,” 4th IEEE Southwest Symposium on Image Analysis and Interpretation, Austin, TX, USA, 2000, pp. 63-67,
[https://doi.org/10.1109/IAI.2000.839572]

-
J. Ballé, D. Minnen, S. Singh, S. J. Hwang, and N. Johnston, “Variational image compression with a scale hyperprior,” 6th International Conference on Learning Representations, ICLR 2018 - Conference Track Proceedings, 2018.
[https://doi.org/10.48550/arXiv.1802.01436]

- S. A. Wilson and A. A. Farag, “Image compression using neural networks,” Intelligent Engineering Systems Through Artificial Neural Networks, vol. 5, pp. 503–508, 1995.
- M. Al-Ani, F. H. Awad, M. Shaban AL-Ani, and F. Hammadi Awad, “The JPEG Image Compression Algorithm,” Int J Adv Eng Technol, vol. 6, no. 3, pp. 1055–1062, 2013, [Online]. Available: https://www.researchgate.net/publication/268523100
-
Li W, Sun W, Zhao Y, Yuan Z, Liu Y, “Deep image compression with residual learning,” Applied Sciences (Switzerland), vol. 10, no. 11, pp. 1–13, 2020.
[https://doi.org/10.3390/app10114023]

-
A. Horé and D. Ziou, “Image Quality Metrics: PSNR vs. SSIM,” 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 2010, pp. 2366-2369,
[https://doi.org/10.1109/ICPR.2010.579]

-
S. Lee, M. S. Pattichis, and A. C. Bovik, “Foveated video quality assessment,” IEEE Trans Multimedia, vol. 4, no. 1, pp. 129–132, 2002.
[https://doi.org/10.1109/6046.985561]

-
Lee S, Pattichis MS, Bovik AC. Foveated video compression with optimal rate control. IEEE Trans Image Process. 2001;10(7):977-92. PMID:18249671
[https://doi.org/10.1109/83.931092]

-
L. Wang, M. Hajiesmaili, and R. K. Sitaraman, “FOCAS: Practical Video Super Resolution using Foveated Rendering,” MM 2021 -– Proceeding International Conference on Multimedia, Us of the 29th ACM SA. pp. 5454–5462, 2021.
[https://doi.org/10.1145/3474085.3475673]

-
S. Woo, J. Park, J. Y. Lee, and I. S. Kweon, “CBAM: Convolutional block attention module,” In Computer Vision – ECCV 2018: 15th European Conference, Munich, Germany, September 8–14, 2018, Proceedings, Part VII. Springer-Verlag, Berlin, Heidelberg, 3–19.
[https://doi.org/10.1007/978-3-030-01234-2_1]

-
T. T. Huong et al., “An Effective Foveated 360° Image Assessment Based on Graph Convolution Network,” IEEE Access, vol. 10, no., pp. 98165–98178, 2022.
[https://doi.org/10.1109/ACCESS.2022.3204766]

-
T. Chen, H. Liu, Z. Ma, Q. Shen, X. Cao, and Y. Wang, “End-to-End Learnt Image Compression via Non-Local Attention Optimization and Improved Context Modeling,” IEEE Transactions on Image Processing, vol. 30, pp. 3179–3191, 2021.
[https://doi.org/10.1109/TIP.2021.3058615]

-
V. N. V. Satya Prakash, K. Satya Prasad, and T. Jaya Chandra Prasad, “Color image demosaicing using sparse based radial basis function network,” Alexandria Engineering Journal, vol. 56, no. 4, pp. 477–483, Dec. 2017.
[https://doi.org/10.1016/j.aej.2016.08.032]

-
D. Minnen, J. Ballé, and G. Toderici, “Joint autoregressive and hierarchical priors for learned image compression,” Adv Neural Inf Process Syst, vol. 2018-Decem, no. Nips, pp. 10771–10780, 2018.
[https://doi.org/10.48550/arXiv.1809.02736]

-
J. Ballé, V. Laparra, and E. P. Simoncelli, “End-to-end optimized image compression,” 5th International Conference on Learning Representations, ICLR 2017 - Conference Track Proceedings, 2017.
[https://doi.org/10.48550/arXiv.1611.01704]

-
E. H. Sibley, I. A. N. H. Willen, R. M. Neal, and J. G. Cleary, “Arithmetic Coding For Data Compression” Communications of the ACM 0001-0782/87/0600-0520 75 vol. 30, no. 6, 1987.
[https://doi.org/10.1145/214762.214771]

-
Z. Wang, E. P. Simoncelli and A. C. Bovik, “Multiscale structural similarity for image quality assessment,” The Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, pp. 1398-1402, Vol.2, 2003
[https://doi.org/10.1109/ACSSC.2003.1292216]

- “CLIC.” [Online]. Available: http://www.compression.cc, G. Toderici, W.Shi, R. Timofte, L. Theis, J. Balle, E. Agustsson, N. Jhonston, and F. Mentzer, “Workshop and Challenge on Learned Image Compression (CLIC2020),” CVPR, 2020. [Online]. Available: https://www.compression.cc, (Accessed: Aug. 21, 2024).

- 2017 : Bachelor of Electrical Engineering, General Achmad Yani University
- 2019 : Master of Electrical Enginerring, Telkom University
- Present : Ph.D candidate Intelligence Media engineering, Hanbat Nnational University
- ORCID : https://orcid.org/0000-0002-4068-174X
- Research interests : Image Processing, Deep Learning, Networking, Machine Learning

- 1997 : Bachelor of Science in Electronics Engineering, Kyungpook National University
- 1999 : Master of Science in Electrical Engineering, Korea Advanced Institute of Science and Technology
- 2004 : Ph.D in Electrical Engineering, Korea Advanced Institute of Science and Technology
- 2010 ~ Present : Professor, Department of Intelligence Media Engineering, Hanbat National University
- ORCID : https://orcid.org/0000-0002-7594-0828
- Research interests : Image Processing, Video Coding, Computer Vision