셀룰러 재난문자 방송을 위한 강화학습 기반의 동시 경보 메시지


Copyright © 2024 Korean Institute of Broadcast and Media Engineers. All rights reserved.
“This is an Open-Access article distributed under the terms of the Creative Commons BY-NC-ND (http://creativecommons.org/licenses/by-nc-nd/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited and not altered.”
초록
3GPP 표준은 CBS 방송 기반의 재난문자 서비스에서 동시 경보 메시지를 규정한다. 그러나 동시 경보 메시지의 개별적인 재전송 횟수를 결정하는 방식을 규정하고 있지 않다. 수신 성공률을 최대화하기 위해 각 지역에 동시 전송되는 경보 메시지의 개별적인 재전송 횟수를 결정해야 한다. 이를 위해 본 논문에서는 CBS 방송 기반의 재난문자 서비스를 위하여 강화학습을 이용하는 동시 경보 메시지 기법을 제안한다. 제안된 강화학습은 개별 재전송 횟수를 효과적으로 결정하며 모의실험은 제안된 기법의 우수한 성능을 보인다.
Abstract
The 3GPP standard specifies the concurrent warning message for cell broadcast service. However, it does not specify how to determine the number of re-transmissions for each message. To maximize the success rate of reception, it is required to determine the number of re-transmissions for each region-specific warning message. This paper addresses a reinforcement learning technique to determine the number for the concurrent warning message. Simulation results exhibit the excellent performance of the proposed approach.
Keywords:
Cell Broadcast Service, Concurrent Warning Message, Reinforcement LearningⅠ. 서 론
셀룰러 기반 재난문자 서비스인 CBS(Cell Broadcast Service)의 3GPP 표준은 동시 경보 메시지인 CWM(Concurrent Warning Message)을 규정한다[1]. 특히 동일 셀 안에 다른 지역에서 서로 다른 재난이 동시에 발생하는 경우 기지국은 CWM을 이용하여 각기 다른 경보 메시지를 각 지역으로 방송할 수 있다[2]. 또한 3GPP는 경보 메시지의 수신율을 높이기 위하여 재전송을 규정하며 CBS는 재전송 총횟수를 결정할 수 있다[1].
그러나 현 3GPP 표준은 서로 다른 CWM 메시지를 위한 개별 재전송 횟수를 규정하고 있지 않다. 따라서 기존 재전송 방식은 CWM 메시지의 전송 지역과 관계없이 메시지 별 같은 재전송 횟수를 사용할 수 있다. 그러나 CWM 메시지는 각각 다른 지역으로 전송되므로 메시지 별 같은 재전송 횟수는 최적의 수신 성공률을 보장하지 못한다. 이를 극복하기 위하여 본 논문에서 강화학습 기반의 CWM 기법을 제안한다. 즉 강화학습을 이용하여 지역별 CWM 메시지를 위한 최적 재전송 횟수를 찾는다. 이 최적 재전송 횟수는 최적 수신 성공률을 보장한다. 강화학습 기법으로 Q-학습을 이용한다[3]. 기존의 Q-학습과 달리 제안된 기법은 상태(state), 행동(action) 외에 지역 위치정보를 이용한다. 또한 Q-학습이 사용하는 보상(reward)으로 수신 성공률을 이용한다. 이 수신 성공률은 지역 위치정보와 연계된다[4]. 연속적인 지역 위치정보에 대응하기 위하여 딥(deep) MLP(Multi-Layer Perceptron)를 이용한다[5]. 즉 딥 MLP는 현 상태와 지역 위치정보를 입력으로 하여 각 행동의 가치(value)를 결정한다. 기존 딥 강화학습[6]과는 달리 Q-학습만으로 얻은 가치함수(value function)를 이용하여 딥 MLP를 학습한다. 기존 딥 강화학습은 딥 MLP를 이용하여 다음 상태의 가치함수를 구한다.
모의실험은 제안된 강화학습 기법이 CWM의 최적 재전송 성능에 도달함을 보이며 우수한 수신 성공률과 실용성을 입증한다.
Ⅱ. 동시 경보 메시지를 위한 강화학습 기법
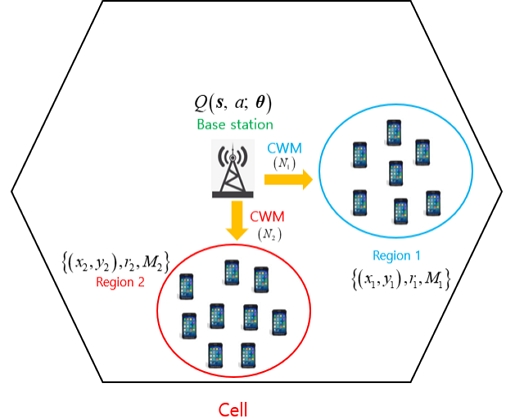
그림 1은 기지국이 셀 안의 2개 지역에 각각 다른 CBS용 동시 경보 메시지 CWM을 전달하는 예를 보여준다. 그림 1에서 지역 i (i = 1, 2)는 중심 위치 (xi, yi)와 반지름 ri로 결정된다[2]. 이 경우 보상 rwd(N1, N2;θ)는 다음 수신 성공률로 정의된다:
| (1) |
식 (1)에서 pe,i는 지역 1 또는 지역 2에 위치한 단말기 i의 수신 실패율이며 지역 위치정보 θ와 연계된다[4]. 그리고 M1과 M2는 지역 1과 지역 2에 위치한 단말기 개수이다. 또한 지역 위치정보 θ는 다음과 같이 정의된다:
| (2) |
식 (1)에서 N1과 N2는 지역 1과 지역 2의 재전송 횟수이며 다음과 같이 제한된다:
| (3) |
이 식에서 Ntot는 CBS 시스템이 허용하는 재전송 총횟수이다.
강화학습인 Q-학습은 식 (1)을 이용하여 상태-행동-위치정보 가치함수 Q(s, a;θ)를 구한다:
| (4) |
여기서 s는 현 상태 s = {N1, N2}를 의미하며 s'는 다음 상태 s' = {N1', N2'}를 가리킨다. 식 (4)에서 ρ와 γ는 학습률과 할인율을 가리킨다. 식 (4)는 Q-학습에서 이용되는 Bellman equation[3]을 기반으로 한다. 또한 현 상태 s에서 행동 a는 행동 1과 행동 2에서 선택되며 다음과 같이 정의된다:
| (5) |
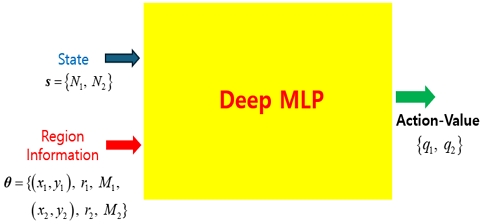
그리고 다음 상태 s'에서 행동 a' 또한 식 (5)로 정의된다. 식 (4)의 가치함수는 기존 Q-학습과 달리 연속 정보로 구성된 지역 위치정보를 포함한다. 따라서 연속 정보를 입력으로 이용할 수 있는 딥 MLP를 이용한다. 그림 2는 제안된 강화학습을 위한 딥 MLP를 보여준다. 이 딥 MLP는 강화학습을 위하여 입력층, 다수의 은닉층, 출력층으로 구성된다[6]. 사용되는 딥 MPL는 현 상태 s와 지역 위치정보 θ를 입력으로 하여 행동 1과 행동 2의 가치값 {q1, q2}를 출력한다. 즉 딥 MLP의 입력층은 2개의 현 상태(N1, N2)와 8개의 지역 정보(x1, y1, r1, M1, x2, y2, r2, M2)를 이용하며 출력층은 2개의 출력값 (q1, q2)을 생성한다. 그림 2의 딥 MLP는 기존 딥 강화학습과는 달리 입력으로 사용되는 현 상태 s가 이산값이며 다음 상태 s'의 가치함수 Q(s', a';θ)를 출력하지 않는다. 즉 (4)의 Q-학습만으로 얻은 가치함수를 타겟값으로 사용하여 딥 MLP를 학습한다. 강화학습 기반의 CWM 기법은 학습된 딥 MLP로부터 최대 가치값에 대응하는 행동을 선택하여 다음 상태 s'로 이동한다. 즉 (3)의 조건에서 재전송 횟수를 증가시키면서 최종 상태에 도달한다.
제안된 강화학습을 위한 가치함수와 딥 MLP의 학습 알고리즘을 아래 기술한다:
III. 모의실험
표 1은 모의실험을 위한 파라미터들을 보여준다. 셀 안의 각 CWM 지역에는 100개의 휴대 단말기가 균일분포에 따라 위치한다. 지역 반경은 50m이며, 중심 위치는 (-350, -350)부터 (350, 350)의 범위에서 균일분포에 따라 무작위로 선택된다. 또한 Q-학습을 위한 학습률과 할인율은 각각 0.9, 0.99이다. 모의실험에서 사용된 무선 채널은 레일리 (Rayleigh) 페이딩과 단순 경로 손실(simplified path loss) 모델이다[4]. CBS의 재전송 총횟수(Ntot)는 12이다.
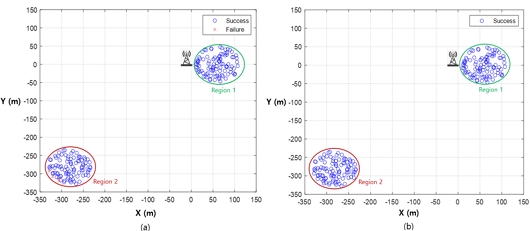
그림 3은 기존 재전송 방식과 강화학습 기반 재전송 방식의 경우 수신성공과 수신실패 예를 비교한다. 기지국에서 CWM용 지역 1과 지역 2 중심은 각각 60m, 300m의 거리에 위치한다. 그림 3 (a)는 기존 재전송 방식으로 각 지역의 재전송 횟수는 균일하게 6이 된다. 이 경우 지역 2의 4개 단말기가 재난문자 수신에 최종 실패한다. 그림 3 (b)는 강화학습을 이용한 경우로 지역 1과 지역 2의 재전송 횟수는 각각 1, 11이다. 그림 3 (b)는 지역 1과 2의 모든 단말기가 재난문자 수신에 최종 성공했음을 보여준다.
표 2는 1000번의 실험에서 각 재전송 방식을 이용하여 재난문자 수신에 최종 실패한 단말기의 평균 개수를 비교한다. 최적 방식은 수신 성공률이 최대가 되는 CWM 지역 재전송 최적 횟수를 오프라인에서 수치해석으로 구하였다. 오프라인에서 사용되는 이 최적 방식은 실제 CBS 시스템에 적용할 수 없다. 제안된 강화학습 방식과 최적 방식은 평균 0.1의 수신실패 단말기 수를 보여준다. 즉 제안된 방식의 성능은 최적 방식의 성능에 도달하며 수신에 실패한 단말기의 수는 0에 가깝다. 그러나 기존 방식으로는 평균 3.6개의 단말기가 재난문자 수신에 최종 실패한다.
Ⅳ. 결 론
CBS 동시 경보 메시지의 수신 성공률을 극대화하기 위하여 Q-학습과 딥 MLP를 이용하는 강화학습 기반의 재전송 방식을 제안하였다. 이 방식은 CWM의 최적 재전송 성능에 도달하며 우수한 수신 성공률과 실용성을 보였다. 본 연구의 주요 성과로 CWM의 최적 재전송 성능을 얻을 수 있는 강화학습 기법을 확보하였으며, 실제 CBS 시스템에 적용 가능한 의의를 가진다. 현 연구내용은 고정된 재전송 총횟수(Ntot)를 사용한다. 향후 이 재전송 총횟수를 최소화하는 방법을 연구할 예정이다.
Acknowledgments
이 논문은 2024년도 서울시립대학교 교내학술연구비에 의하여 지원되었음.
This work was supported by the 2024 Research Fund of the University of Seoul.
References
- 3GPP TS 23.041: Technical Realization of Cell Broadcast Service (CBS), 2022. https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=748
- ATIS-0700041, Wireless Emergency Alerts (WEA) 3.0: Device-Based Geo-Fencing, 2019. https://webstore.ansi.org/standards/atis/atis0700041?srsltid=AfmBOoqzBZKBYb2gqFyOcC2LcvhJuytnmpYw8GK2ci6F0qg2GDvHUkVw
-
C.-M. Wu, C.-T. Tsai, C.-C. Hou, J.-J. Yang, G.-D. Lin, and M.-Y. Kuang, “Emergency message broadcast mechanism in vehicular ad-hoc networks based on reinforcement learning with contention estimation,” IEEE Trans. Intelligent Vehicles (Early Access), 2024.
[https://doi.org/10.1109/TIV.2024.3418778]

- A. Goldsmith, Wireless Communications, Cambridge University Press, 2005. https://www.cambridge.org/core/books/wireless-communications/800BA8A8211FBECB133A7BB77CD2E2BD
- I. Goodfellow, Y. Bengio, and A. Courville, Deep Learning, The MIT Press, 2016. https://www.deeplearningbook.org/
-
X. Wang, S. Wang, X. Liang, D. Zhao, J. Huang, X. Xu, B. Dai, and Q. Miao, “Deep reinforcement learning: a survey,” IEEE Trans. Neural Networks and Learning Systems, vol. 35, no. 4, Apr. 2024.
[https://doi.org/10.1109/TNNLS.2022.3207346]