
Neural Light Field 뷰 합성 성능 예측에 효과적인 이미지 복잡도 평가지표에 관한 연구
Copyright © 2024 Korean Institute of Broadcast and Media Engineers. All rights reserved.
“This is an Open-Access article distributed under the terms of the Creative Commons BY-NC-ND (http://creativecommons.org/licenses/by-nc-nd/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited and not altered.”
초록
Neural Light Field (NeLF)는 Implicit representation과 Light ray의 색상 정보의 관계를 학습하고, 이를 바탕으로 대상 공간 또는 물체를 재구성하는 기술로, 우수한 성능을 바탕으로 활발히 최근 연구되고 있다. NeLF는 학습하고자 하는 대상 공간, 물체의 복잡도에 따라 학습성능이 달라지는데, 복잡한 공간의 경우 낮은 Peak Signal-to-noise ratio (PSNR)의 성능을, 단조로운 공간의 경우 높은 PSNR 결과를 보인다. 이러한 경향과 별개로, 학습이 진행되기 이전에는 어느 정도 수준의 PSNR이 예측될지는 알기 어려우며, 실제로 학습이 이루어져야 확인이 가능하다. 본 논문은 NeLF 학습에 사용되는 이미지를 바탕으로 해당 공간의 학습성능을 예측하기 위한 연구를 수행하며, 특히 NeLF 학습성능 예측에 효과적인 이미지 복잡도 평가지표에 관해 연구한다. 본 논문은 이미지 복잡도 평가에 사용되는 6가지 평가지표를 선정, 실제 학습한 PSNR 결과와 해당 평가지표 사이의 관계를 분석한다. 실험에서는 NeLF 연구에서 주로 사용되는 데이터 샘플에 추가적으로 직접 촬영한 샘플을 포함 총 30개의 샘플을 통해 NeLF 학습성능과 가장 관련성이 높은 평가지표를 선정하며, 테스트용 샘플 5개에 대한 PSNR 예측하고 이를 분석한다.
Abstract
Neural Light Field (NeLF) is an approach that learns the relationship between implicit representations and the color information of light rays, using this knowledge to reconstruct real spaces or objects. NeLF has been actively researched recently due to its impressive performance. However, the training performance of NeLF varies depending on the complexity of the target space or object. In general, the training performance of NeLF for complex spaces is low, and for simple spaces it is high. Regardless of this trend, it is difficult to predict the level of PSNR before training. This paper studies methods to predict the training performance of NeLF based on the images used for training, and in particular studies image complexity metrics that are effective in predicting NeLF training performance. This paper selects six evaluation metrics used to assess image complexity and analyzes the relationship between the actual PSNR results and the corresponding complexity. The experiment is based on a total of 30 samples, including standard data samples commonly used in NeLF research as well as samples directly captured for this study, to explore the most relevant image complexity metrics for NeLF performance. The experiment also predicts PSNR for five test samples and analyzes the prediction errors.
Keywords:
Light Field, Neural Light Field, Image Complexity, Novel View SynthesisⅠ. 서 론
자유로운 시점에서의 다양한 뷰를 합성하는 novel view synthesis는 실제로 취득한 이미지들로부터 취득하지 않은 임의의 위치에서의 뷰를 합성하는 기술로, 가상현실(Virtual Reality)과 증강현실(Augmented Reality)에서 필수적인 기술에 해당된다. 전통적으로는 촬영한 여러 장의 이미지로부터 포인트 클라우드를 추정하고, 메쉬(Mesh)를 생성하는 3차원 모델링 방법[1,2]과, 3차원 지오메트리(Geometry) 정보 없이 주어진 이미지 사이의 관계를 바탕으로 가상 시점의 뷰를 합성하는 Image-based Rendering[3,4]이 대표적으로 사용되어 왔다. 최근에는 Neural Radiance Field (NeRF)[4]라는 새로운 접근 방법이 높은 관심을 받고 있다. NeRF는 Multi-Layer Perceptron (MLP) 네트워크 구조를 바탕으로 Light ray가 통과하는 3차원 공간상의 위치 정보(x, y, z)와 통과하는 방향(θ, φ)을 입력으로 받아, 대응되는 위치의 밀도(σ)와 RGB 값을 예측한다. 예측 정확도는 MLP 네트워크의 학습이 진행됨에 따라 높아지며, 일정 수준에서 saturation 된다. 학습을 마친 NeRF를 바탕으로, 임의의 자유 시점에 대한 뷰는 해당 뷰를 구성하는 데 필요한 Light ray를 정의하고, 이들을 NeRF를 통해 예측, 하나의 뷰의 형태로 구성함으로써 완성된다. NeRF를 통해 합성되는 뷰는 실제 이미지에 가까우면서도 동시에 정확도가 높다는 장점이 있다.
이러한 NeRF 기반 접근은 Light field (LF)[5,6,7]에도 적용되어, Neural LF (NeLF)[8,9,10]의 새로운 접근 방법이 제시되었다. LF는 자유 공간을 통과하는 다양한 light ray를 정의하고, 이들의 재조합을 통해 다양한 시점의 뷰를 합성하는 기술이다. 가장 대표적으로 사용되는 4차원의 LF는 두 개의 평면을 가정하고, 하나의 light ray가 통과하는 두 평면상의 두 점 (u, v)와 (s, t)를 통해 해당 light ray를 정의한다. 실제 구현에서 LF가 가정하는 light ray는 실제로 촬영된 이미지들의 픽셀로 대체되며, 매우 조밀한 LF를 구성하기 위해서는 조밀하게 촬영된 많은 수의 이미지가 필요하다. 현실적인 문제로 조밀한 LF 구성은 제한적이며, sparse한 LF로부터 조밀한 LF를 재구성하는 angular super-resolution[11,12]이 대체로 연구되었다. NeLF는 유사한 문제를 풀기 위한 방법으로 NeRF와 동일한 MLP 네트워크를 이용한다. 단, 입출력에 차이가 있는데, NeLF는 4차원 LF의 light ray를 정의하는 representation (u, v, s, t)을 입력으로, 해당 light ray의 색상 정보, RGB를 출력값으로 예측한다. NeRF와 달리 밀도는 예측하지 않는다. 또한 NeRF가 3차원 공간상의 밀도 값을 바탕으로 light ray의 최종 RGB 값을 예측하는 ray marching 과정을 포함하는 것과 달리, NeLF는 단순히 (u, v, s, t)의 representation을 RGB에 직접적으로 매칭하기 때문에 렌더링 속도가 빠르다. 반면, NeLF는 3차원 공간의 볼륨을 예측하지 못하는 한계가 있다.
NeRF와 NeLF는 새로운 접근 방법으로 3차원 이미지 처리의 다양한 분야로의 높은 확장성을 보여주고 있다. 하지만 이 두 기술은 대상 공간과 물체에 따라 학습성능에 큰 차이를 보인다. 대체로 대상 공간과 물체가 얼마나 복잡한지를 바탕으로 덜 복잡한 경우 높은 성능의 Peak Signal-to-noise ratio (PSNR) 수치를 보이는 반면, 복잡한 공간의 경우 PSNR 수치는 20dB 이하로 크게 떨어진다. 그림 1과 그림 2는 서로 다른 두 대상 공간을 동일한 크기의 NeLF로 학습한 결과를 보여준다. 학습에 사용되는 이미지의 프레임 수, 해상도 등 다른 조건은 동일하다. 그림 1의 나뭇잎과 같은 복잡한 형태의 샘플의 경우 17dB의 낮은 성능을 보이는 데 반해, 그림 2와 같이 비교적 간단한 형태의 샘플의 경우 28dB의 높은 성능을 보였다.
대체로 대상 공간과 물체가 복잡한 경우 성능이 떨어지는 경향은 알 수 있으나, NeRF와 NeLF의 합성 성능을 확인하기 위한 유일한 방법은 실제로 학습이 진행되어야 한다. NeRF와 NeLF는 차세대 3차원 미디어로 활용될 것으로 기대한다. 하지만 현재는 사용자가 원하는 수준의 PSNR을 목표로 NeRF와 NeLF를 학습하는 기술은 제한적이다. 현재 가장 많이 활용되고 있는 비디오의 경우 quantization parameter (QP)라는 옵션을 통해 사용자가 원하는 수준을 설정한다. NeRF와 NeLF 역시 추후 미디어로써 역할을 하기 위해서는 목표 PSNR을 고려한 학습 및 뷰 재구성 방법이 반드시 마련되어야 한다. 본 논문은 이를 위한 초기 연구로 NeLF를 대상으로 주어진 공간의 복잡도와 실제 학습된 성능 사이의 관계 분석을 연구 목표로 한다. 이때, 복잡도를 어떻게 정의할 것인가에 대한 고민이 필요하다. NeLF의 경우 다수 이미지를 바탕으로 공간을 학습하기 때문에 이미지의 복잡도를 고려할 수 있다. 이미지 복잡도를 객관적으로 평가하는 다양한 연구가 시도됐다. 초기 연구인 [13]은 온도(T)와 조화(H) 두 지표를 이용하여 이미지의 생명(L)과 복잡성(C)을 계산하여 이미지 복잡도를 정량적으로 나타낸다. [14]는 이미지의 서로 다른 영역 각각의 히스토그램 분포 간의 상호 정보를 계산하여 이미지 복잡도를 평가한다. [15]는 독립 성분 분석(ICA)을 사용하여 이미지 복잡성을 모델링한다. [16]은 색상 엔트로피 및 색상 프랙탈 차원의 관점으로 이미지 복잡도를 분석하였다. 최근의 연구에서는 많은 관찰자의 시각적 평가를 기반으로 이미지 복잡도를 정의했다[17].
앞서 언급한 바와 같이, 본 논문은 NeLF 학습을 위해 주어진 이미지에서 복잡도를 관측하고, 실제 학습성능과의 관계를 연구한다. 이를 위해, 이미지 복잡도를 나타낼 수 있는 여러 지표를 선별하고, 그 지표들이 NeLF 기술을 통한 이미지 합성 품질에 미치는 영향을 실험적으로 분석한다. 이미지의 압축된 파일 크기(Compressed image size), 색상 복잡도(Color Complexity), 에지의 비율(Edge Ratio), 라플라시안 분산(Variance of Laplacian, VOL), 특징점의 비율(Features), 그리고 비디오의 크기(Video Volume)의 여섯 가지 주요 지표를 중심으로 실험한다. 각 복잡도 평가지표에 대한 분석 이후에는 테스트를 위한 별도의 샘플들을 대상으로 예측된 PSNR과 실제 PNSR을 비교 검증하며, 결과를 분석한다.
Ⅱ. 이미지 복잡도 평가지표 및 예측 모델
1. 이미지 복잡도 평가지표
NeLF를 학습하기 위해 사용되는 데이터는 대상 공간 또는 물체를 촬영한 다수의 이미지이다. 다수의 이미지로부터 대상 공간 및 물체의 복잡도를 판단하기 위해 고려한 지표를 소개하고, 각 지표의 평가 방법을 소개한다.
일반적으로 이미지는 압축된 파일의 형태로 저장되는데, 대상 이미지의 압축 효율에 따라 압축된 파일 크기에 영향을 준다. 이미지 또는 한 프레임 내에서의 압축의 경우 대체로 주변 픽셀을 이용하여 대상 픽셀을 압축하며, 주변 픽셀로부터 예측(prediction) 난이도에 따라 압축 효율이 달라진다[18,19]. 일반적으로 복잡한 이미지는 공간적 픽셀 사이의 차이가 크고 예측이 어려우며, 압축 효율이 낮다. 반면, 색의 변화가 거의 없는 흰 벽과 같은 이미지는 예측이 쉽고, 압축 효율이 높다. 즉, 압축된 이미지 파일 크기는 해당 이미지의 복잡도를 간접적으로 나타내며, 본 연구는 이를 하나의 복잡도 평가지표로 사용한다.
본 연구에서는 OpenvCV에서 제공하는 imwrite 함수를 사용하여 JPEG 압축 표준으로 압축된 이미지의 파일 크기를 사용한다. imwrite 함수의 JPEG 압축 화질은 실험적으로 선택된 30을 사용한다.
이미지는 픽셀로 구성이 되며, 픽셀은 RGB 색으로 표현된다. 색은 이미지를 구성하는 기본적인 요소로써 이미지의 복잡도를 평가하는 데 매우 중요한 요소이다. 색상 복잡도에 관한 연구[20]는 색상 복잡도를 두 가지 측면에서 정의하는데 하나는 색상의 다양성이고, 다른 하나는 공간적인 분포이다. 공간적 분포는 유사한 색상이 인접한 픽셀에 얼마나 많이 위치하는지를 의미하며 이는 앞선 이미지 파일 크기 항목에서 압축 효율성과 유사한 관계를 가진다. 따라서 본 연구에서는 첫 번째 정의인 색상의 다양성을 기준으로 색상 복잡도를 정의하고 활용한다. 본 연구에서 사용한 색상 복잡도는 [20]의 수식을 그대로 활용하며 이는 (1)과 같다.
| (1) |
수식 (1)에서 m은 해당 이미지가 포함하는 색상의 전체 개수를 의미하고, ni는 i 번째 색상의 개수를 의미하며, N은 이미지가 포함하는 전체 픽셀 개수를 의미한다.
이미지 관점에서 에지는 색상이 급격하게 바뀌는 지점을 의미한다. 이는 픽셀값 예측 관점에서도 불리하게 작용하여, 압축 효율을 낮추거나, 이미지 합성 성능을 떨어뜨리는 요소로 작용한다. 이러한 측면에서 에지는 이미지 복잡도를 결정하는 하나의 요소로 활용될 수 있다[21,22]. 본 연구 역시 이미지 복잡도의 평가 요소로 에지를 고려한다. 수식 (2)는 이미지의 에지 비율 측정 수식을 나타낸다.
| (2) |
수식 (2)에서 Width, Height는 각각 이미지 길이, 높이를 의미하며, i는 이미지에 포함되어 있는 에지 픽셀의 인덱스를 의미한다. 본 연구에서는 에지 추출을 위해 Canny 알고리즘[23]을 사용하였으며, 에지는 그레이스케일에서 추정한다.
일반적으로 이미지에서 라플라시안(Laplacian) 연산은 해당 이미지의 흐릿함(Blur)를 평가하는데 사용된다. 라플라시안 연산 결과 수치가 낮은 경우 해당 이미지는 상대적으로 흐릿하다고 평가되며, 수치가 높은 경우 선명하다고 평가된다. 이는 에지 관점에서 에지가 얼마나 선명한지를 의미하기도 한다. 본 논문은 복잡도 평가 지표로써 라플라시안 분산(Variance of Laplacian)을 포함한다. 라플라시안 분산은 [24]에서 소개하고 있는 연산을 따르며 이는 (3)과 같다.
| (3) |
수식 (3)은 이미지의 라플라시안 분산을 계산하며, k와 l은 이미지 행렬의 행(row)과 열(column) 인덱스를 나타낸다. 라플라시안 연산은 각 픽셀 주변의 화소값 차이를 이용해 계산되어, 이미지의 에지 선명도를 평가하는 데 사용된다. 이때 μ는 라플라시안 값의 평균이고, σ2는 이 값들의 분산을 의미한다. 분산 값이 크면 이미지의 에지가 선명하다는 것을 나타내며, 이는 전반적인 이미지 품질의 지표로 활용된다.
특징점은 주어진 이미지에서 특별하게 취급될 수 있는 픽셀 포인트를 의미하며, 이는 서로 다른 이미지에서 동일한 픽셀 포인트를 탐지하는 매칭 방법에서 주로 활용된다. 특징점 추출 알고리즘에 따라 특징점으로 간주하는 픽셀에 차이가 있으나, 주로 특징점은 단조롭지 않은 점들이 선택된다. 대표적으로 Harris 알고리즘은 코너(Corner)를 특징점으로 간주하며[25], SIFT (Scale-Invariant Feature Trans- form)는 이미지 피라미드를 통해 크기에 덜 민감한 특징점을 고려한다[26]. 주어진 이미지에서 특징점이 많이 선택됨은 해당 이미지가 단조롭지 않음을 의미하며, 이를 고려하여 본 연구에서는 특징점의 비율을 또 하나의 평가지표로 활용한다. 식 (4)는 이미지의 특징점 비율 계산 수식을 보여준다.
| (4) |
Width, Height는 이미지 길이, 높이를 의미하며, i는 이미지에 포함된 특징점 픽셀의 인덱스를 의미한다. 본 연구에서는 특징점은 ORB (Oriented FAST and Rotated BRIEF) 알고리즘[26]을 사용하여 계산하며, 특징점은 그레이스케일에서 추출한다.
앞서 정의한 지표들은 단일 이미지 관점에서의 복잡도를 평가한다. 하지만 NeLF는 3차원 공간 또는 물체를 재구성하기 위해 서로 다른 이미지 사이의 관계를 고려한다. 대상 공간이 복잡한 경우 조금의 시점 변화에도 이미지가 크게 달라지는 결과를 초래하고, 반대로 단순한 공간에서는 시점이 변하더라도 이미지가 크게 다르지 않다. 즉, NeLF 학습을 위해 주어진 이미지들이 얼마나 유사한지에 따라 NeLF 학습의 난이도에 영향을 준다.
본 연구는 이미지들 사이의 유사도를 평가하기 위해 압축된 비디오 파일의 크기를 복잡도 평가지표로 포함한다. H.264[27], HEVC[19]와 같은 비디오 코덱은 시간적으로 인접한 프레임 픽셀을 활용하여 대상 프레임의 픽셀을 예측하고, 압축한다. 인접한 프레임 사이의 유사도가 높은 경우 압축 효율이 높으며, 압축된 비디오 파일 크기는 작아지는 반면, 유사도가 낮은 경우 압축 효율이 낮아 파일 크기가 커지게 된다. 따라서 압축된 비디오 파일 크기는 간접적으로 이미지들 사이의 유사도를 보여준다.
본 연구는 OpenCV VideoWirte 클래스를 사용하여 주어진 이미지들을 시간 축으로 연결, MPEG-4 코덱으로 압축하여 만들어진 비디오 파일의 크기 값을 사용한다.
2. 예측 모델
본 연구는 이미지 복잡도 지표와 NeLF의 학습성능 관계를 분석하기 위해 선형회귀 모델을 이용한다. 여러 복잡도 범위의 학습성능을 분석하기 위해 다양한 이미지 샘플에 대한 학습을 수행했다. 이 과정에서 해상도와 프레임 수 등을 통제하여 NeLF의 학습성능에 이미지 복잡도 지표만 영향을 미치도록 했다. 각 복잡도 지표의 데이터를 사용하여 PSNR을 종속 변수로 하는 선형회귀를 수행하고 지표별로 기울기와 절편을 계산했다.
분석 결과는 각 복잡도 지표에 따른 PSNR의 분포와 회귀선을 보여주는 산점도로 시각화되었다. 이 시각화는 각 지표가 PSNR과 어떻게 관련되는지를 직관적으로 이해할 수 있게 돕고, 데이터 포인트들이 회귀선을 중심으로 어떻게 분포하는지를 보여주어 각 지표와 학습성능과의 상관도 평가한다. 각 지표의 성능은 결정계수 R-squared 값을 계산하여 평가되었으며, 이 값은 각 지표가 PSNR의 변동을 얼마나 잘 설명하는지를 나타낸다. 특히, R-squared 수치가 높은 지표는 학습성능 예측에 있어 유용성이 높다고 평가되며, 해당 지표의 회귀선 바탕으로 NeLF 학습의 성능을 예측할 수 있는 NeLF 학습성능 예측 모델을 구성한다.
Ⅲ. 실험 결과
1. 실험 환경
앞서 소개한 복잡도 평가지표들을 바탕으로 다양한 샘플에서의 복잡도를 평가하고, 실제 NeLF를 이용한 학습 결과와의 관계를 분석한다. 본격적인 실험에 앞서 실험 환경을 소개한다.
본 논문은 [8]에서 제시한 NeLF 모델을 기반으로 실험을 수행한다. 해당 MLP 네트워크는 4차원의 light rays 표현과 해당 light rays의 RGB 값을 매칭하도록 학습한다. 그리고 변인통제를 위해 표 1과 같이 몇 가지 변수를 고정하여 실험을 진행한다. 모든 샘플 데이터의 해상도를 960 × 540로 고정하며, NeLF 학습에 사용되는 이미지 개수는 40장으로 고정한다. MLP 네트워크 크기는 depth와 width를 각각 8, 256으로 고정한다. 여기서 depth는 MLP의 input, output layer를 제외한 hidden layer의 개수를 의미하며, width는 hidden layer의 길이를 의미한다. NeLF 학습은 200 epoch으로 고정한다.
실험에서 사용한 샘플은 NeRF, NeLF 연구에서 주로 사용하는 nerf_llff 데이터 샘플을 기본적으로 사용하며, nerf_llff 데이터 샘플의 개수는 8개로 추세를 분석하기에 제한적인 점을 고려하여, 22개의 샘플을 직접 촬영하여 포함하였다. 그림 3과 그림 4는 실험에서 사용된 nerf_llff 샘플과 직접 촬영한 샘플의 일부를 보여준다.
2. 복잡도 평가 결과와 NeLF 성능의 관계 분석
그림 5는 주어진 30개의 샘플을 대상으로 NeLF로 학습한 PSNR 성능과 각 복잡도 평가지표 사이의 관계 그래프를 보여준다. 그림 5 (a), (b), (c), (d), (e), (f)는 각각 압축된 이미지 파일 크기, 압축된 비디오 파일 크기, 색상 복잡도, 에지 비율, 라플라시안 분산, 특징점 비율에 대한 그래프를 나타낸다. 각 그래프에서 가로축은 각 평가지표의 수치를 의미한다. 수치가 클수록 각 평가지표 기준으로 복잡도가 높아짐을 의미한다. 그래프의 세로축은 NeLF 학습성능 PSNR을 나타낸다. 값이 클수록 원본에 가까운 이미지가 만들어짐을 의미하며, 이는 성능이 우수함을 의미한다.
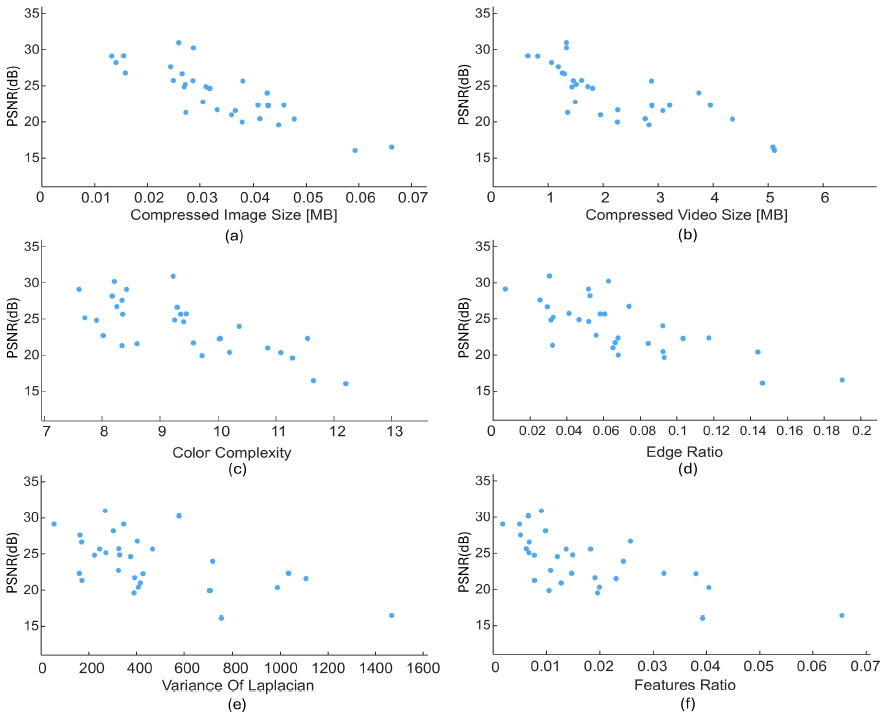
Image Complexity Measurement and NeLF Learning Performance(PSNR) Graph (a) Compressed Image Size (b) Compressed Video Size (c) Color Complexity (d) Edge Ratio (e) Variance Of Laplacian (f) Features Ratio
6개의 그래프에서 전반적으로 점들이 우하향하는 경향을 보인다. 이는 복잡도가 높을수록 NeLF 학습성능이 떨어짐을 의미한다. 이는 본 연구에서 초기 가정한 바와 같이 대상 공간 및 물체의 복잡도가 높을수록 NeLF 학습에 불리한 영향을 끼치며, 그 결과 성능이 떨어짐을 의미한다.
그림 6은 garlic, items, orchids 샘플의 원본 이미지와 NeLF 합성 이미지를 비교한다. 해당 샘플의 학습성능과 평가지표는 표 2와 같다. 세 샘플의 학습성능은 순서대로 28.19dB, 21.57dB, 16.05dB이며, 대체로 평가지표와 음의 상관관계를 나타냄을 확인할 수 있다. 라플라시안 분산의 경우 items 샘플이 orchids 샘플보다 높은 데 반해, orchids 샘플의 PSNR이 더 높은 것으로 나타난다.

Comparison of Original Image) and Reconstructed Image (a) garlic(original) (b) garlic(reconstructed) (c) items(original) (d) items(reconstructed) (e) orchids(original) (f) orchids(reconstructed)
3. 복잡도 평가지표와 NeLF 성능의 상관성 비교
그림 7은 그림 5의 각각의 이미지 복잡도 지표에 대해 선형회귀를 수행한 결과를 보여준다. 이 그림들은 각 지표가 PSNR과 어떻게 관련되는지를 직관적으로 이해할 수 있게 돕고, 데이터 포인트들이 회귀선을 중심으로 어떻게 분포하는지를 보여줌으로써 각 지표의 예측 효과를 시각적으로 평가할 수 있다.
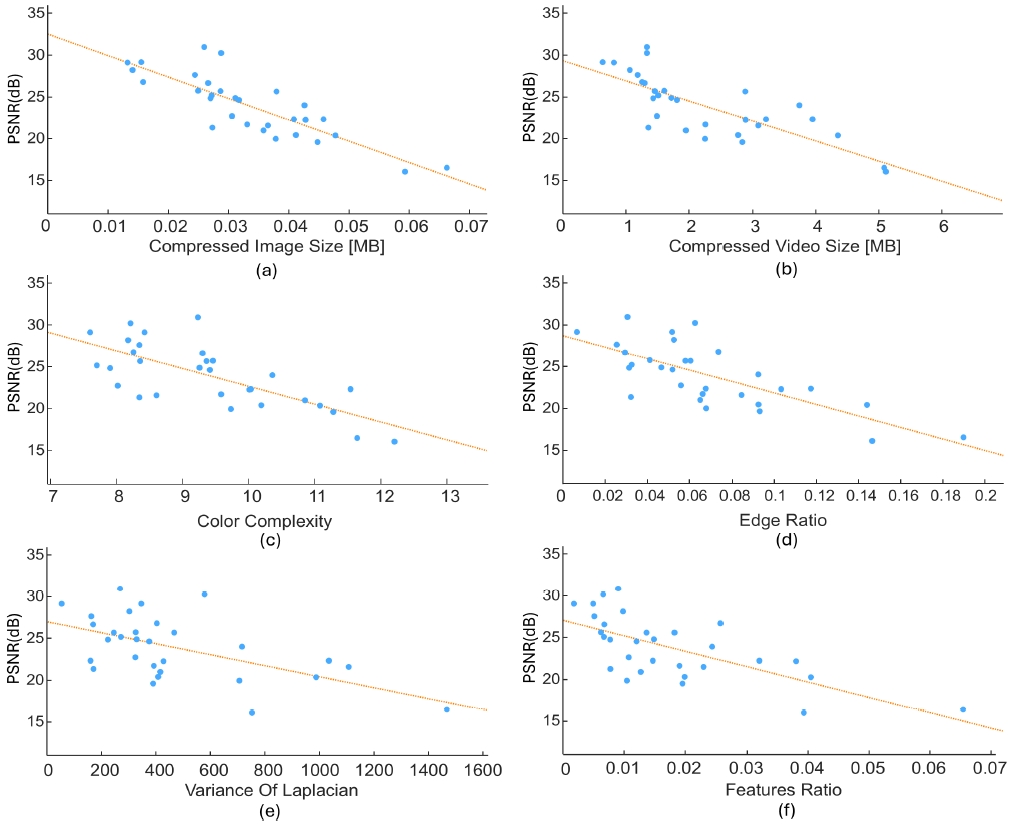
Image Complexity Measurement and NeLF Learning Performance(PSNR) Graph with Linear Regression Results (a) Compressed Image Size (b) Compressed Video Size (c) Color Complexity (d) Edge Ratio (e) Variance Of Laplacian (f) Features Ratio
표 3은 그림 7에서 제시된 각 지표에 대한 선형 회귀 분석 결과의 결정계수 R-squared 값을 나타낸다. 표 3에서 R-squared 수치가 클수록 해당 이미지 복잡도 지표와 NeLF 학습성능 PSNR과의 상관도가 높다고 평가할 수 있다. 표 3은 다양한 NeLF 크기에서의 경향성과 일관성을 확인하기 위해 NeLF의 depth와 width를 다양하게 바꿔가며 상관도을 비교한다. 그림 7의 경우 depth와 width가 각각 8, 256인 NeLF에 대한 결과이다. 상관도가 가장 높은 수치를 빨간색, 두 번째로 높은 수치를 녹색으로 표시하였다. 표 3의 결과를 보면 일관적으로 압축된 이미지 파일 크기의 상관도가 가장 높았으며, 압축된 비디오 파일 크기의 상관도가 두 번째로 높은 것을 확인할 수 있었다. 반면, 그림 6과 표 2의 비교에서 경향이 달랐던 라플라시안 분산의 경우 상대적으로 가장 낮은 R-sqaured 값을 보인 것을 확인할 수 있으며, 다른 지표들에 비해 NeLF 학습성능과의 관련성이 다소 낮음을 의미한다.
추가적으로 표 3의 결과를 보면 depth와 width가 증가함에 따라 R-squared 값이 감소하는 상관도가 저하하는 경향을 보인다. 대체로 MLP 크기가 커짐에 따라 학습 능력이 향상되고, PSNR이 증가하는데, 샘플에 따라 PSNR 증가 정도가 달라, PSNR의 편차가 커지는 결과를 확인하였으며, 이에 따른 상관도 저하로 판단된다.
4. 복잡도 평가지표를 이용한 NeLF 성능 추정 실험 결과
마지막으로 앞선 선형회귀 모델을 바탕으로 임의의 주어진 샘플에 대하여 최종 합성 성능을 예측하고, 이를 실제 학습 값과 비교한다. 총 네 가지의 예측 모델을 비교한다. 하나는 표 3의 결과에서 상관도가 가장 높은 압축된 이미지 파일 크기를 기반으로 하는 선형회귀 모델이고, 두 번째 모델은 두 번째로 상관도가 높은 압축된 비디오 파일 크기를 기반으로 하는 선형회귀 모델이다. 세 번째 모델은 압축된 이미지 파일 크기와 압축된 비디오 파일 크기 두 개를 동시에 이용한 선형회귀 모델이며, 마지막 모델은 6개 지표를 모두 활용하는 다중선형회귀 모델이다.
그림 8은 예측 실험에 사용된 다섯 개의 테스트 이미지 샘플 (a) nutrients, (b) forklift, (c) hedges, (d) vanes, (e) playground를 보여준다. 그리고 표 4는 네 개 예측 모델에 대하여, 각 테스트 이미지 샘플에 대해 예측된 PSNR와 실제 NeLF를 통해 학습된 PSNR, 그리고 오차를 보여준다. 빨간색으로 표시된 수치는 단일 샘플에서 예측 모델별로 가장 작은 오차를 의미한다. 예측 모델별로 비교하면, 평균적으로 6개의 평가지표를 모두 고려하는 예측 모델의 오차가 가장 작은 것을 확인할 수 있다. 샘플별로는 항상 6개의 평가지표를 고려하는 것이 우수하지는 않았으며, vanes 샘플에서는 압축된 이미지 크기와 압축된 비디오 크기, playground 샘플에서는 압축된 비디오 크기 지표에서 오차가 가장 작았다. 샘플별로 평균 오차를 보면 최대 5.33dB에서 최소 0.07dB의 오차로 샘플에 따라 예측 오차가 큰 경우를 확인할 수 있다. 6개의 평가 지표는 각각의 특성에 따라 PSNR과의 서로 다른 경향을 가지며, 이를 복합적으로 사용하는 6개의 지표를 사용한 다중선형회귀 모델의 성능이 가장 우수한 결과를 보인다.
본 연구에서는 선형회귀라는 가장 단순한 예측 모델이 사용되었고, 이에 따라 예측 모델이 샘플에 따라 정확도에 다소 차이가 있는 것으로 판단된다.
Ⅳ. 결론 및 향후 계획
NeLF는 다수 이미지를 바탕으로 대상 공간 또는 물체를 재구성하는 접근 방법으로, 대체로 대상 공간의 복잡도에 따라 학습성능이 달라진다. 복잡도가 높은 물체를 포함하거나 Lambertian 특성을 포함하여 이미지 전반의 복잡도가 높은 샘플의 경우 학습성능이 떨어지는 반면, 공간이 단조로울 경우 높은 PSNR로 학습된다. 단, 실제 수치를 알기 위해서는 학습이 불가피한데, 본 논문은 이를 실제로 학습하지 않고 NeLF 학습에 사용되는 입력 이미지들을 바탕으로 예측하는 것을 주요 연구 목표로 한다. 이를 위해 NeLF 학습성능과 관련성이 높은 이미지 복잡도를 탐색한다. 본 논문은 압축된 이미지 파일 크기, 색상 복잡도, 에지 비율, 라플라시안 분산, 압축된 비디오 파일 크기, 특징점 비율의 6개 지표를 고려하며, NeLF 학습성능과의 선형회귀를 통해 상관도를 비교한다. 실험 결과 앞선 6개 지표 중에서는 압축된 이미지 파일 크기, 압축된 비디오 파일 크기의 복잡도 지표가 상대적으로 상관도가 높았다. 테스트용 샘플을 대상으로 하는 예측 실험에서는 샘플에 따른 편차가 있었으나 평균적으로 6개의 지표가 모두 활용된 선형회귀 모델에서 오차가 가장 작았다.
본 연구는 대체로 사용되는 평가지표를 바탕으로 선형회귀라는 가장 단순한 예측 모델이 사용되었다는 점에서 샘플에 따라 오차 수준이 큰 이슈가 있었으며, 향후 이를 보완하기 위해 물체 단위로 복잡도를 판단하거나 Lambertian 특성을 고려하는 등의 세부적인 평가지표를 개발하고, 보다 복잡한 예측 모델을 통해 예측성능을 높이는 것을 연구 목표로 한다.
Acknowledgments
This work was supported by Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government(MSIT) (No.RS-2023-00229330, 3D Digital Media Streaming Service Technology)
Follwing are results of a study on the "Leaders in Industry-university Cooperation 3.0" Project, supported by the Ministry of Education and National Research Foundation of Korea.
References
-
K. Chen, Y. K. Lai, & S. M. Hu, “3D indoor scene modeling from RGB-D data: a survey,“ Computational Visual Media, Vol. 1, pp.267-278, 2015.
[https://doi.org/10.1007/s41095-015-0029-x]

-
B. Mildenhall, P.P. Srinivasan, R. Ortiz-Cayon, N.K. Kalantari, R. Ramamoorthi, R. Ng, A. Kar, “Local light field fusion: Practical view synthesis with prescriptive sampling guidelines,” ACM Trans Graph, Vol. 38, No. 4, pp.1-14, 2019.
[https://doi.org/10.1145/3306346.3322980]

-
S. C. Chan, H. Y. Shum, & K. T. Ng, “Image-based rendering and synthesis,” IEEE Signal Processing Magazine, Vol. 24, No. 6, pp.22-33, 2007.
[https://doi.org/10.1109/MSP.2007.905702]

-
B. Mildenhall, P. P. Srinivasan, M. Tancik, J. T. Barron, R. Ramamoorthi, & R. Ng, “Nerf: Representing scenes as neural radiance fields for view synthesis.” Communications of the ACM, Vol. 65, No.1, pp.99-106, 2021.
[https://doi.org/10.1145/3503250]

-
E. H. Adelson, & J. R. Bergen, “The plenoptic function and the elements of early vision,” in Computation Models of Visual Processing, M. S. Landy and J. A. Movshon, Eds., Cambridge, MA, USA: MIT Press, pp.3-20, 1991.
[https://doi.org/10.7551/mitpress/2002.003.0004]

-
M. Levoy, & P. Hanrahan, “Light field rendering,” in Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques., pp.31-42, 1996.
[https://doi.org/10.1145/237170.237199]

-
S. J. Gortler, R. Grzeszczuk, R. Szeliski, and M. F. Cohen, “The lumigraph,” in Proceedings 23rd Annual Conference on Computer Graphics and Interactive Techniques., pp43-54, 1996.
[https://doi.org/10.1145/237170.237200]

-
Z. Li, L. Song, C. Liu, & J. Yuan, “Neulf: Efficient novel view synthesis with neural 4d light field,” arXiv preprint arXiv:2105.07112, , pp.1-11, 2021.
[https://doi.org/10.48550/arXiv.2105.07112]

-
B. Attal, J.-B. Huang, M. Zollhöfer, J. Kopf, and C. Kim, “Learning neural light fields with ray-space embedding networks,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, pp.19819-19829, 2022.
[https://doi.org/10.1109/CVPR52688.2022.01920]

-
M. Suhail, C. Esteves, L. Sigal, and A. Makadia, “Light field neural rendering,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, pp.8269-8279, 2022.
[https://doi.org/10.1109/CVPR52688.2022.00809]

-
J. Jin, J. Hou, H. Yuan, & S. Kwong, “Learning light field angular super-resolution via a geometry-aware network,” In Proceedings of the AAAI conference on artificial intelligence, Vol. 34, No. 07, pp.11141-11148, April, 2020.
[https://doi.org/10.1609/aaai.v34i07.6771]

-
S. Wanner and B. Goldluecke, “Spatial and angular variational super-resolution of 4D light fields,” in Proceedings of the 12th European Conference on Computer Vision (ECCV), Florence, Italy, pp.608-621, 2012.
[https://doi.org/10.1007/978-3-642-33715-4_44]

- A. Klinger and N. A. Salingaros, “Complexity and visual images,” Technical Report, University of California, 1998, http://www.cs.ucla.edu/~klinger/image_complexity_7_1_97.html.bak, (accessed July 15, 2024).
-
J. Rigau, M. Feixas, and M. Sbert, “An information-theoretic framework for image complexity,” in Computational Aesthetics in Graphics, Visualization, and Imaging, Girona, Spain, pp.177-184, 2005.
[https://doi.org/10.2312/compaesth/compaesth05/177-184]

-
J. Perkiö and A. Hyvärinen, “Modelling image complexity by independent component analysis, with application to content-based image retrieval,” in Artificial Neural Networks – ICANN 2009: 19th International Conference, Limassol, Cyprus, pp.704-714, 2009.
[https://doi.org/10.1007/978-3-642-04277-5_71]

-
M. Ivanovici, R. M. Coliban, C. Hatfaludi, and I. E. Nicolae, “Color image complexity versus over-segmentation: A preliminary study on the correlation between complexity measures and number of segments,” Journal of Imaging, Vol. 6, No. 4, pp.16, 2020.
[https://doi.org/10.3390/jimaging6040016]

-
S. Athar and Z. Wang, “A comprehensive performance evaluation of image quality assessment algorithms,” IEEE Access, Vol. 7, pp.140030-140070, 2019.
[https://doi.org/10.1109/ACCESS.2019.2943319]

-
M. W. Marcellin, M. J. Gormish, A. Bilgin, and M. P. Boliek, “An overview of JPEG-2000,” in Proceedings DCC 2000. Data Compression Conference, Snowbird, UT, USA, Mar. pp.523-541, 2000.
[https://doi.org/10.1109/DCC.2000.838192]

-
G. J. Sullivan, J. R. Ohm, W. J. Han, and T. Wiegand, “Overview of the high efficiency video coding (HEVC) standard,” IEEE Transactions on Circuits and Systems for Video Technology, Vol. 22, No. 12, pp.1649-1668, 2012.
[https://doi.org/10.1109/TCSVT.2012.2221191]

-
B. Zhou, S. Xu, and X. X. Yang, “Computing the color complexity of images,” in Proceedings of the 2015 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Zhangjiajie, China, pp.1898-1902, Aug, 2015.
[https://doi.org/10.1109/FSKD.2015.7382237]

-
H. Yu and S. Winkler, “Image complexity and spatial information,” in Proceedings of the 2013 Fifth International Workshop on Quality of Multimedia Experience (QoMEX), Klagenfurt, Austria, pp.12-17, July, 2013.
[https://doi.org/10.1109/QoMEX.2013.6603194]

-
V. Maksimovic, M. Petrovic, D. Savic, B. Jaksic, and P. Spalevic, “New approach of estimating edge detection threshold and application of adaptive detector depending on image complexity,” Optik, Vol. 238, pp.166476, 2021.
[https://doi.org/10.1016/j.ijleo.2021.166476]

-
J. Canny, “A computational approach to edge detection,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. PAMI-8, pp.679-698, 1986.
[https://doi.org/10.1109/TPAMI.1986.4767851]

-
M. Amin-Naji and A. Aghagolzadeh, “Multi-focus image fusion using VOL and EOL in DCT domain,” arXiv preprint arXiv:1710.06511, , pp.728-733, 2017.
[https://doi.org/10.48550/arXiv.1710.06511]

- J. Chen, L. H. Zou, J. Zhang, and L. H. Dou, “The comparison and application of corner detection algorithms,” Journal of Multimedia, Vol. 4, No. 6, pp.435-443, 2009.
-
E. Karami, S. Prasad, and M. Shehata, “Image matching using SIFT, SURF, BRIEF and ORB: performance comparison for distorted images,” arXiv preprint arXiv:1710.02726, , p.1-5, 2017.
[https://doi.org/10.48550/arXiv.1710.02726]

- N. Özbek and T. Tunali, “A survey on the H.264/AVC standard,” Turkish Journal of Electrical Engineering and Computer Sciences, Vol. 13, No. 3, pp.287-302, 2005.

- 2018년 3월 ~ 현재 : 서울과학기술대학교 전자IT미디어공학과 학사
- ORCID : https://orcid.org/0009-0002-8119-323X
- 주관심분야 : 실감미디어, 컴퓨터 비전

- 2014년 2월 : 경희대학교 전자전파공학과 학사
- 2016년 2월 : 서울대학교 전기정보공학부 석사
- 2020년 8월 : 서울대학교 전기정보공학부 박사
- 2023년 3월 ~ 현재 : 서울과학기술대학교 스마트ICT융합공학과 조교수
- ORCID : https://orcid.org/0000-0001-8216-5842
- 주관심분야 : 실감미디어(가상현실, 증강현실, 메타버스), 영상처리, 컴퓨터 비전






