
위상 홀로그램의 픽셀피치 변화에 따른 적정 전파거리에 대한 고찰
Copyright © 2024 Korean Institute of Broadcast and Media Engineers. All rights reserved.
“This is an Open-Access article distributed under the terms of the Creative Commons BY-NC-ND (http://creativecommons.org/licenses/by-nc-nd/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited and not altered.”
초록
컴퓨터 생성 홀로그래피 이미지를 생성하는 현재 방식은 일반 이미지와 달리, 각 디스플레이 장치의 환경에 맞게 최적화하는 방식이다. 같은 영상을 여러 장치에서 디스플레이하기 위해 각기 다른 장치마다 별도의 홀로그램 이미지를 제작해야만 하는 것이다. 이 과정은 컴퓨팅 자원의 낭비를 불가피하게 만든다. 따라서 같은 영상을 다양한 디스플레이 장치에 효과적으로 적용할 수 있는 방법이 필요하다. 본 논문은 하나의 홀로그램 이미지를 서로 다른 픽셀피치의 디스플레이 장치에서 디스플레이할 때 적정 전파거리를 계산하는 방법을 제안하고 실험을 통해 그 효과를 증명한다. 또한, 프레넬 근사가 어려운 매우 가까운 전파거리에서도 이 계산 방식이 유효함을 실험적으로 보여준다.
Abstract
The current method of generating computer-generated holographic images, unlike regular images, requires optimization for each display device's environment. To display the same image across multiple devices, it is necessary to create separate holographic images for each device. This process inevitably leads to the wastage of computing resources. Therefore, a method is needed to effectively apply the same image across various display devices. This paper proposes a method to calculate the optimal propagation distance for displaying a single holographic image on display devices with different pixel pitches, and demonstrates its effectiveness through experiments. Additionally, it experimentally shows that this calculation method remains valid even at very close propagation distances where Fresnel approximation is challenging.
Keywords:
Hologram, Propagation Distance, Computer-Generated Hologram, Display EnvironmentⅠ. 서 론
홀로그램은 2차원 간섭무늬를 이용해서 3차원 정보를 복원하는 차세대 디스플레이 기술이다. 그중에서도 컴퓨터 생성 홀로그램(Computer Generated Hologram, CGH)은 컴퓨터를 이용해서 생성한 디지털 홀로그램을 지칭한다. 생성한 CGH를 공간 광 변조기(Spatial Light Modulator, SLM)를 통해 디스플레이 하면 홀로그램에 기록된 영상을 볼 수 있다. 현재까지는 디스플레이 기술의 한계로 진폭과 위상을 동시에 디스플레이 할 수 없다. 때문에, SLM은 진폭만을 디스플레이 하거나 위상만을 디스플레이 해야 한다. 두 방식 중에서 위상을 디스플레이 하는 방식은 다른 방식에 비해 참조광을 더 효율적으로 사용할 수 있다[1]. 때문에, 주로 사용하는 방식은 위상 홀로그램(Phase Only Hologram, POH)이다. 위상 홀로그램을 생성하는 방법에는 이중 위상 표현을 활용하는 Double Phase Amplitude Coding (DPAC)[2], 반복 최적화 기법을 활용하는 GS-Algorithm[3], SGD, 인공 신경망을 사용하는 HoloNet[4] 등이 있다. 위의 방법들은 모두 홀로그램 생성 과정에서 특정한 SLM 디스플레이 환경(픽셀피치, 파장, 전파거리)을 단독으로 고려한다.
다른 미디어 콘텐츠의 디스플레이 시나리오처럼, 홀로그램도 하나의 콘텐츠를 여러 디스플레이 장치를 이용해서 디스플레이 하는 one-source multi-use 시나리오를 고려해야 한다. 그런데 일반 이미지를 디스플레이 할 때와는 달리, 홀로그램 이미지의 경우에는 고려해야 할 사항이 더 많다. 일반 디지털 이미지의 경우에는 하나의 이미지를 서로 다른 여러 장치에서 디스플레이 하더라도 이미지를 보는 데에 아무런 문제가 없다. 하지만, 홀로그램 이미지의 경우에는 각각의 홀로그램이 각각의 SLM 환경에 최적화되어 생성되기 때문에 SLM 기기별로 전부 다른 홀로그램 이미지를 사용해야 한다. 이러한 방식은 생성된 홀로그램 콘텐츠의 활용 범위를 홀로그램 생성 시 가정한 SLM 환경으로 제약하기 때문에 홀로그램 서비스 확산의 장애 요소로 작용한다.
그림 1을 보면 같은 위상 홀로그램을 디스플레이 할 때, SLM 장치의 픽셀피치와 같은 물리적 환경 설정이 변하면 의도했던 전파거리에서 목표 이미지가 보이지 않는 것을 확인할 수 있다. 그림 1(c)는 픽셀피치가 달라진 SLM 환경에서 그림 1(a)의 위상 홀로그램을 생성될 당시의 전파거리에서 Band-Limited Angular Spectrum Method(BL-ASM) 방법[5]으로 수치적 복원했을 때의 이미지이다. 의도했던 목표 이미지가 아닌 잡음에 가까운 이미지가 보이는 것을 확인할 수 있다. 그런데, 다른 SLM 환경이더라도 전파거리를 조절하면 그림 1(d)와 같이 이미지가 잘 보이는 것을 확인할 수 있다. 이처럼 환경이 변하더라도 이미지가 잘 보이는 거리를 계산할 수 있다면, 위상 홀로그램 one-source multi-use 시나리오 연구에 도움이 될 수 있다.

(a) A phase only hologram optimized and created for a pixel pitch of 3.6μm and a propagation distance of 20cm (b) An image numerically reconstructed using the BL-ASM method when the POH in (a) is propagated in the optimized environment (c) An image numerically reconstructed using the BL-ASM method when the POH in (a) is propagated in an unoptimized environment with a pixel pitch of 7.2μm (d) An image numerically reconstructed using the BL-ASM method when the POH in (a) is propagated in an environment with a pixel pitch of 7.2μm and a propagation distance of 80cm
본 연구에서는 위상 홀로그램의 one-source multi-use 시나리오를 위한 기반 연구로서 특정한 픽셀피치의 SLM을 목표로 생성한 홀로그램을 다른 픽셀피치의 SLM에서도 올바르게 재현하기 위한 전파거리를 수학적으로 유도하고 실험적으로 검증하고자 한다. 논문의 Ⅱ장에서는 ASM 방법을 공간 영역의 합성곱 연산으로 해석하고, 적정 전파거리 유도에 사용될 변수들을 정의할 것이다. Ⅲ장에서는 Ⅱ장을 바탕으로 SLM의 픽셀피치가 변하면 적정 전파거리가 어떻게 변하는지를 계산할 것이다. Ⅳ장에서는 증명에 사용된 근사조건과 프레넬 근사조건과의 상관성을 따져볼 것이다. Ⅴ장에서는 앞서 계산된 결과가 성립하는지를 실험적으로 확인할 것이며, 근사조건이 성립하는 범위와 성립하지 않는 범위에서 결과가 어떻게 나타나는지를 비교할 것이다.
Ⅱ. 빛의 전파과정의 수학적 모형
본 장에서는 적정 전파거리를 유도하기 위해 빛의 전파를 계산하는 데에 사용되는 ASM 방식과 BL-ASM 방식[5]을 공간 영역의 합성곱 연산으로 해석하고 사용될 변수들을 정의할 것이다. 1절에서는 ASM 전파방식을 해석할 것이다. 2절에서는 BL-ASM 방식의 대역폭 제한이 ASM 전파방식의 수식을 어떻게 바꾸는지를 논하고, 수식을 정의할 것이다.
1. ASM 전파방식
ASM 전파방식은 광학에서 전자기파의 전파를 수치적으로 계산할 때 사용하는 방법이다. ASM 전파방식의 수식은 (1)과 같다[5].
| (1) |
| (2) |
| (3) |
| (4) |
(1), (2)의 g(x, y;0)는 전자기파의 전파가 시작되는 평면의 wavefield를 나타낸 함수로 (x, y) 좌표에 해당하는 복소진폭을 반환한다. 본 논문에서 g(x, y;0)은 SLM 평면의 (x, y) 좌표에서의 복소진폭을 나타내는 함수이다. ASM 전파방식에서 (1)에 대입하는 x와 y는 SLM 평면 위의 실제 물리적 위치이다. 그런데, 디지털 위상 홀로그램의 전파를 계산한다면, 좌표 (x, y)가 실제 물리적 위치가 아닌 상대적인 위치를 나타내는 값으로 생각하는 것이 편리하다. 예를 들어 인접한 두 광원 사이의 거리가 6.3μm인 SLM 장치에서 (x, y)에 해당하는 물리적 위치와 (x + 1, y)에 해당하는 물리적 위치 사이의 거리는 6.3μm이다. (1)의 HAS는 전파 함수를 의미한다. (3)은 HAS의 수식이다. g(x, y;d)는 SLM 평면과 평행하고, SLM 평면으로부터 d만큼 떨어진 wavefield의 복소진폭을 나타낸 함수이다.
만약 홀로그램이 전파거리 d에 최적화되어 형성되었다면, g(x, y;d)는 목표 이미지가 나타나는 목표 평면이라고 할 수 있다. F와 F - 1은 각각 푸리에 변환과 푸리에 역변환을 의미한다. 일반적으로 ASM 전파방식의 계산은 (1)처럼 푸리에 영역에서 계산한 뒤 역변환을 취해서 계산한다. 하지만, 직관적인 이해를 위해서는 (2)처럼 공간 신호 영역의 합성곱 연산으로 해석하는 것이 편리하다. 이때 전파 커널인 hAS는 전파 함수인 HAS를 푸리에 역변환하는 것으로 계산할 수 있다. (4)는 hAS의 수식이다[6]. 함수 hAS를 진폭과 위상이 구분되는 형태로 고치면 (5)가 성립한다.
| (5) |
| (6) |
(5)에서 변수 x와 y는 항상 x2 + y2 꼴로 쓰이는 것을 볼 수 있다. 이때 x2 + y2 를 w2으로 치환하면, 더 간단하고 직관적인 (6)을 얻을 수 있다. 여기서 w는 SLM 평면에서 커널의 중심으로부터 떨어진 거리를 의미한다.
위상 변조 SLM의 표면에 있는 화소들은 진폭의 크기가 모두 같고, 위상이 각각 다른 광원이다. 이때 SLM 표면의 좌표 (x, y)에서의 복소진폭은 (7)로 나타낼 수 있다.
| (7) |
(7)에서 복소진폭의 크기가 1인 이유는 계산의 편의를 위해서이다. 실제로 SLM 장치에 입력하는 디지털 위상 홀로그램 신호는 ϕ(x, y)라고 할 수 있다. 합성곱 연산의 정의에 따라 목표 평면의 wavefield인 g(x, y;d)는 (8)로 계산할 수 있다.
| (8) |
(8)에서 p는 픽셀피치를 의미한다. xs, ys를 사용하는 이유는 g(x, y;d)의 x, y와 구분하기 위해서이다. xs, ys는 ws의 상대적인 위치를 나타낸 값이고 hAS에는 실제 물리적 거리를 대입해야 하므로, 스케일 값으로 p를 곱해줘야 한다. 정리하면, 목표 평면의 (x, y)좌표에서의 복소진폭인 g(x, y;d)는 SLM 평면의 wavefield g(x, y;0)의 원소들에 각각의 위치에 대응하는 가중치인 h(pw;d)를 곱해서 더한 선형 결합으로 표현할 수 있다.
2. BL-ASM 전파방식
BL-ASM 방식은 ASM 방식을 디지털 도메인에서 적용할 때 발생하는 에일리어싱 현상을 막기 위해 [5]에서 고안된 방식이다. BL-ASM 방식은 ASM 전파방식의 전파 함수인 (1)의 HAS 대신 (9)의 HBLAS를 사용한다.
| (9) |
| (10) |
(9)에서 p, q는 연속 도메인의 u, v를 표본화한 것이다. rect는 범위를 제한하는 구형함수를 나타낸다. uBL, vBL은 에일리어싱이 발생하지 않는 주파수 영역의 최댓값이다. Δu,Δv는 주파수 영역의 표본 간격이다. (9)를 푸리에 역변환해서 (2)와 같은 꼴로 나타내면 수식 (11)과 같이 나타낼 수 있다.
| (11) |
| (12) |
(11)에서 sinc(•)의 수식은 (12)이다. 여기서 알 수 있는 사실은, BL-ASM 방식은 ASM 방식으로 계산한 g(x, y;d)에 sinc(•)를 이용한 저주파 필터를 씌우는 방식이라는 것이다.
Ⅲ. 픽셀피치 변화에 따른 적정 전파거리의 유도
이번 장에서는 Ⅱ장의 배경지식을 바탕으로 픽셀피치가 달라진 상황에서의 적정 전파거리를 찾아보도록 하겠다. 앞서 원본 위상 홀로그램의 wavefield를 g(x, y;d)라고 정의하고 이때의 적정 전파거리를 d라고 했다. 마찬가지로 해상도는 동일하고 픽셀피치만 sp로 바뀐 새로운 위상 홀로그램의 wavefield를 g'(x, y;d)이라고 하겠다. 그리고 이때의 적정 전파거리는 d'이라고 하겠다. 그림 2를 보면 d와 d'의 관계를 직관적으로 알 수 있다. 표 1에는 각 전파 상황의 변수들이 정리되어 있다. 이 장의 목표는 새로운 전파 환경에서 적정 전파거리 d'을 ASM 방식과 BL-ASM 방식을 이용해서 유도하는 것이다.
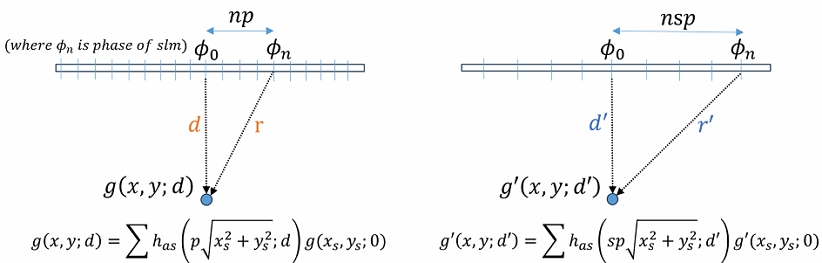
(left) For a pixel pitch of p and a propagation distance of d, the distance between the location corresponding to g(x, y;d) and an arbitrary point ϕn on the SLM is denoted as r' (Right) When the pixel pitch changes to sp, at a propagation distance of d', the distance between the location corresponding to g'(x, y;d) and an arbitrary point ϕn on the SLM is denoted as r' The goal of this paper is finding optimal d'
1. ASM 방식을 이용해서 적정 전파거리를 유도
g'(x, y;d)는 새로운 SLM 평면을 나타내는 함수이다. 앞서 계산의 편의를 위해서 좌표 (x, y)는 실제 물리적 거리가 아닌 상대적 거리로 표현한 것을 기억할 것이다. 이전 SLM 평면의 wavefield를 나타내는 g(x, y;d)과 새로운 SLM의 평면을 나타내는 g'(x, y;d)에서 각 함수의 (x, y)좌표에 대응하는 물리적 위치와 (x + 1, y)에 대응하는 물리적 위치 사이의 거리는 화소 간격이 늘어난 만큼 s배 늘어났다. 하지만 같은 위상 홀로그램 신호를 입력했기 때문에 두 식의 같은 (x, y)좌표에서의 값은 같다. 때문에 (13)과 같이 나타낼 수 있다.
| (13) |
하지만, 전파 커널 hAS의 매개변수는 달라진다. 전파 커널의 수식인 (6)에서 w는 실제 SLM 평면 위에서의 물리적 거리에 해당하는 값이다. 그러므로, 새로운 SLM의 전파 환경을 모사하기 위해서는 전파 커널의 변수 w에 s배 곱해진 값을 대입해야 한다. 그러므로 (8)과 마찬가지로 새로운 SLM 평면인 g'(x, y;d)으로부터 d'만큼 떨어진 wavefield인 g'(x, y;d')은 (10)과 같이 계산할 수 있다.
| (14) |
서론에서 언급했듯, 픽셀피치가 달라졌을 때 기존과 같은 전파거리 d에서 수치적 복원을 한 결과는 목표 이미지와는 무관한 잡음처럼 보인다. 본 연구의 목표는 SLM의 환경 설정이 달라지더라도 의도한 목표 이미지가 관측되는 전파거리 d'을 계산하는 것이다. 즉 (15), (16)을 만족시키는 d'을 찾는 것이 목표다.
| (15) |
| (16) |
홀로그램의 전파거리가 늘어나면, 전자기파의 세기가 약해지기 때문에 이미지의 밝기는 줄어들 수밖에 없다. (15), (16)에서 σ는 밝기를 맞춰주기 위한 상수 스케일 값을 의미한다. 절댓값을 취하는 이유는, 목표 이미지의 위상이 아닌 진폭의 분포가 일치하는 것이 목표이기 때문이다.
(5)의 r과 d는 실제 디스플레이 환경에서는 거의 같다 (r ≃ d). 그러므로 hAS의 진폭의 크기는 전파거리 d에 반비례한다고 할 수 있다. 즉 (17)이 성립한다.
| (17) |
(15), (16)에서 σ는 스케일을 맞추기 위한 값이므로, σ = d/d'를 대입하면 양변의 크기를 맞춰줄 수 있다. (16)의 양변의 진폭의 크기가 같으므로 (5)의 위상 부분만을 이용해서 (16)을 다시 적으면 (18)을 만들 수 있다.
(18)에서 좌변과 우변을 각각 전개해보면 모든 복소수 항의 크기는 같고 복소수 항의 개수도 같다. 그러므로 각 변에서 첫 번째 복소수 항의 위상과 n번째 임의의 복소수 항의 위상의 차이가 일정하게 유지된다면, (18)은 항상 성립한다. 즉 (19)를 만족하면 (18)은 성립한다.
| (18) |
(19)에서 ϕ0,ϕn은 그림 2에서 표현된 것처럼 각각 g(x, y;0)에서 직선거리에 있는 복소진폭의 위상과 임의의 거리 n만큼 떨어져 있는 위치에서 복소진폭의 위상을 나타낸다. (19)에서 k = 2π/λ로 매우 큰 숫자이므로, 위의 수식의 arctan(*)는 전부 π/2로 근사할 수 있다. 자세한 근사 정보는 Ⅳ장에 있다. ϕ0와 ϕn에 해당하는 위치의 상대적 거리를 wn이라 하고, 수식을 정리하면 (20)을 얻을 수 있다.
| (19) |
| (20) |
(20)을 만족하는 d'을 계산하면, 픽셀피치가 sp인 다른 SLM 장치에서 원하는 목표 이미지가 조합되는 거리 d'을 구할 수 있다. 이때 (20)을 만족하는 d'은 (21)의 결과와 같다.
(21)에서 d가 pwn에 비해 매우 크기 때문에, 실용적인 환경에서 SLM의 픽셀피치가 s배 커지면, 목표 이미지가 조합되는 거리는 약 s2배 만큼 늘어난다고 정리할 수 있다.
| (21) |
2. BL-ASM 방식에서의 유효성 증명
Ⅱ장 2절에서 BL-ASM 방식은 ASM 방식의 결과에 저주파 필터를 씌운 것과 같은 효과를 준다고 언급했다. 여기에 사용되는 sinc(•)함수를 자세히 분석해보면, 픽셀피치가 바뀐 상황에서도 유사한 결과를 주는 것을 알 수 있다. 이 절에서는 픽셀피치가 p인 환경과 sp인 환경에서 BL-ASM 방식의 대역폭 제한이 유사한 효과를 가짐을 증명할 것이다.
(10)에 사용된 Δu,Δv는 (22)로 정의된다[6].
| (22) |
(22)에서 Δx,Δy는 각각 wavefield의 표본화 주기, 즉 픽셀피치의 크기이다. M, N은 각각 x축과 y축의 홀로그램 해상도를 의미한다. 그러므로 MΔx,NΔy는 각각 홀로그램의 x축과 y축 방향의 물리적인 크기를 나타낸다. 픽셀피치가 p인 원본 홀로그램의 x축 방향 길이를 W라고 하면, 픽셀피치가 sp인 새로운 홀로그램의 x축 방향 길이는 sW이다. 이와 함께 1절의 유도 결과인 d' = s2d를 (10)에 대입해서, 원본 전파 환경의 주파수 영역의 최댓값인 uBLori와 새로운 전파 환경의 주파수 영역의 최댓값인 uBLnew을 계산하면 (23), (24)와 같이 유도할 수 있다.
| (23) |
| (24) |
그러므로 2d ≫ W인 환경에서는 (25)가 성립한다. 근사조건에 관해서는 Ⅳ장에서 자세히 다룰 것이다.
| (25) |
(11)의 저주파 필터로 쓰이는 2uBLsinc(2uBLx)도 (25)를 이용해서 각각의 환경에 계산할 수 있다. (25)에서 uBLnew가 uBLori의 배이므로 2uBLnewsinc(2uBLnewx)의 함수의 폭은 2uBLorisinc(2uBLorix)에 비해 s배 커진다. 이는 픽셀피치가 s배 커진 새로운 전파 환경에 비례하는 결과이다. 결론적으로 픽셀피치가 p에서 sp가 되었을 때, 1절의 결과를 만족하는 전파거리라면, BL-ASM의 대역폭 제한의 결과는 같다. 때문에 BL-ASM 방식으로 적정 전파거리를 계산하여도 1절의 결과와 똑같은 결과를 유도할 수 있다.
Ⅳ. 근사조건 고찰
Ⅲ의 전개과정에서 사용된 근사조건은 arctan(kd) = π/2, d ≃ r 이다. 이 중에서 arctan(kd) = π/2의 경우 λ = 520nm라면, k ≃ 1.2×107이므로 거의 항상 성립한다. d ≃ r조건의 경우 프레넬 근사가 유효한 거리라면 성립한다는 것이 알려져 있다[6].
일반적으로 근거리 전파를 근사할 때 사용하는 근사는 프레넬 근사이다. 프레넬 근사의 경우 (26)을 만족하는 거리에서 유효하다는 것이 알려져 있다[7].
| (26) |
(26)에서 (x-ξ)2 + (y-η)2는 개구면의 최대 크기의 제곱이다. [8]에서는 프레넬 근사 조건을 만족한면 d ≃ r라고 할 수 있다고 언급하고 있다. 그러므로 프레넬 근사가 적용되는 거리보다 먼 상황에서는 본 논문의 전개 과정이 타당하다고 할 수 있다. 또한 프레넬 근사가 유효하지 않은 가까운 거리라도 d ≃ r을 만족한다면 유효한 결과를 보여주는 것을 알 수 있다. 이는 Ⅴ장에서 실험적으로 확인할 것이다.
Ⅴ. 실험 결과 및 분석
본 장에서는 앞선 Ⅲ장의 유도 결과와 Ⅳ장의 근사조건을 실험적으로 검증할 것이다. 1절에서는 프레넬 근사조건이 유효한 전파 환경에서 픽셀피치가 2배 증가했을 때, Ⅲ장의 유도 결과인 4d에서 목표 이미지가 잘 보이는지를 검증할 것이다. 자세한 검증을 위해서 목표 거리를 포함해서 더 가까운 거리와 먼 거리까지 40개의 전파 거리에 대해서도 추가로 목표 이미지와의 유사성을 검증할 것이다. 2절에서는 프레넬 근사조건보다 더욱 가까운 거리에서도 Ⅳ장의 근사조건을 만족한다면 Ⅲ장의 유도 결과가 유효함을 보일 것이다.
실험에 사용된 이미지는 각 실험 모두 800장이며, 사용된 데이터셋은 DIV2K training dataset[8]이다. 각각의 실험에 사용된 목표 이미지는 위상 홀로그램은 모두 SGD 방법으로 생성하였다.
1. 전파거리에 따른 목표 이미지와의 유사성 분석
Ⅳ에서 프레넬 근사가 유효한 거리라면, 본 논문의 계산 결과가 유효함을 언급했다. 이 절에서는 (26)의 수식을 만족하는 조건에서 본 논문의 계산 결과가 유효함을 실험적으로 검증할 것이다. SLM의 픽셀피치가 6.3μm, 해상도가 1K라고 한다면, 개구면의 최대 크기는 대략 0.89cm이다. 이 수치를 파장의 길이 530nm와 함께 (26)에 대입하여 구한 전파거리 d는 약 20cm이다. 이 절에서는 이 조건을 만족하는 전파거리에서 본 논문의 전파거리 유도가 유효함을 검증할 것이다.
이 절의 실험에 사용하는 위상 홀로그램은 픽셀피치 6.4μm, 파장 520nm, 전파거리 20cm에 최적화하여 SGD 방법으로 만들었다. 그리고 이 위상 홀로그램을 픽셀피치가 두 배인 12.8μm로 바뀐 환경에서 전파거리를 변화시켜가며 BL-ASM 방식으로 수치적 복원했다. Ⅲ의 계산 결과가 옳다면 원래 전파거리의 4배인 80cm 근처에서 가장 복원이 잘되어야 한다. 그림 3은 800개 홀로그램 데이터의 복원된 이미지와 원본 이미지와의 평균 Peak Signal-Noise Ratio (PSNR)을 계산하여 전파거리별로 나타낸 그래프이다. 유도된 대로 픽셀피치가 늘어난 비율의 제곱 배 거리인 80cm에서 원본과의 PSNR이 24.0561으로 가장 유사한 이미지가 보이는 것을 확인할 수 있다. 또한 유도된 적정 전파 거리인 80cm보다 더 멀거나 가까울수록 PSNR 또한 낮아지는 것도 적정 전파 거리에 신뢰성을 더해준다.
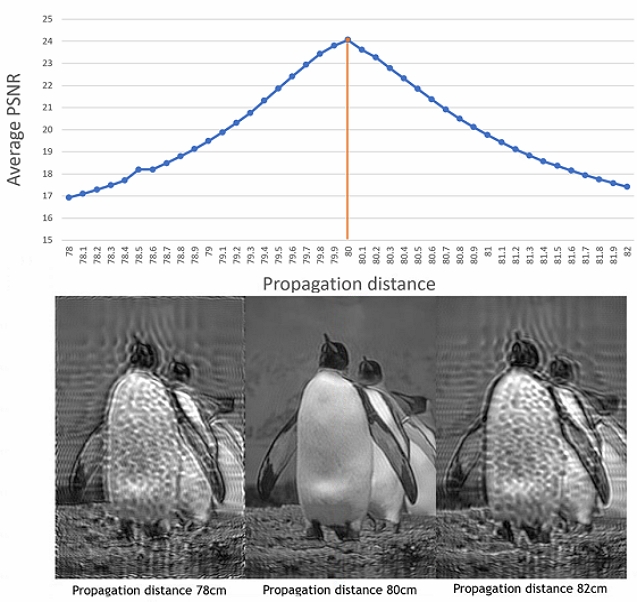
(up) As 800 holograms optimized for pixel pitch of 6.4μm, wavelength of 520nm, and propagation distance of 20cm are numerically reconstructed with pixel pitch of 12.8μm, a graph showing the average PSNR values with the target image depending on the propagation distance (down) Numerically reconstructed images at each distance of 78cm, 80cm, and 82cm
개별 이미지 분석으로는, 800개의 이미지 중에서 대다수인 780개의 이미지가 유도한 전파거리인 80cm에서 원본 이미지와의 PSNR이 가장 높은 것을 확인할 수 있었다. 나머지 20개의 이미지 또한 전부 80.1cm에서 PSNR이 가장 높았는데, 이는 (21)의 결과를 엄밀히 따져보면 전파거리의 증가 비율이 s2보다 미세하게 높기 때문으로 분석된다. 결과적으로 이 절의 실험은 프레넬 근사가 유효한 거리에서 본 논문의 적정 전파거리 유도가 성립함을 검증했다.
2. 근사조건의 유효성 실험
본 논문의 유도과정에서 사용한 근사조건은 d ≃ r이다. 즉, 프레넬 근사가 유효하지 않은 매우 가까운 전파 거리이더라도 d ≃ r만 만족한다면 본 논문의 계산 결과가 유효하다고 할 수 있다. 이 절에서는 d ≃ r을 만족하는 매우 가까운 거리에서 본 논문에서 유도한 적정 거리에서 깨끗한 이미지가 보이는 지를 검증할 것이다. 검증 방법은 1절과 유사하게 유도된 적정 전파거리로부터 가깝거나 먼 40개의 전파거리에서 목표 이미지와의 PSNR을 계산할 것이다.
개구면의 최대 크기가 0.89cm, d가 1cm라면 r의 최댓값은 1.3cm로 거리 d와 유사하다. 이 절에서 사용하는 위상 홀로그램은 픽셀피치 6.4μm, 파장 520nm, 전파거리 1cm에 최적화되어 SGD 방법으로 만들어졌다. 그림 4는 근거리 전파에 최적화되어 만들어진 이 위상 홀로그램을 1절의 실험과 마찬가지로 픽셀피치를 2배로 늘린 뒤, 전파거리를 변화해 가며 BL-ASM 방식으로 수치적 복원한 결과이다. 그림 4를 보면 매우 가까운 전파거리에서 만들어진 홀로그램이더라도 계산된 전파거리인 4cm에서 가장 높은 평균 PSNR인 24.7286을 보여주는 것을 확인할 수 있었다. 또한 유도된 거리에서 0.1cm 가까워지거나 멀어지기만 해도 10dB정도 떨어지는 것도 확인할 수 있었다. 이는 매우 가까운 거리 최적화되어 만들어진 홀로그램이기 때문에 거리 변화에 민감한 것으로 해석된다. 또 개별 이미지 분석으로는, 800개의 이미지 모두 유도된 거리에서 가장 높은 PSNR 수치를 보이는 것을 확인할 수 있었다.
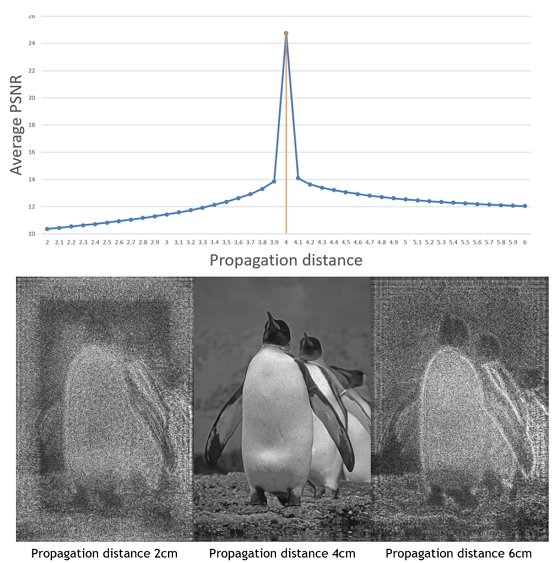
(up) As 800 holograms optimized for pixel pitch of 6.4μm, wavelength of 520nm, and propagation distance of 1cm are numerically reconstructed with pixel pitch of 12.8μm, a graph showing the average PSNR values with the target image depending on the propagation distance (down) Numerically reconstructed images at each distance of 2cm, 4cm, and 6cm
Ⅵ. 결 론
본 논문에서는 위상 홀로그램을 one-source multi-use 환경에서 이용하기 위한 기반 연구로서 특정한 픽셀피치의 SLM을 목표로 생성한 홀로그램을 다른 픽셀피치의 SLM에서도 올바르게 재현하기 위한 적정 전파거리를 수학적으로 유도하고 실험적으로 검증했다. 수학적 유도 결과로는, 디스플레이 환경에서 픽셀피치가 s배만큼 변하면 적정 전파거리는 약 s2배만큼 변하는 것을 유도할 수 있었다. 또 BL-ASM 수치적 복원을 이용해서 실험적으로 유도 결과를 증명해보았다. 더불어 프레넬 근사의 유효범위가 아닌 매우 가까운 전파거리에서도 계산이 유효함을 실험적으로 증명했다. 본 연구는 하나의 콘텐츠를 서로 다른 환경의 SLM에서 디스플레이할 때에 고려해야 할 사항인 적정 전파거리를 계산하는 방법을 제시하고 증명했다. 본 연구가 바탕이 되어 홀로그램 콘텐츠 확산에 도움이 될 수 있을 것이다.
Acknowledgments
This work was supported by Samsung Research Funding & Incubation Center of Samsung Electronics under Project Number SRFC-IT2201-03.
This research was supported by the MSIT(Ministry of Science and ICT), Korea, under the National Program for Excellence in SW)(2023-0-00042) supervised by the IITP(Institute of Information & Communications Technology Planning&Evaluation) in 2023.
References
-
ZHANG, Zichen; YOU, Zheng; CHU, Daping. Fundamentals of phase-only liquid crystal on silicon (LCOS) devices. Light: Science & Applications, Vol.3, No.10, e213-e213, 2014.
[https://doi.org/10.1038/lsa.2014.94]

-
MAIMONE, Andrew; GEORGIOU, Andreas; KOLLIN, Joel S. Holographic near-eye displays for virtual and augmented reality. ACM Transactions on Graphics (Tog), Vol.36, No.4: pp.1-16, 2017.
[https://doi.org/10.1145/3072959.3073624]

- GERCHBERG, Ralph W. A practical algorithm for the determination of plane from image and diffraction pictures. Optik, Vol.35, No.2, pp.237-246, 1972.
-
PENG, Yifan, et al. Neural holography with camera-in-the-loop training. ACM Transactions on Graphics (TOG), Vol.39, No.6, pp.1-14, 2020.
[https://doi.org/10.1145/3414685.3417802]

-
MATSUSHIMA, Kyoji; SHIMOBABA, Tomoyoshi. Band-limited angular spectrum method for numerical simulation of free-space propagation in far and near fields. Optics express, Vol.17, No.22 pp19662-19673, 2009.
[https://doi.org/10.1364/oe.17.019662]

- Matsushima, K. Introduction to Computer Holography. Series in Display Science and Technology. pp.83-86, 2020.
- J.W. Goodman "Introduction to Fourier optics, Third Edition", pp.66-69, 2005.
-
AGUSTSSON, Eirikur; TIMOFTE, Radu. Ntire 2017 challenge on single image super-resolution: Dataset and study. In: Proceedings of the IEEE conference on computer vision and pattern recognition workshops. pp 126-135, 2017.
[https://doi.org/10.1109/cvprw.2017.150]


- 2019년 3월 ~ 현재 : 경희대학교 컴퓨터공학과 학사
- ORCID : https://orcid.org/0009-0006-3829-160X
- 주관심분야 : 영상처리 및 패턴인식, 홀로그래피, 인공지능

- 2023년 2월 : 경희대학교 소프트웨어융합학과 학사
- 2023년 3월 ~ 현재 : 경희대학교 컴퓨터공학과 석사
- ORCID : https://orcid.org/0000-0002-3613-3847
- 주관심분야 : 영상처리 및 패턴인식, 홀로그래피, 인공지능

- 2022년 8월 : 경희대학교 소프트웨어융합학과 학사
- 2024년 2월 : 경희대학교 컴퓨터공학과 석사
- 2024년 3월 ~ 현재 : 경희대학교 컴퓨터공학과 박사
- ORCID : https://orcid.org/0000-0002-6402-7785
- 주관심분야 : 영상처리 및 패턴인식, 홀로그래피, 인공지능, 비디오 부호화

- 2021년 8월 : 경희대학교 소프트웨어융합학과 학사
- 2021년 9월 ~ 2023년 8월 : 경희대학교 컴퓨터공학과 석사
- ORCID : https://orcid.org/0000-0001-5322-3556
- 주관심분야 : 영상처리 및 패턴인식, 홀로그래피, 인공지능, 비디오 부호화

- 1994년 8월 : KAIST 전기및전자공학과 공학사
- 1998년 2월 : KAIST 전기및전자공학과 공학석사
- 2004년 2월 : KAIST 전기및전자공학과 공학박사
- 2003년 8월 ~ 2005년 10월 : ㈜애드팍테크놀러지 멀티미디어팀 팀장
- 2005년 11월 ~ 2019년 8월 : 한국전자통신연구원(ETRI) 실감AV연구그룹 그룹장
- 2013년 9월 ~ 2014년 8월 : Univ. of Southern California (USC) Visiting Scholar
- 2019년 9월 ~ 2020년 2월 : 숙명여자대학교 전자공학전공 부교수
- 2020년 3월 ~ 현재 : 경희대학교 컴퓨터공학과 부교수
- ORCID : https://orcid.org/0000-0001-7308-133X
- 주관심분야 : 비디오 부호화, 딥러닝 영상처리, 디지털 홀로그램

