표면 추정 및 이상치 제거 기반 포인트 클라우드 밀도 품질 평가 고도화
Copyright © 2023 Korean Institute of Broadcast and Media Engineers. All rights reserved.
“This is an Open-Access article distributed under the terms of the Creative Commons BY-NC-ND (http://creativecommons.org/licenses/by-nc-nd/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited and not altered.”
초록
3차원 영상의 손실 압축에서는 위치 정보 압축 왜곡이 발생하며, 위치 정보의 왜곡은 속성 정보의 왜곡을 동반하기 때문에, 위치 정보의 압축 왜곡을 다양한 측면에서 판단하는 것은 매우 중요하다. 특히, 포인트 클라우드에서는 점 위치의 이동으로 발생하는 왜곡뿐만 아니라, 점 개수가 변경되는 밀도 왜곡이 발생할 수 있다. 이러한 밀도 왜곡을 정량적으로 평가하기 위해 D3-PSNR과 ‘밀도 적응적 왜곡 결정’이 제안되었다. 하지만, D3-PSNR은 포인트 클라우드의 표면을 부피를 기반으로 추정하므로, 근사값이 실제 표면적과 크게 다르다는 한계점이 있으며, ‘밀도 적응적 왜곡 결정’ 방식은 점이 1~2개만 존재하는 초저밀도 영역에서 발생하는 왜곡에 민감하게 반응하는 한계가 존재한다. 따라서, 본 논문은 기존의 포인트 클라우드 밀도 품질 평가 방안들의 한계점을 상세히 제시하고, 이를 극복하기 위한 표면 추정 및 이상치 제거 기반 포인트 클라우드 밀도 품질 평가 방안을 제안한다. 제안 기술은 기존 포인트 클라우드 밀도 평가 기술의 제한 사항인 단위 반경의 부정확도와 초저밀도 데이터에서의 한계를 극복하였으며, 이는 실험 결과를 통해 검증되었다.
Abstract
In the lossy compression of 3D media, there is compression distortion in position information, and since position distortion is accompanied by distortion in attribute information, it is very important to evaluate distortion of position information in terms of various aspects. Particularly in point clouds, distortion can occur not only due to changes in the position of points but also due to density distortion caused by variations in the number of points. To quantitatively evaluate this density distortion, D3-PSNR and ‘density adaptive distortion determination’ were proposed. However, since D3-PSNR estimates the surface of the point cloud based on its volume, it has the limitation that the approximate value is significantly different from the actual surface area. Additionally, the 'density-adaptive distortion determination' method is sensitive to distortion occurring in extremely low-density regions where only 1 or 2 points exist. Therefore, this paper presents in detail the limitations of conventional point cloud density quality evaluation methods and proposes a point cloud density quality evaluation method based on surface estimation and outlier removal to overcome these limitations.
Keywords:
Density quality evaluation, Density distortion, Point Cloud, D3-PSNR, AI-PCCⅠ. 서 론
기존의 2차원 영상은 해상도에 따라 영상이 갖는 픽셀의 개수가 결정되므로, 영상의 해상도(너비x높이)와 각 픽셀의 값들로 2차원 영상을 완벽하게 표현할 수 있다. 하지만, 3차원 영상은 해상도 영역 내 빈공간이 존재하기 때문에, 객체의 점유 영역과 빈공간을 구분하고 객체 속성 정보(색상, 반사율 등)를 표현하기 위해서는 위치 정보와 속성 정보가 모두 필요하다. 이에, 3차원 영상은 3차원 위치 값과 속성 값을 갖는 점의 집합으로 표현되며, 이러한 점의 집합으로 구성된 데이터를 포인트 클라우드라고 한다[1]. 3차원 포인트 클라우드 영상은 2차원 영상에 비해 해상도가 증가할수록 데이터의 크기가 급격히 증가하므로, 포인트 클라우드 영상의 전송 및 소비를 위해서는 효과적인 압축 방식이 필수적이다[2]. 특히, 데이터의 왜곡을 감수하고 높은 압축률을 획득하는 손실 압축 기법은 적은 대역폭을 사용하면서도 많은 양의 데이터를 전송할 수 있다는 점에서 대단히 효율적인 압축 방식이다[3]. 하지만, 손실 압축 시에는 압축률의 증가에 따라 데이터의 왜곡 또한 증가하므로, 손실 압축의 성능을 판단하기 위해서는 압축률과 압축 왜곡의 관계를 함께 파악하여야 한다.
속성 정보에 대한 압축 왜곡만 일어나는 2차원 영상의 손실 압축과는 달리, 3차원 영상의 손실 압축에서는 위치 정보 압축 왜곡이 발생한다[3]. 특히, 위치 정보의 왜곡은 속성 정보의 왜곡을 동반하기 때문에[4], 위치 정보의 압축 왜곡을 다양한 측면에서 판단하는 것은 매우 중요하다. 이에, 국제 표준화 기구인 ISO/IEC JTC1/SC29/WG7 3DGH (3D Graphics and Haptics)에서는 D1-PSNR(Peak Signal-to-Noise Ratio)과 D2-PSNR을 사용하여 위치 정보 왜곡을 평가한다[5]. D1-PSNR은 원본 점과 복호화된 점의 거리를 비교하여 위치 정보 왜곡을 계산하며, D2-PSNR은 원본 점이 이루고 있는 평면과 복호화된 점 사이 거리를 비교하여 위치 정보의 왜곡을 계산한다. 따라서, D1-PSNR과 D2-PSNR을 활용하여 위치 정보의 왜곡을 점의 공간상의 이동과 평면상의 이동 측면에서 모두 평가할 수 있다. 하지만 3차원 위치 정보에서는 이와 같은 점 위치의 이동으로 발생하는 왜곡에 대한 평가뿐만 아니라, 2차원 영상과는 달리 점 개수에 대한 왜곡, 즉, 밀도 왜곡이 발생할 수 있다.
밀도 왜곡은 포인트 클라우드가 속한 공간 전반에 걸쳐 발생할 수도 있으며, 특정 영역에서만 집중적으로 발생할 수도 있다. 공간 전반에 걸쳐 발생한 밀도 왜곡은 포인트 클라우드의 해상도 저하와 유사한 효과를 나타내며[6], 특정 영역에 집중된 밀도 왜곡은 객체 표면에 홀(Hole)을 발생시킨다[7]. 이러한 밀도 왜곡을 정량적으로 평가하기 위해 원본 포인트 클라우드와 복호화된 포인트 클라우드 사이에서 각 점의 밀도를 비교하는 밀도 품질 평가 방안인 D3-PSNR[7]이 제안되었다. 하지만, D3-PSNR은 포인트 클라우드 콘텐츠들의 밀도 특성에 따라 적응적으로 동작하지 못한다는 한계점이 있어, 밀도 왜곡 평가 수치의 일반화가 어렵다는 문제가 존재한다. 이러한 문제를 해결하기 위해 ‘밀도 적응적 왜곡 결정’ 방식이 제안되었으나, 밀도 적응적 왜곡 결정 기반 기술은 점의 손실률로 밀도 왜곡을 판단하기 때문에, 1~2개의 점이 존재하는 영역에서 발생하는 왜곡에 민감하게 반응하는 한계가 존재한다[8]. 따라서, 본 논문은 기존의 포인트 클라우드 밀도 품질 평가 방안들의 한계점을 상세히 제시하고, 이를 극복하기 위한 표면 추정 및 이상치 제거 기반 포인트 클라우드 밀도 품질 평가 방안을 제안한다.
본 논문의 구성은 다음과 같다. Ⅱ장에서는 포인트 클라우드 밀도 품질 평가를 위한 관련 연구들에 대해 설명한다. Ⅲ장에서는 기존 연구들의 한계점을 설명하고, 이를 극복하기 위한 표면 추정 및 이상치 제거 기반 포인트 클라우드 밀도 품질 평가 방안에 대해 제안한다. Ⅳ장에서는 실험 결과를 통해 제안한 밀도 품질 평가 방안을 검증하며, 마지막으로, Ⅴ장에서는 제안 기술에 대한 결론으로 본 논문을 맺는다.
Ⅱ. 포인트 클라우드 밀도 품질 평가 관련 연구
포인트 클라우드 밀도 품질 평가에 대한 필요성은 인공지능을 활용한 포인트 클라우드 압축 방식 개발로 대두되었다. 인공지능을 활용한 AI-PCC(Artificial Intelligence-based Point Cloud Compression)[9]는 기존 포인트 클라우드 압축 기술과 동일 압축률에서 비교 시 D1-PSNR, D2-PSNR 측면에서 유사하거나 더 높은 성능을 달성하였다[10][11][12][13]. 하지만, 복호화된 포인트 클라우드의 특정 영역에서 밀도가 급격히 저하되는 현상으로 인해 그림 1과 같이 홀이 발생하는 등 주관적 평가에서 품질을 보장하기 어려웠다.
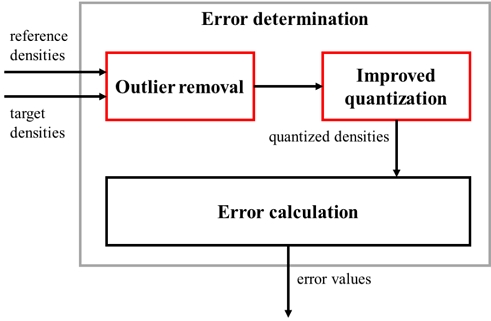
이에, 원본 포인트 클라우드와 복호화된 포인트 클라우드의 밀도 왜곡 정도를 정량적으로 나타내고, 밀도 품질을 객관적으로 비교하기 위한 D3-PSNR이 제안되었다[7]. D3-PSNR은 밀도 품질 평가의 기준이 되는 참조(Reference) 포인트 클라우드와 밀도 평가 대상인 대상(Target) 포인트 클라우드의 밀도를 PSNR 값으로 비교하며, 그림 2와 같은 구조로 설계되어 있다.
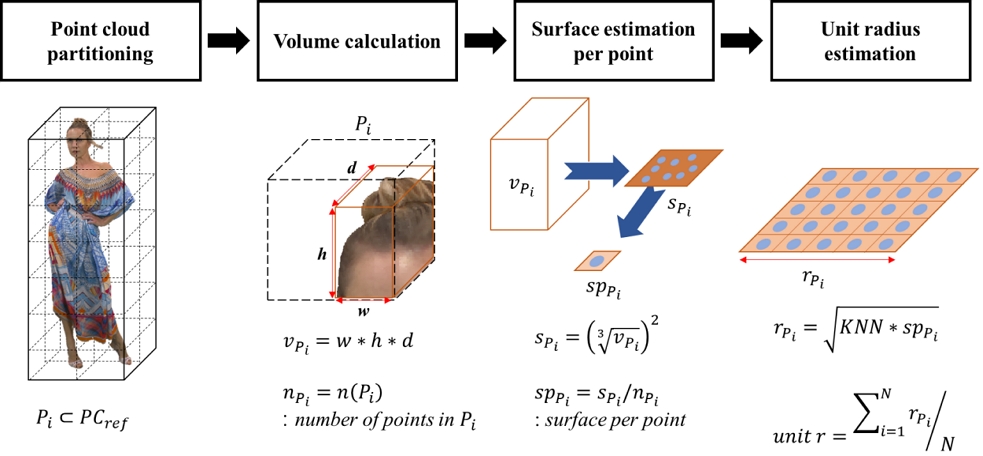
먼저, 그림 2의 밀도 추정(Density estimation) 모듈에서는 포인트 클라우드 내 각 점의 위치마다 주변 공간의 밀도를 계산하며, 밀도는 단위 부피 당 존재하는 점의 수를 통해 계산된다. 포인트 클라우드 콘텐츠는 표현 대상 혹은 취득 방식에 따라 밀도 특성이 다르기 때문에, 단위 부피의 크기는 포인트 클라우드 콘텐츠의 밀도 특성을 고려하여 결정되어야 한다. 따라서, D3-PSNR은 최근접 이웃 점의 개수(KNN, K-Nearest Neighbor)를 사전 설정하고, 포인트 클라우드 내에서 평균적으로 KNN 개의 점을 도출할 수 있는 단위 부피를 추정하여 각 점의 밀도를 계산한다. D3-PSNR에서 단위 부피는 단위 반경을 추정한 뒤 구의 부피 공식을 통해 획득되며, 단위 반경의 추정 과정은 그림 3과 같다.
단위 반경은 참조 포인트 클라우드(PCref)를 여러 개의 파티션(Pi,)으로 분할한 뒤, 각 파티션에서 획득된 반경의 평균을 계산하는 것으로 추정된다. 이를 위해, 포인트 클라우드 파티셔닝(Point cloud partitioning) 단계에서는 사전 정의된 파티션 분할 계수(Cpart)로 참조 포인트 클라우드를 동일한 크기를 갖는 N 개의 정육면체로 분할한다. Cpart는 참조 포인트 클라우드 점유 공간 중 가장 긴 축의 분할 횟수를 나타내므로, 파티션의 크기는 참조 포인트 클라우드의 크기에 따라 다르게 결정된다. 그 후, 부피 계산(Volume Calculation) 단계에서는 파티션 내에 점이 존재하는 점유 공간의 크기(vPi)와 파티션에 존재하는 점의 수(nPi)를 계산하고, 점 당 표면 추정(Surface estimation per point) 단계에서는 vPi 값을 2차원 표면적(sPi)으로 근사한 뒤, 한 점이 차지하고 있는 표면의 크기(spPi)를 계산한다. 부피가 아닌 표면의 크기로 단위 반경을 추정하는 이유는, 포인트 클라우드의 점들은 객체의 표면에만 존재하기 때문이다. 단위 반경 추정(Unit radius estimation)에서는 각 파티션 내에서 KNN 개의 점이 갖게 되는 반경(rPi)을 spPi로부터 계산하고, rPi의 평균으로 참조 포인트 클라우드의 단위 반경(unit r)을 추정한다.
D3-PSNR에서는 이러한 방식 외에도, 파티셔닝을 수행하지 않고 포인트 클라우드 전체 영역으로 단위 반경을 계산하는 ‘전역 단위 반경 추정’, 그리고 참조 포인트 클라우드와 대상 포인트 클라우드에 서로 다른 단위 반경을 사용하는 ‘개별 단위 반경 추정’ 등을 사용해 단위 반경을 추정할 수 있다[14]. 하지만 본 논문에서는 그림 3에서 설명된 바와 같이, 참조 포인트 클라우드의 부분영역 밀도를 고려하는 ‘지역 단위 반경 평균 추정’과 참조 포인트 클라우드와 대상 포인트 클라우드에서 동일한 반경으로 밀도 왜곡을 계산하는 ‘동일 단위 반경 추정’ 기술을 이용한다.
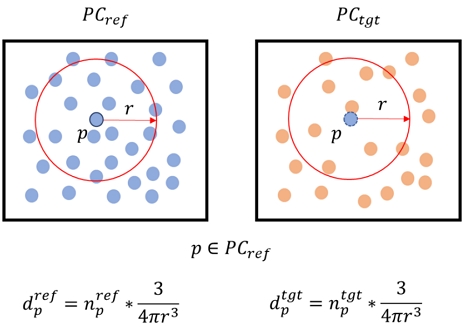
계산된 참조 포인트 클라우드의 단위 반경은 대상 포인트 클라우드의 밀도 계산에도 동일하게 사용되며, D3-PSNR은 그림 4와 같이 참조 포인트 클라우드 내 각 점의 위치를 기준으로 참조 포인트 클라우드 및 대상 포인트 클라우드 내에서 밀도를 계산한다.
그림 4의 r 은 단위 반경, 와 는 참조와 대상 포인트 클라우드(PCref, PCtgt)에서 탐색된 최근접 이웃 점의 수를 각각 나타낸다. 최근접 이웃의 탐색은 PCref의 한 점 p의 위치를 기준으로 수행된다. D3-PSNR은 와 를 획득하기 위해 시간 복잡도에서 높은 효율성(O(logn))을 갖는 K-D 트리의 최근접 탐색 방법[15]을 이용하며, PCref와 PCtgt를 K-D 트리로 각각 변환한 뒤 단위 반경(r) 범위에서 탐색을 수행한다. 획득된 와 를 탐색 범위의 부피()인 단위 부피로 나누면, 기준 위치(p)에서의 참조와 대상 포인트 클라우드 밀도(, )를 각각 계산할 수 있다. 최근접 이웃 탐색은 PCref의 모든 점이 기준 위치로 사용될 때까지 PCref와 PCtgt 내에서 각각 수행되므로, 참조와 대상 포인트 클라우드의 밀도 값 집합인 Dref()와 Dtgt()는 참조 포인트 클라우드의 점 개수와 동일한 개수의 원소를 갖게 된다.
계산된 참조 및 대상 포인트 클라우드의 밀도 값들은 그림 2의 오류 결정(Error determination) 모듈로 입력되어 밀도 왜곡 평가를 위한 오류 값을 획득하는데 이용된다. 먼저, 입력된 참조 및 대상 포인트 클라우드의 밀도 값들은 양자화를 통해 실수에서 정수로 변환된다. Dref와 Dtgt의 합집합인 D의 최솟값과 최댓값을 각각 minD, maxD라 한다면, 밀도의 양자화는 수식 (1)과 같이 표현된다.
| (1) |
round()는 반올림 함수이며, bitDepth는 사전 정의된 양자화 비트 수이다. 양자화는 Dref와 Dtgt의 모든 원소 내에서 일어나며, 양자화된 밀도 값()은 최대 2bitDepth-1 까지의 값을 갖게 된다. D3-PSNR은 양자화된 참조 및 대상 포인트 클라우드의 밀도 값(, )의 차이를 통해 오류 값을 계산하며, 오류 값(ep)들의 집합 E는 수식 (2)와 같이 표현된다.
| (2) |
앞서 밝힌 바와 같이, 와 는 모두 참조 포인트 클라우드 내 점 p의 위치를 기반으로 생성되었기 때문에 와 는 일대일 대응을 만족하며, 집합 E 또한 참조 포인트 클라우드 내 점의 개수와 동일한 개수의 원소를 갖게 된다.
그림 2의 D3-PSNR 계산(D3-PSNR calculation) 모듈에서는 밀도 오류 값들을 입력으로 받아 수식 (3)과 (4)에 나타난 바와 같이, 평균 제곱 오차(MSE, Mean Square Error)와 PSNR을 계산하여 D3-PSNR 값을 획득한다.
| (3) |
| (4) |
n(PCref)는 참조 포인트 클라우드 내 점의 개수, R은 양자화된 밀도의 최댓값(2bitDepth-1)이다. 수식 (4)를 통해 획득된 밀도 PSNR 값을 통해 대상 포인트 클라우드가 참조 포인트 클라우드와 얼마나 동일한 밀도를 유지하고 있는지 평가할 수 있으며, 품질 평가에서 널리 활용되는 PSNR 계산식을 사용하므로 결과값의 비교가 용이하다는 특징을 갖고 있다.
하지만, D3-PSNR은 저밀도와 고밀도 영역이 복합적으로 존재하는 포인트 클라우드의 품질을 평가하는 경우 고밀도 영역에서 발생하는 왜곡에 편향된 결과를 도출한다는 한계점이 존재한다. 이는, 밀도 계산 시 하나의 단위 부피 값이 사용되므로 계산된 밀도 값이 점 개수에 따라 결정되고, 참조 포인트 클라우드와 대상 포인트 클라우드 사이의 밀도 오류 값 또한 손실된 점의 개수로 결정되기 때문이다. 이로 인해 저밀도 영역에서는 점이 모두 사라지더라도 고밀도 영역에서 발생한 점 손실에 비해 작은 오류 값이 도출될 수 있다. 즉, 밀도 왜곡의 평가가 밀도의 절대값 크기에 의존적으로 결정된다. 이를 해결하기 위해 3DGH에 제안된 ‘밀도 적응적 왜곡 결정’ 방식은 수식 (5)에 나타난 바와 같이, 밀도 값들을 비율로 변경한다[8][16].
| (5) |
Eadt은 ‘밀도 적응적 왜곡 결정’ 방식의 오류 값(e'p)들의 집합을 의미한다. Dref와 Dtgt에 Dref의 값을 각각 나누어 참조 포인트 클라우드의 밀도는 ‘1’로 변환하고, 대상 포인트 클라우드의 밀도는 Dref 대비 Dtgt의 비율로 변환한다. 수식 (5)를 통해 ‘밀도 적응적 왜곡 결정’ 방식은 밀도 오류 값을 점 개수의 차이에서 비율의 차이로 변경할 수 있고, 고밀도 영역과 저밀도 영역에 적응적으로 밀도 왜곡을 평가할 수 있다.
앞서 살펴본, D3-PSNR과 ‘밀도 적응적 왜곡 결정’ 방식을 통해 포인트 클라우드의 밀도 품질을 객관적으로 비교하고, 밀도 왜곡을 정량적으로 평가할 수 있게 되었다. 하지만, D3-PSNR과 ‘밀도 적응적 왜곡 결정’ 방식 모두 대상 포인트 클라우드의 밀도 왜곡을 평가하는데 한계점을 지니고 있다. 이에, Ⅲ에서는 각 기술의 제한 사항을 밝히고, 제시한 한계점을 극복하기 위한 본 논문의 제안 기술을 설명한다.
Ⅲ. 표면 추정 및 이상치 제거 기반 밀도 품질 평가 고도화 방안
D3-PSNR은 포인트 클라우드의 표면을 파티션의 부피를 기반으로 추정하므로, 근사값이 실제 표면적과 크게 다르다는 한계점이 있으며, ‘밀도 적응적 왜곡 결정’ 방식은 점이 1~2개만 존재하는 초저밀도 영역에서 발생하는 왜곡에 민감하게 반응하는 한계가 존재한다. 따라서, 본 논문은 이러한 기존 밀도 품질 평가 방안의 한계를 극복하고 더 정확한 밀도 품질 평가를 수행하기 위해, 표면 추정 및 이상치 제거 기반의 포인트 클라우드 밀도 품질 평가 고도화 방안을 제안한다.
1. 표면 추정 기반 밀도 계산 고도화 방안
밀도 계산에 사용되는 단위 반경이 과소 혹은 과대하게 설정된다면, 부분영역에서 발생하는 밀도 변화를 감지하기 어려워지거나, 부분영역의 밀도 변화에 극히 민감해지게 된다. 따라서, 신뢰성 있는 밀도 품질 평가를 위해서는 단위 반경을 포인트 클라우드의 특성에 따라 정확하게 추정하여야 한다. D3-PSNR은 그림 3과 같이 파티션 내에서 점이 존재하는 공간의 부피(vPi)를 표면의 면적(sPi)으로 변환하여 단위 반경을 추정한다. 하지만 이와 같은 면적 추정 방식은 실제 포인트 클라우드의 표면보다 과소한 면적을 추정하게 된다. 또한, D3-PSNR은 단위 반경 계산 시 구의 부피로 사용되는 단위 반경을 정사각형의 한 변으로 추정하여 부정확한 값을 추정한다. 본 논문은 이러한 D3-PNSR의 한계점을 극복하고 보다 정확한 단위 반경을 추정하기 위해 ‘표면 추정 기반 밀도 계산 고도화’ 방안을 제안한다.
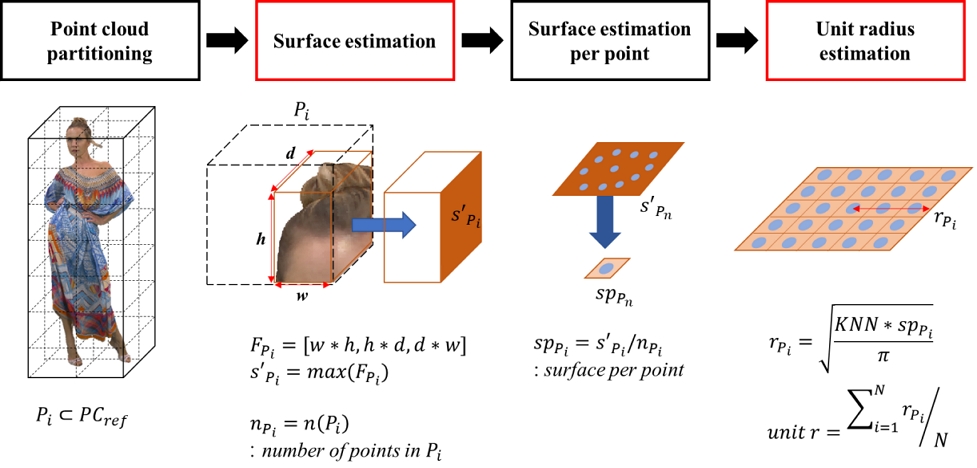
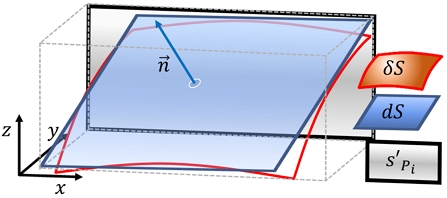
본 논문에서 제안하는 ‘표면 추정 기반 밀도 계산 고도화’ 방안은 그림 2의 밀도 추정(Density estimation) 모듈에서 수행된다. 먼저, 제안 기술은 D3-PSNR과 동일한 방식으로 참조 포인트 클라우드의 파티셔닝을 수행한다. 그 후, 본 논문에서 제안하는 그림 5의 표면 추정(Surface estimation) 단계는 파티션 내 점들이 이루고 있는 표면적을 추정한다. 이를 위해, 제안 기술은 파티션 내 점이 존재하는 육면체 공간의 3면 넓이(w*h, h*d, d*w)를 각각 계산한 뒤, 육면체 공간의 3면 넓이 집합(FPi) 내에서 가장 큰 값(max(FPi))을 표면적(s'Pi)으로 추정한다. 제안 기술을 통해 획득된 표면적 값은 포인트 클라우드의 곡면이 갖게 되는 표면적과 오차가 발생하게 된다는 점은 분명하나, 곡면 넓이의 선형 근사(Linear approximation)값을 추종하게 된다. 참조 포인트 클라우드를 잘게 파티셔닝 하여 생성된 미소 곡면을 δS라고 한다면, δS는 그림 6에서 보이는 바와 같이, 접평면 dS로 선형 근사할 수 있다[17].
이때, dS의 면적을 직접 계산하는 것은 몹시 높은 계산 복잡도가 요구되므로, dS의 면적 손실을 최소화하면서도 낮은 계산 복잡도로 표면적을 추정하기 위해 본 논문은 사영 평면의 면적을 이용한다. dS를 좌표계의 각 축(, , )으로 사영한다면, dS의 법선 벡터()와 좌표축의 내적 값이 가장 커지는 방향으로 사영하는 것이 dS의 면적 손실을 최소화 할 수 있다. 이때, 사영 평면은 dS 면적보다 항상 작거나 같은 값을 갖게 되므로[17], 각 좌표축의 사영 평면 중 최대 면적 값을 갖는 평면이 dS의 면적 손실을 최소화하는 사영 평면임을 의미한다. 이때, 본 논문의 제안 기술은 dS의 면적 손실을 보정하고 보다 간단하게 dS의 면적을 추정하기 위해, dS가 점유하고 있는 육면체의 넓이 집합(FPi) 중 가장 넓은 면적(max(FPi))을 표면적(s'Pi)으로 사용한다. 따라서, 제안 기술의 표면적 값은 곡면의 모양과 각도에 따라 오차가 발생하지만, 곡면 넓이의 선형 근사값을 추종하게 된다. 즉, 제안 기술은 3차원 부피를 2차원 면적으로 변환하는 기존 기술과 유사한 계산 복잡도로 보다 더 정확한 표면적 추정이 가능하다.
제안 기술을 통해 추정된 표면적(s'Pi)은 한 점이 차지하고 있는 표면의 크기(spPi)를 계산하는데 활용되며, spPi는 D3-PSNR의 점 당 표면 추정(Surface estimation per point) 단계와 동일한 방식으로 계산된다. 그 후 본 논문에서 제안하는 그림 5의 단위 반경 추정(Unit radius estimation) 단계에서는 원의 넓이 공식(πr2)을 통해 단위 반경을 도출한다. 따라서, 그림 5에서 보이는 바와 같이, KNN 개의 점이 갖게 되는 면적(KNN*spPi)에서 원주율(π)을 고려하여 반경(rPi)을 추정하고, rPi의 평균으로 참조 포인트 클라우드의 단위 반경(uinit r)을 계산한다.
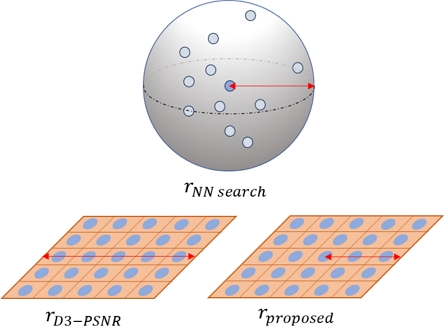
제안 기술의 단위 반경은 D3-PSNR의 단위 반경과 동일하게 최근접 이웃 탐색에서의 탐색 반경(rNN search)을 결정한다. 그림 7에서 보여지는 바와 같이, 최근접 이웃 탐색은 rNN search을 반지름으로 갖는 3차원 구 영역 안에 존재하는 모든 점을 찾는다. 기존의 D3-PSNR의 단위 반경(rD3-PSNR)은 정사각형의 넓이 공식으로 결정되기 때문에, 구의 반지름으로 사용할 경우 보다 과대한 영역을 탐색하는 한계가 있다. 하지만, 제안 기술은 원의 반지름으로 단위 반경(rproposed)을 추정하므로 구의 반지름과 정확히 대응된다. 따라서, 정사각형의 한 변으로 추정된 rD3-PSNR보다 제안 기술의 rproposed이 기하학적으로 더 타당함을 알 수 있다. 앞서 밝힌 바와 같이, 제안 기술은 rproposed를 통해 최근접 이웃을 탐색하고, 그림 4의 D3-PSNR 밀도 계산과 동일한 방식으로 참조 및 대상 포인트 클라우드의 밀도 값들을 추정한다.
2. 이상치 제거 및 개선된 양자화 기반 오류 결정 고도화 방안
Ⅱ장에서 밝힌 바와 같이, 저밀도와 고밀도 영역이 복합적으로 존재하는 포인트 클라우드 데이터의 품질을 평가하기 위해서는 ‘밀도 적응적 왜곡 결정’ 방식을 사용하여 고밀도 영역과 저밀도 영역에서 적응적으로 밀도 왜곡을 평가하여야 한다. 하지만, 해당 방식은 밀도 오류 값을 비율의 차이로 사용하기 때문에 점이 1~2개만 존재하는 초저밀도 영역에서 밀도 왜곡이 민감하게 반응하는 한계점을 갖고 있다. 이 뿐만 아니라, D3-PSNR이 수행하는 양자화는 밀도의 최솟값과 최댓값 범위를 항상 ‘0 ~ 2bitDepth-1’에 위치하도록 조정하므로, 밀도 값의 변화가 적을수록 밀도 값 범위가 크게 변경된다. 이로 인해, 밀도 품질 평가의 공정한 비교가 어렵다는 한계점이 존재한다. 따라서, 본 논문은 ‘이상치 제거 및 개선된 양자화 기반 오류 결정 고도화’ 방안을 제안하여 기존 포인트 클라우드 밀도 품질 평가의 한계를 극복하고자 한다.
본 논문에서 제안하는 ‘이상치 제거 및 개선된 양자화 기반 오류 결정 고도화’ 방안은 그림 2의 오류 결정(Error determination) 모듈에서 수행된다. 먼저, 그림 8의 이상치 제거(Outlier removal) 단계는 참조 및 대상 포인트 클라우드의 밀도 값들을 입력으로 받아, 사전 정의된 이상치 문턱 값 이하의 점 개수를 갖는 밀도 값들을 비교 대상에서 제거한다. 점 개수의 기준은 참조 포인트 클라우드의 밀도 값들이며, 수식 (6)과 (7)과 같이 밀도 값의 제거는 참조 및 대상 포인트 클라우드의 밀도 값들 모두에서 수행된다.
| (6) |
| (7) |
는 참조 포인트 클라우드(PCref)의 한 점, Oth는 이상치 문턱 값, 는 위치에서 단위 반경으로 탐색된 PCref 내 점의 개수, 와 는 각각 위치의 참조 및 대상 포인트 클라우드의 밀도 값, 와 는 각각 이상치 문턱 값 이하의 밀도 값이 제거된 참조 및 대상 포인트 클라우드의 밀도 값들을 의미한다. 입력 받은 참조 및 대상 포인트 클라우드의 밀도 값들(Dref, Dtgt)은 참조 포인트 클라우드의 모든 점 위치에 대한 밀도 값을 갖고 있지만, 수식 (6)과 (7)을 통해 Oth 이상의 값을 갖는 위치 밀도 값만이 와 에 저장된다. 따라서, 와 는 참조 포인트 클라우드의 점 개수보다 같거나 작은 원소 개수를 갖게 되며, 참조 포인트 클라우드의 를 기준으로 이상치 제거를 수행하기 때문에 일대일 대응 상태를 유지한다.
생성된 와 의 값들은 그림 8의 개선된 양자화(Improved quantization) 단계에서 정수로 변환된다. D3-PSNR의 양자화는 수식 (1)에서 확인된 바와 같이, 밀도 값들의 최솟값(minD)과 최댓값(maxD)을 모두 사용하는 일반적인 정규화(Normalization)을 수행하는데, 이 경우 서로 다른 대상 포인트 클라우드에서 발생한 밀도 손실을 비교하는데 제한점이 발생한다. 따라서, 본 논문은 밀도 오류 값의 동등한 비교를 위해 개선된 양자화 방안을 제안한다. 본 논문의 개선된 양자화는 최댓값만을 사용하여 양자화를 수행하며 수식 (8)과 같이 계산된다.
| (8) |
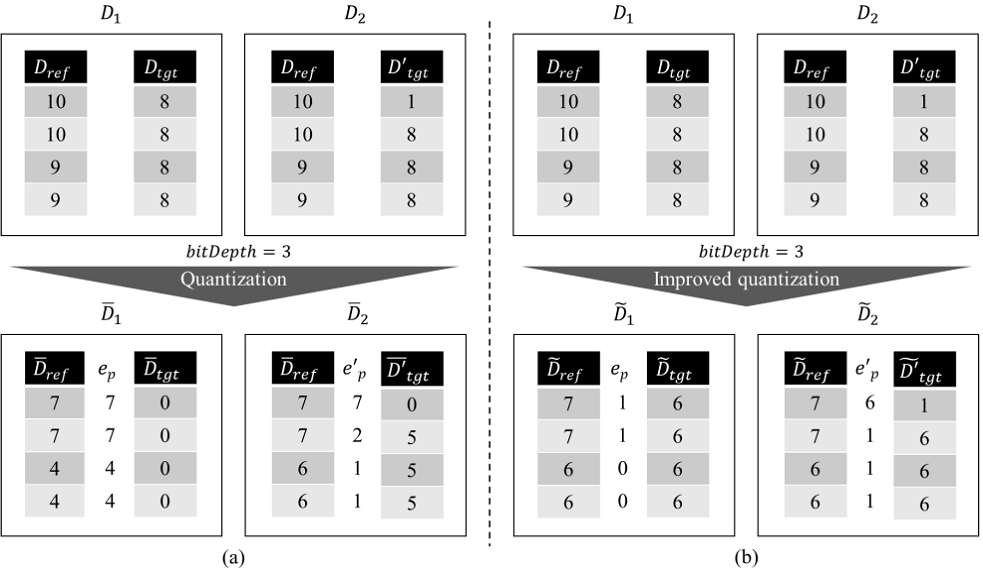
는 와 의 합집합, 는 의 최댓값, 은 개선된 양자화를 통해 정수로 변환된 밀도 값이다. 일반적으로, 최솟값을 이용한 양자화는 0 보다 작은 음수 값을 양수로 변환하면서도 값의 분포도를 유지한 채로 ‘0 ~ 2bitDepth-1’의 범위를 갖는 정수 값을 생성할 수 있어, 다양한 분야에서 널리 활용되는 방법이다. 하지만, 밀도 값은 0 미만의 값을 가질 수 없으며, 밀도 집합(D)의 최솟값은 대상 포인트 클라우드의 밀도 왜곡 정도에 따라 최솟값이 크게 변경된다. 따라서, 양자화에 최솟값을 사용하게 되면, 양자화된 정수 값에 대응되는 밀도 값이 최솟값에 따라 변하게 되고, 서로 다른 대상 포인트 클라우드의 밀도 품질의 비교를 어렵게 만든다. 본 논문에서 제안하는 ‘개선된 양자화’ 기술은 수식 (8)과 같이, 최솟값을 양자화에서 사용하지 않으며, 제안 기술의 효용성은 그림 9의 예시를 통해 확인할 수 있다.
그림 9-(a)의 D1과 같이, Dref가 최대 10의 밀도를 갖고 있고, Dtgt에서는 밀도가 손실되어 최소 8의 밀도를 가질 때, D3-PSNR의 양자화 bitDepth가 3인 경우, 8에서 10까지의 값을 ‘0 ~ 7’ 범위의 값으로 변환한다. 만일 그림 9-(a)의 D2와 같이, 동일한 Dref를 기준으로 최소 1의 밀도를 갖는 D'tgt를 상정하면, D3-PSNR의 양자화는 1에서 10까지의 값을 ‘0 ~ 7’ 범위의 값으로 변환한다. 전자의 경우 밀도 상에서 ‘1’만큼 일어난 손실은 양자화된 정수 값에서 ‘4’로 표현되고, 후자의 경우 ‘1’로 표현된다. 따라서, 실제로는 더 적게 손실된 D1 밀도 오류 값(ep)이 D2의 오류 값(e'p)보다 더 커지게 된다. 그림 9-(b)는 그림 9-(a)와 동일한 조건에서 본 논문에서 제안하는 ‘개선된 양자화’ 기술을 사용하였을 경우의 결과를 보여주고 있으며, D1과 D2의 밀도 손실 경향과 ep와 e'p의 경향이 일치하는 것을 확인할 수 있다.
‘개선된 양자화’를 통해 획득한 참조 및 대상 포인트 클라우드의 밀도(, ) 값들은 그림 8의 오류 계산(Error calculation) 단계를 통해 오류 값으로 변환된다. 오류 값 변환은 D3-PSNR의 수식 (2)와 동일하게 수행되며, 이후 그림 2의 D3-PSNR 계산(D3-PSNR calculation) 모듈과 동일한 과정을 거쳐 PSNR으로 도출된다.
본 논문은 기존의 밀도 품질 평가의 한계를 극복하기 위해 표면 추정 및 이상치 제거 기반의 포인트 클라우드 밀도 품질 평가 고도화 방안을 제안하였다. 제안 기술은 단위 반경, 이상치, 양자화 등의 측면에서 기존 D3-PSNR과 ‘밀도 적응적 왜곡 결정’ 방식의 한계를 확인하고, 이를 해결하기 위해 ‘표면 추정 기반 밀도 계산 고도화’ 방안과 ‘이상치 제거 및 개선된 양자화 기반 오류 결정 고도화’ 방안을 제시하였다. 제시된 방안들의 검증을 위해 Ⅳ장에서는 본 논문의 실험 환경과 실험 결과를 확인한다.
Ⅳ. 실험 환경 및 결과
본 논문의 표면 추정 및 이상치 제거 기반의 포인트 클라우드 밀도 품질 평가 고도화 방안은 참조 포인트 클라우드의 특성에 따라 대상 포인트 클라우드의 밀도 왜곡을 보다 정확하게 수치화 하고, 평가 값을 객관적으로 비교하기 위해 제안되었다. 이를 검증하기 위해, 본 논문의 실험은 3DGH G-PCC(Geometry-based Point Cloud Compression)의 CTC(Common Test Condition)[5]에서 정의된 포인트 클라우드 테스트 데이터 세트를 기반으로 수행되었으며, 밀도 왜곡 생성에는 G-PCC의 참조 소프트웨어 버전 20(Reference software v20.0)[18]과 AI-PCC의 GRASP-net[19]을 사용하였다. 본 논문의 실험에 사용된 테스트 데이터 세트의 세부 사항은 표 1과 같다.
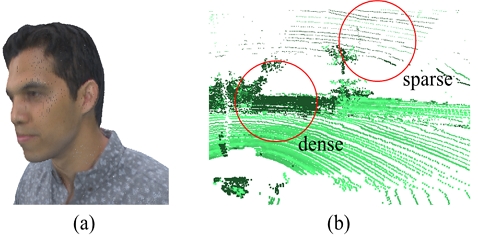
표 1의 프레임 번호(Frame number)는 각 데이터 세트 중 실험에 사용된 프레임의 번호를 나타내며, 유형(Type)은 테스트 데이터 세트 내 포인트 클라우드들을 밀도 특성에 따라 고밀도(Dense) 또는 복합(Hybrid)으로 분류한 것이며, 전체 밀도(Whole density) 값은 포인트 클라우드 내 전체 점들이 점유하고 있는 공간의 크기 대비 전체 점 개수의 값을 나타낸 것이다. 유형(Type) 별 포인트 클라우드의 밀도 특성은 그림 10에서 확인할 수 있다.
고밀도 유형의 포인트 클라우드는 그림 10-(a)와 같이, 포인트 클라우드 내 점들이 치밀하게 표면을 형성하고 있으며, 복합 유형의 포인트 클라우드는 그림 10-(b)와 같이, 저밀도(Sparse) 영역과 고밀도(Dense) 영역이 복합적으로 존재하는 것이 확인된다. 이처럼, 두 종류의 포인트 클라우드 데이터가 서로 상이한 밀도 특성을 나타내므로 본 논문의 실험에서는 각 데이터 유형에 따라 서로 다른 조건으로 밀도 왜곡 평가를 수행하며, 이에 대한 세부 사항은 Ⅳ장의 각 절에서 상세히 설명된다.
1. 표면 추정 기반 밀도 계산 고도화 방안의 검증
‘표면 추정 기반 밀도 계산 고도화’ 방안은 사전 설정된 KNN 값과 유사한 점의 개수를 탐색할 수 있는 단위 반경을 구하기 위해 제안되었다. 추정된 단위 반경의 검증은 PCref의 각 점을 기준으로 계산된 을 모두 더한 뒤 PCref의 점 개수로 나눈 평균 값을 사전 설정된 KNN 값과 비교하여 검증된다. 테스트 데이터 세트를 기반으로 D3-PSNR과 제안 기술에서 각각 획득된 평균 값은 표 2와 같다.
표 2의 결과는 D3-PNSR과 D3-PSNR에 ‘표면 추정 기반 밀도 계산 고도화’ 방안만을 적용하여 획득된 것이며, 평균 값을 각 테스트 데이터 별로 나타내고 있다. 이때, KNN 값은 64와 128로 설정하여 실험되었으며, 파티션 분할 계수(Cpart)는 32와 64를 사용하였다. 따라서, D3-PSNR과 제안 기술은 테스트 데이터 별로 각각 4가지의 평균 값을 갖게 된다. 표 2의 녹색으로 표시된 영역에서 확인되는 바와 같이, 제안 기술은 모든 고밀도 유형의 데이터에서 D3-PSNR에 비해 사전 정의된 KNN과 유사한 평균 값을 획득함을 알 수 있다. 제안된 ‘표면 추정 기반 밀도 계산 고도화’ 방안은 포인트 클라우드의 표면을 곡면으로 가정하고 있으므로, 곡면을 가장 뚜렷하게 나타내는 고밀도 유형의 데이터에서 KNN과 가장 유사한 평균 값을 도출하는 것이다. 하지만, 포인트 클라우드의 표면이 곡면을 구성하지 않는 복합 유형의 데이터에서는 D3-PSNR과 제안기술 사이에 유의미한 차이를 발견하기 어렵다. 따라서, 제안된 ‘표면 추정 기반 밀도 계산 고도화’ 방안은 곡면을 이루는 고밀도 유형의 포인트 클라우드에서 D3-PSNR에 비해 정확한 단위 반경을 추정함을 알 수 있다.
2. 이상치 제거 및 개선된 양자화 기반 오류 결정 고도화 방안의 검증
본 논문에서 제안된 ‘이상치 제거 및 개선된 양자화 기반 오류 결정 고도화’ 방안은 ‘이상치 제거’와 ‘개선된 양자화’ 기술을 통해 기존 기술의 한계점을 극복한다. 본 논문에서 제안하는 ‘이상치 제거’ 기술은 ‘밀도 적응적 왜곡 결정’ 방식에서 초저밀도의 영향을 줄이기 위한 목적으로 개발되었으며, ‘개선된 양자화’ 기술은 동일 참조 포인트 클라우드에서 발생한 밀도 왜곡을 갖는 대상 포인트 클라우드들을 공정하게 비교하기 위해 제안되었다. ‘밀도 적응적 왜곡 결정’ 방식은 복합 유형의 데이터를 대상으로 제안된 기술이므로, ‘이상치 제거’ 기술의 검증은 복합 유형 데이터를 대상으로 수행되며, ‘개선된 양자화’ 기술은 테스트 세트 전체를 대상으로 검증된다. 복합 유형 데이터에서 ‘표면 추정 기반 밀도 계산 고도화’ 기술은 표 2에서 확인된 바와 같이 D3-PSNR의 단위 반경 추정 방식의 결과와 큰 차이가 없다는 것이 확인되었다. 따라서, 복합 유형 데이터의 실험에서 단위 반경은 D3-PSNR의 단위 반경 추정으로 획득하여 ‘이상치 제거’ 기술과 ‘개선된 양자화’ 기술의 성능을 보다 정밀하게 검증한다. 검증 조건은 평균 값이 너무 크지 않은 ‘KNN: 64, Cpart: 64’ 조건을 사용하여 수행되었다. 고밀도 유형 데이터의 실험은 D3-PNSR의 기본 값인 ‘KNN: 64, Cpart: 32’ 조건을 사용하여 수행되었다.
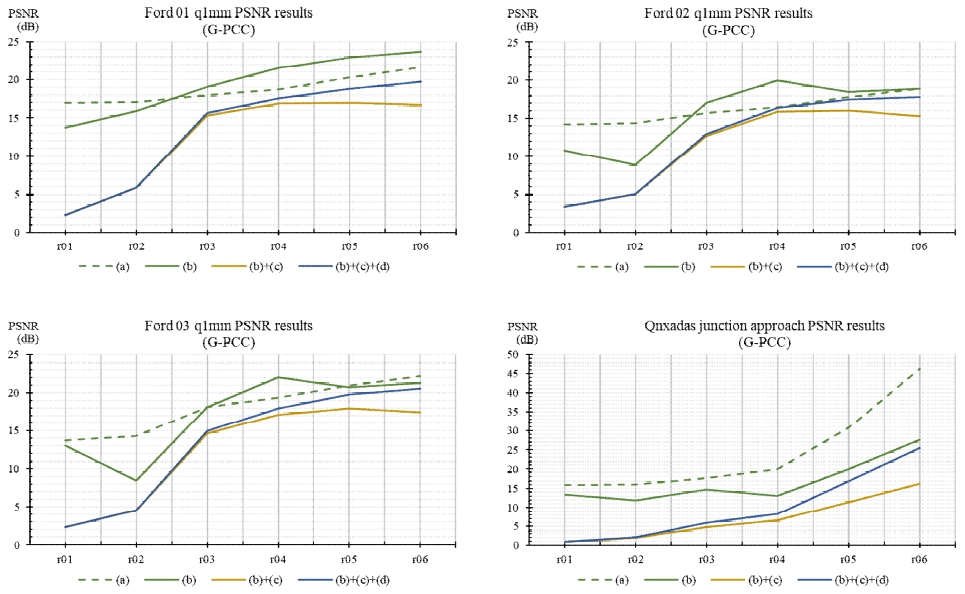
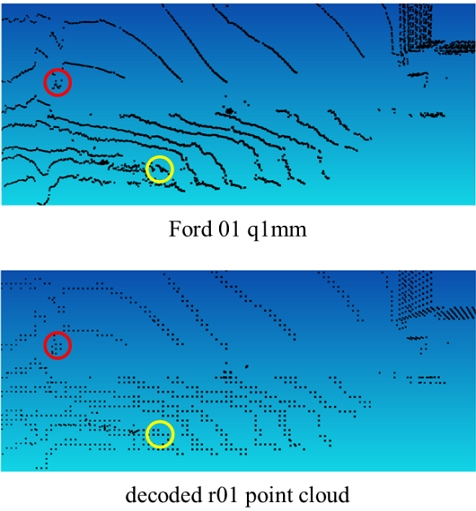
그림 11은 G-PCC를 통해 부·복호화된 복합 유형 데이터의 밀도 왜곡 평가 결과를 나타낸다. 가로축의 양자화 단계(r01~r06)는 G-PCC의 CTC[5]에 정의된 값을 사용하였으며, 세로축은 밀도 왜곡 평가를 통해 도출된 PSNR 값을 나타낸다. 그림 11에서 (a)는 D3-PSNR, (b)는 ‘밀도 적응적 왜곡 결정’ 기술, (c)는 ‘이상치 제거’ 기술(이상치 문턱 값, Oth=10), (d)는 ‘개선된 양자화’ 기술을 의미한다. 실험은 (b)에 제안 기술인 (c)와 (d)를 적용 시 발생하는 밀도 왜곡 평가 수치의 변동을 확인할 수 있도록 설계되었다. 그림 11의 결과에서 확인되는 바와 같이, 실험 (b)+(c)에서는 낮은 비트레이트에서 PSNR이 급격히 떨어지는 것을 확인할 수 있다. 이는 밀도 왜곡 평가 값에서 Oth 이하의 점 개수를 갖는 영역이 큰 부분을 차지하고 있었음을 의미하며, 낮은 비트레이트 조건에서 G-PCC는 초저밀도 영역을 타 영역에 비해 적게 손실 시킨다는 것을 알 수 있다. 실험 (b)+(c)+(d)에서는 낮은 비트레이트의 경향은 유지된 채 높은 비트레이트의 PSNR이 상승하는 것을 확인할 수 있다. 이는 Ⅲ-2절의 그림 9에서 확인된 바와 같이, ‘개선된 양자화’ 기술(d)이 밀도 오류 값이 밀도 손실의 경향성을 따르도록 유도하였기 때문이다. 앞서 PSNR 값을 통해 확인된 밀도 왜곡 평과 결과는 실제 포인트 클라우드의 손실 정도와 밀도 오류 맵을 비교하는 것으로 보다 더 분명하게 검증할 수 있다. 이를 위해 본 논문은 그림 12에서 보여지는 원본 포인트 클라우드 데이터와 복원된 포인트 클라우드의 결과를 비교하여 G-PCC의 손실 특성을 확인하고, 그림 13의 밀도 오류 맵을 통해 각 실험의 영향을 보다 자세하게 확인한다.
그림 12의 상단은 Ford 01 q1mm의 원본 포인트 클라우드, 하단은 r01 조건으로 압축 후 복원된 포인트 클라우드, 빨간색 원은 저밀도 영역, 노란색 원은 고밀도 영역을 나타낸다. 빨간색 원의 저밀도 영역은 점의 손실이 적으나, 상대적으로 고밀도 영역인 노란색 원은 많은 수의 점이 손실된 것을 확인할 수 있다. 따라서, 고밀도 영역에서 높은 에러 값이, 저밀도 영역에서는 낮은 에러 값이 도출되도록 평가하는 방법이 실제 점의 손실 정도를 더 잘 반영하는 기술임을 알 수 있다.
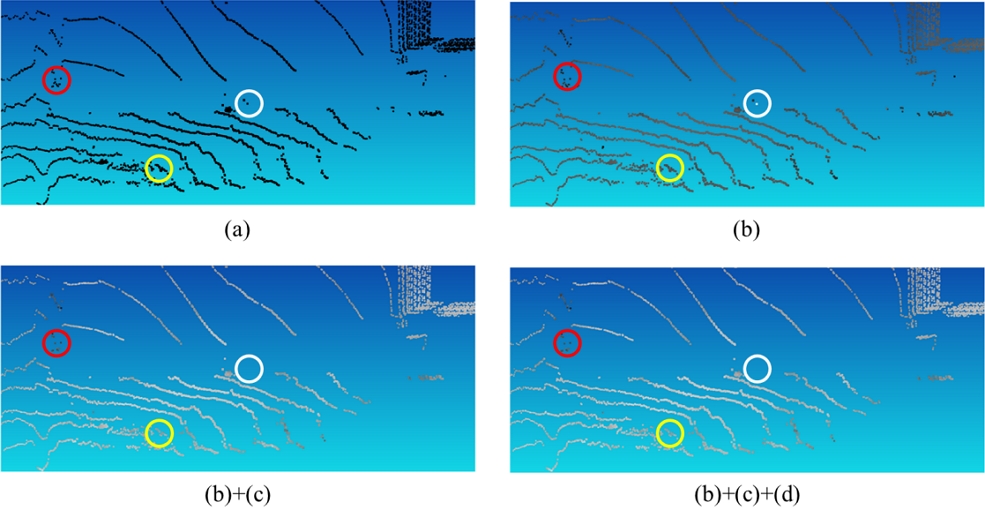
그림 13의 실험들은 그림 11과 동일하게 (a)는 D3-PSNR, (b)는 ‘밀도 적응적 왜곡 결정’ 기술, (c)는 ‘이상치 제거’ 기술(이상치 문턱 값, Oth=10), (d)는 ‘개선된 양자화’ 기술을 의미하며, 밀도 오류 맵은 밀도 오류 값을 0~255의 값으로 변환하여 오류가 커질수록 흰색에 가깝도록 표현되었다. 그림 13의 빨간색 원과 노란색 원에서 보이는 바와 같이, (b)는 (a)에 비해 저밀도 영역은 약간 어둡게, 고밀도 영역은 밝게 나타나므로 G-PCC 손실 압축에서 나타나는 밀도 오류를 보다 더 정확하게 표현하는 것으로 보인다. 하지만, 흰색 원과 같이 초저밀도에서 이상치 값이 존재하는 것을 확인할 수 있다. 본 논문의 제안 기술을 이용한 실험인 (b)+(c)와 (b)+(c)+(d)의 경우, (a)와 (b)에 비해 저밀도 영역과 고밀도 영역에서 나타나는 오류 값의 차이가 두드러지는 것을 확인할 수 있으며, (b)에서 발생하던 이상치 값이 (b)+(c)와 (b)+(c)+(d)에서는 사라진 것이 확인된다.
그림 14는 GRASP-net을 통해 부·복호화된 복합 유형 데이터의 밀도 왜곡 평가 결과를 나타내며, 가로축의 양자화 단계(r01~r05)는 GRASP-net[19]에서 정의된 값을 사용하였다. 또한, 각 실험에 사용된 조건과 기술은 그림 11의 실험과 동일하다. 결과에서 확인되는 바와 같이, 실험 (b)+(c)에서 낮은 비트레이트의 PSNR이 급격하게 떨어지는 것을 알 수 있다. 또한, 실험 (b)의 결과와 달리, 실험 (b)+(c)의 결과는 하강 곡선에서 상승 후 하강 곡선으로 변경되는데, 이는 GRASP-net의 복호화된 포인트 클라우드의 밀도 특성과 동일하며, 표 3에서 보다 자세히 확인할 수 있다.
표 3에서 보이는 바와 같이, GRASP-net을 통해 복호화된 복합 유형 포인트 클라우드는 r02 혹은 r03 양자화 단계를 기점으로 원본 포인트 클라우드의 점 개수보다 많은 수의 점을 갖게 된다. 이에, r02 혹은 r03 양자화 단계에서 가장 높은 PSNR 값이 도출된 뒤, 그 이후의 양자화 단계부터는 대상 포인트 클라우드의 밀도 상승으로 인한 밀도 왜곡이 발생하여 PSNR 값이 낮아질 것을 예상할 수 있다. 그림 14에서 보이는 바와 같이, 실험 (a)와 (b)의 결과에서는 GRASP-net의 밀도 왜곡 특성이 두드러지지 않으나, 실험 (b)+(c)의 결과는 GRASP-net의 밀도 왜곡 특성을 보다 더 명확하게 반영하고 있다. 또한, 실험 (b)+(c)+(d)에서는 낮은 비트레이트의 경향은 유지된 채 높은 비트레이트의 PSNR이 약간 상승하는 것을 확인할 수 있다.
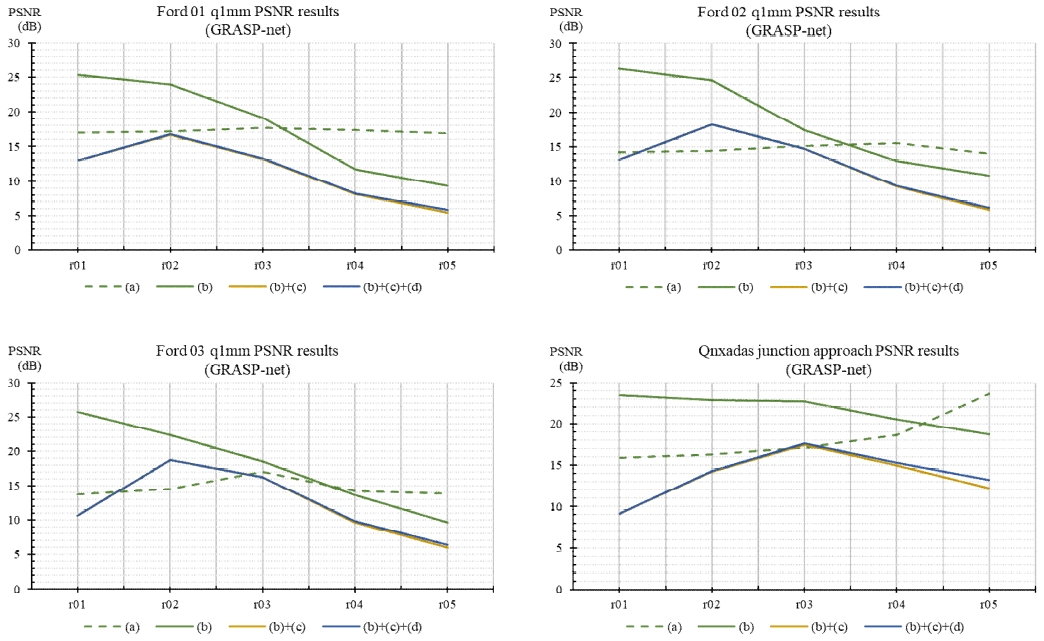
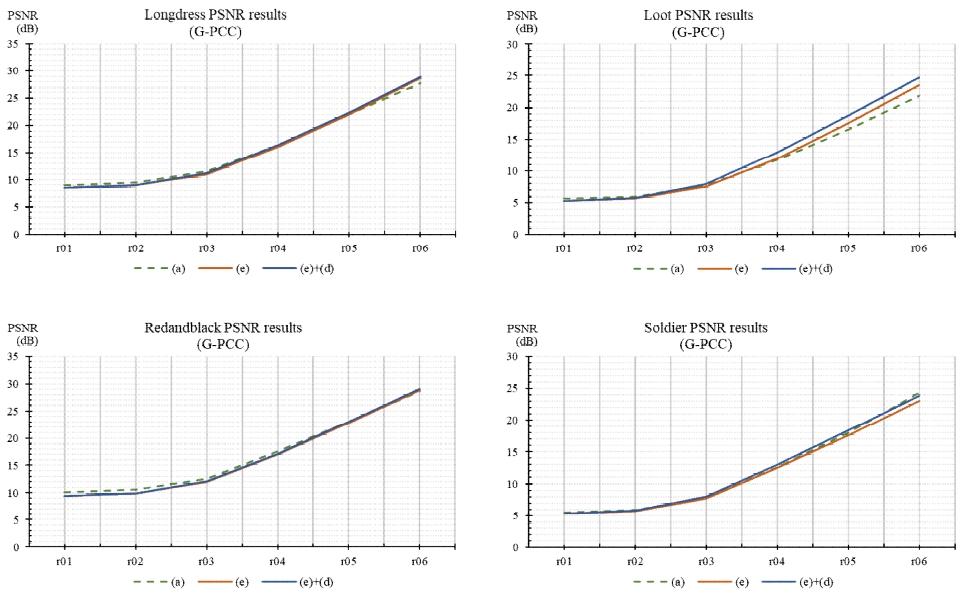
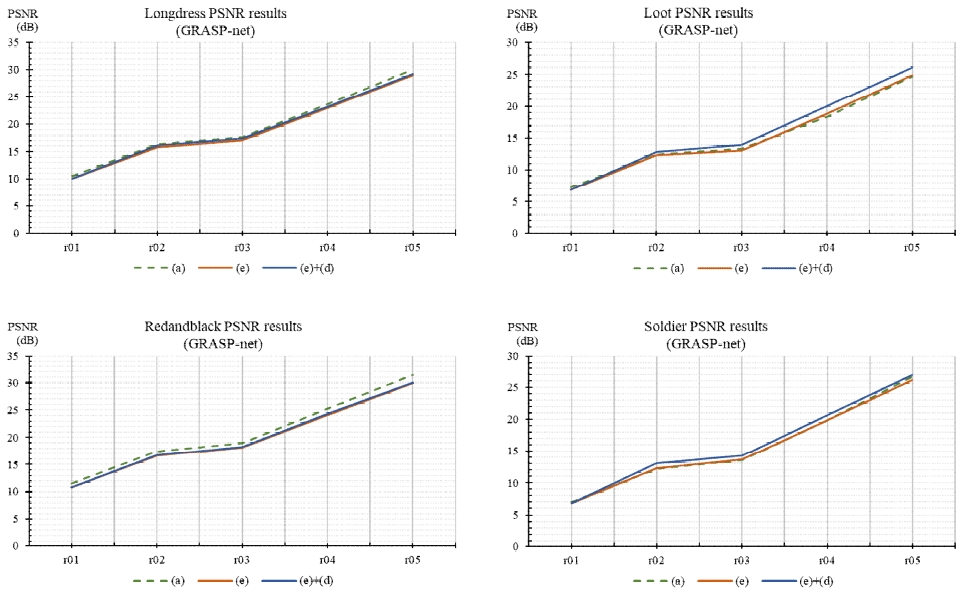
그림 15는 G-PCC를 통해 부·복호화된 고밀도 유형 데이터의 밀도 왜곡 평가 결과를 나타내며, 가로축과 세로축은 그림 11과 동일하다. 그림 15에서 (a)는 D3-PSNR, (e)는 ‘표면 추정 기반 밀도 계산 고도화’ 기술, (d)는 ‘개선된 양자화’ 기술을 의미한다. 실험은 (a)에 제안 기술인 (e)와 (d)를 적용 시 발생하는 밀도 왜곡 평가 수치의 변동을 확인할 수 있도록 설계되었다. 그림 15에서 확인되는 바와 같이, 실험 (e)는 기존 D3-PSNR의 결과 값과 거의 동일한 값을 갖는다. 이는 고밀도 유형의 경우, 포인트 클라우드의 부분영역들이 균일한 밀도를 갖고, G-PCC가 부분영역들의 밀도를 동일하게 떨어뜨리기 때문이다. 이로 인해 단위 반경에 따라 부분영역의 크기가 달라져도 밀도 왜곡 결과의 차이가 적게 나타나게 된다. 따라서, 표 2에서 확인된 바와 같이, ‘KNN: 64, Cpart: 32’ 조건에서 D3-PSNR의 평균 값은 115.8이며, (e)는 58.4이므로 탐색되는 점의 개수 차이가 약 2배인 단위 반경으로 밀도를 비교하였음에도 불구하고, 유사한 밀도 왜곡 값이 도출되는 것이다. 실험 (e)+(d) 또한 복합 유형 데이터의 결과와는 달리 기존 D3-PSNR과 큰 차이가 나타나지 않는데, 이는 각 부분영역에서 발생한 밀도 왜곡의 정도가 유사하여 단일 대상 포인트 클라우드 내에 최솟값의 수치도 유사하게 되고, 이로 인해 ‘개선된 양자화’ 기술의 효과가 적기 때문이다.
그림 16은 GRASP-net을 통해 부·복호화된 고밀도 유형 데이터의 밀도 왜곡 평가 결과를 나타내며, 가로축과 세로축, 그리고 각 실험에 사용된 조건과 기술은 그림 15의 실험과 동일하다. 표 3에서 확인된 바와 같이, 복합 유형 데이터의 결과와는 달리 GRASP-net의 고밀도 유형 데이터 결과는 원본 데이터의 밀도와 점진적으로 유사해진다. 그림 16의 결과 또한 동일한 추세를 보이며, 그림 15에서 확인된 바와 동일한 원인으로 실험 (a), 실험 (e), 실험 (e)+(d)는 유사한 값을 갖는다.
본 장의 1절에서는 제안된 ‘표면 추정 기반 밀도 계산 고도화’ 방안을 사전 정의된 KNN과 평균 값을 비교하여 검증하였으며, 2절에서는 ‘이상치 제거 및 개선된 양자화 기반 오류 결정 고도화’ 방안의 밀도 왜곡 평가 결과를 코덱의 압축 왜곡과 비교하여 검증하였다. 또한, ‘표면 추정 기반 밀도 계산 고도화’ 방안의 밀도 왜곡 평가 결과를 제시하여 고밀도 유형 데이터에서 제안 기술과 기존 기술들의 평가 결과를 비교하였다. 이를 통해, 제안 기술의 밀도 평가 결과는 복합 유형 데이터에서의 기존 밀도 왜곡 평가 기술들의 한계점을 극복하고, 코덱 손실 압축의 밀도 왜곡 특성과 유사한 밀도 왜곡 평가 결과를 나타냄이 확인되었다. 고밀도 유형 데이터 측면에서는 밀도 왜곡 평가 시, 입력 조건(KNN)과 결과( 평균 값)가 일치할 수 있도록 지원하여 밀도 왜곡 평가 결과의 신뢰도를 개선할 수 있음이 확인되었다. 따라서, 제안된 ‘표면 추정 및 이상치 제거 기반 포인트 클라우드 밀도 품질 평가 방안’은 다양한 유형의 포인트 클라우드의 밀도 왜곡을 보다 정확하게 평가할 수 있다.
Ⅴ. 결 론
포인트 클라우드의 밀도 왜곡을 정량적으로 평가하기 위하여 원본 포인트 클라우드와 복호화된 포인트 클라우드 사이에서 각 점의 밀도를 비교하는 밀도 품질 평가 방안인 D3-PSNR과 ‘밀도 적응적 왜곡 결정’ 방식이 제안되었다. 하지만, D3-PSNR과 ‘밀도 적응적 왜곡 결정’ 방식은 각각 서로 다른 한계점이 존재한다. 제안 기술은 D3-PSNR의 단위 반경 정확도 문제를 해결하기 위해 ‘표면 추정 기반 밀도 계산 고도화’ 방안을 제안하였으며, ‘밀도 적응적 왜곡 결정’ 방식에서 나타나는 초저밀도의 영향을 줄이기 위해 ‘이상치 제거 및 개선된 양자화 기반 오류 결정 고도화’ 방안을 제시하였다. Ⅳ장의 실험 결과에서 검증된 바와 같이, ‘표면 추정 기반 밀도 계산 고도화’ 방안은 고밀도 유형의 포인트 클라우드에서 D3-PSNR에 비해 보다 더 정확한 단위 반경을 도출한다는 것이 확인되었으며, ‘이상치 제거 및 개선된 양자화 기반 오류 결정 고도화’ 방안은 포인트 클라우드 코덱들의 압축 손실 특성을 ‘밀도 적응적 왜곡 결정’ 방식에 비해 보다 더 명확하게 나타내는 것이 확인되었다.
Acknowledgments
This research was supported by the MSIT(Ministry of Science and ICT), Korea, under the ITRC(Information Technology Research Center) support program (Grant number: IITP-2023-2021-0-02046) and (No. RS-2023-00227431, Development of 3D space digital media standard technology) supervised by the Institute of Information & communications Technology Planning & evaluation (IITP).
References
-
Y. Hwang, J. Kim and K. Kim, “2D Interpolation of 3D Points using Video-based Point Cloud Compression,” JOURNAL OF BROADCAST ENGINEERING, 26(6), 692-703. Nov. 2021.
[https://doi.org/10.5909/JBE.2021.26.6.692]

-
H. Liu, H. Yuan, Q. Liu, J. Hou and J. Liu, "A Comprehensive Study and Comparison of Core Technologies for MPEG 3-D Point Cloud Compression," in IEEE Transactions on Broadcasting, vol. 66, no. 3, pp. 701-717, Sept. 2020.
[https://doi.org/10.1109/TBC.2019.2957652]

-
K. Nam, J. Kim, M. Han, K. Kim and M. Hwang, “Comparative Experiment of 2D and 3D DCT Point Cloud Compression,” JOURNAL OF BROADCAST ENGINEERING, 26(5), 553-565. Sep. 2021.
[https://doi.org/10.5909/JBE.2021.26.5.553]

-
L. Li, Z. Li, S. Liu and H. Li, "Rate Control for Video-Based Point Cloud Compression," in IEEE Transactions on Image Processing, vol. 29, pp. 6237-6250, 2020.
[https://doi.org/10.1109/TIP.2020.2989576]

- "Common Test Conditions for G-PCC," ISO/IEC JTC1/SC29/WG7, N578, Apr. 2023.
-
J. Im, J. Kim, S. Rhyu and K. Kim, "A method of level of details control table for 3D point density scalability in video based point cloud compression," Proc. SPIE 11137, Applications of Digital Image Processing XLII, 111371A, Sep. 2019.
[https://doi.org/10.1117/12.2527314]

- A. Zaghetto, D. Graziosi and A. Tabatabai, "Density Distortion Metric," ISO/IEC JTC1/SC29/WG7, M60331, Jul. 2022.
- J. Kim, M. Lee and K. Kim, "Adaptive Density-based Point Cloud Evaluation Technology using Sparsity Ratios," The Korean Institute of Broadcast and Media Engineers Summer Conference, Jun. 2023.
- "On AI Tools for Point Cloud Compression and Analysis," ISO/IEC JTC1/SC29/WG7, N652, Jul. 2023.
-
J. Wang, D. Ding, Z. Li and Z. Ma, "Multiscale Point Cloud Geometry Compression," 2021 Data Compression Conference, Snowbird, UT, USA, pp. 73-82, 2021.
[https://doi.org/10.1109/DCC50243.2021.00015]

-
J. Pang, M. A. Lodhi, and D. Tian, "GRASP-Net: Geometric Residual Analysis and Synthesis for Point Cloud Compression," In Proceedings of the 1st International Workshop on Advances in Point Cloud Compression, Processing and Analysis, pp.11–19, 2022.
[https://doi.org/10.1145/3552457.3555727]

-
M. Quach, G. Valenzise and F. Dufaux, "Learning Convolutional Transforms for Lossy Point Cloud Geometry Compression," IEEE International Conference on Image Processing(ICIP’2019), Taipei, Taiwan, Sep. 2019. pp.4320-4324,
[https://doi.org/10.1109/ICIP.2019.8803413]

-
J. Wang, H. Zhu, H. Liu and Z. Ma, "Lossy Point Cloud Geometry Compression via End-to-End Learning," in IEEE Transactions on Circuits and Systems for Video Technology, vol. 31, no. 12, pp. 4909-4923, Dec. 2021.
[https://doi.org/10.1109/TCSVT.2021.3051377]

- A. Zaghetto, D. Graziosi and A. Tabatabai, "Density-to-density (D3-PSNR) Script Availability," ISO/IEC JTC1/SC29/WG7, M61195, Oct. 2022.
-
J. L. Bentley, ‘‘Multidimensional binary search trees used for associative searching,’’ Commun. ACM, vol. 18, no. 9, pp. 509–517, 1975.
[https://doi.org/10.1145/361002.361007]

- M. Lee, J. Kim, K. Park, K. Kim, J. Lee and S. Jung, "Density Distortion Metric," ISO/IEC JTC1/SC29/WG7, M62966, Apr. 2023.
- J. Stewart, Calculus Early Transcendentals, Thomson Higher Education, Belmont USA, 2008.
- Point Cloud Compression Test Model Category 13 Reference Software Release-v20.0, http://mpegx.int-evry.fr/software/MPEG/PCC/TM/mpeg-pcc-tmc13/-/tree/release-v20.0, (accessed Sep. 24, 2023)
- GRASP-Net: Geometric Residual Analysis and Synthesis for Point Cloud Compression, https://github.com/InterDigitalInc/GRASP-Net, (accessed Sep. 24, 2023)

- 2017년 2월 : 경희대학교 전자·전파공학과 공학사
- 2019년 2월 : 경희대학교 전자공학과 공학석사
- 2022년 8월 : 경희대학교 전자정보융합공학과 공학박사
- 2022년 5월 ~ 현재 : 한국정보통신기술협회 소프트웨어시험인증연구소 선임연구원
- ORCID : https://orcid.org/0000-0002-0287-9640
- 주관심분야 : 멀티미디어 시스템, 포인트 클라우드 압축, 디지털 대화형 방송

- 2021년 8월 : 경희대학교 전자공학과 공학사, 컴퓨터공학과 공학사
- 2021년 9월 ~ 현재 : 경희대학교 전자정보융합공학과 석사과정
- ORCID : https://orcid.org/0000-0001-6500-7156
- 주관심분야 : 딥러닝모델 경량화, 영상처리, 멀티미디어 시스템

- 1989년 2월 : 한양대학교 전자공학과 공학사
- 1992년 9월 : 영국 University of Newcastle upon Tyne 전기전자공학과 공학석사
- 1996년 7월 : 영국 University of Newcastle upon Tyne 전기전자공학과 공학박사
- 1996년 ~ 1997년 : 영국 University of Sheffield, Research Fellow
- 1997년 ~ 2006년 : 한국전자통신연구원 대화형미디어연구팀장
- 2006년 ~ 현재 : 경희대학교 전자정보대학 교수
- ORCID : http://orcid.org/0000-0003-1553-936X
- 주관심분야 : 영상처리, 멀티미디어통신, 디지털 대화형방송