심층신경망 기반의 프리코딩 시스템을 활용한 다중사용자 스케줄링 기법에 관한 연구

Ⅰ. 서 론

다중사용자 다중안테나(MU-MIMO) 환경에서는 복수의 안테나를 통한 신호의 다중화(multiplexing)이 가능하기 때문에 같은 시간-주파수 자원내에서 전송가능한 데이터율을 증가시킬 수 있다. 하지만 MU-MIMO 환경에서 효과적인 신호의 다중화를 수행하기 위해서는 송신부가 비교적 정확한 채널의 정보를 알아야 하며, 기존의 통신시스템에서는 제한된 피드백을 통해 이 문제를 주로 해결하였다^[1]. 하향링크를 예로 들면, 각 사용자는 자신의 채널을 추정하고, 추정된 채널을 사전에 정해진 코드북을 통해 양자화하여 송신부에 피드백하고, 송신부는 피드백 받은 정보를 활용하여 적절한 프리코딩을 통해 신호를 다중화한다. 이러한 시스템의 전체 과정을 한번에 통합하여 최적화하는 것은 어렵기 때문에 기존의 시스템은 채널 추정, 채널 양자화, 피드백, 프리 코딩 등의 과정을 개별적으로 최적화하여 사용해 왔다.

최근의 연구에서는 deep learning (DL)을 기반으로 상기한 과정들을 일괄적으로 포괄하여 최적화하는 방식이 제안된 바 있다^[2]. 해당 시스템은 송수신부에 이와 같은 과정을 내포하는 심층신경망(DNN)을 각각 활용하며, DNN들은 시스템의 sum rate가 최대화 되도록 오프라인 학습을 통해 스스로를 최적화하며, 그 결과 기존의 시스템에 비해, 특히 피드백 정확도가 떨어지는 환경에서, 높은 잠재력을 가짐이 실험을 통해 확인되었다. 하지만 해당 연구는 미리 준비된 동등한 사용자를 대상으로 프리코딩을 수행하고 있기 때문에, 실제 환경과 같이 많은 사용자들 중 상황에 적합한 사용자를 스케줄링 하는 경우에는 그대로 적용하기 어렵다. 해당 시스템을 많은 사용자가 존재하는 상황에 그대로 적용하려면 학습이 필요한 전체 네트워크의 사이즈가 지나치게 비대해져서 실용성이 떨어지기 때문이다. 따라서 본 연구에서는 기존에 제안된 DNN 기반의 프리코딩기법을 활용한 실용적인 사용자 스케줄링 기법을 제안하고자 하며, 해당 기법이 기존의 코드북 기반의 기법에 비해 얼마나 높은 잠재력을 가지는지 확인해보고자 한다.

Ⅱ. 시스템 모델

하나의 기지국이 M개의 송신안테나를 통해 K명의 유저와 동시에 통신하는 시스템을 고려한다. 각 유저는 1개의 수신 안테나를 가지며, 따라서 각 유저의 수신신호는

로 주어지고, 여기서 h_k는 유저 k와 기지국 사이의 채널 행렬이며, 각 원소가 독립적인 평균 0, 분산 1의 complex Gaussian분포를 가진다. n_k는 평균 0, 분산 1을 가지는 complex additive Gaussian 잡음이다. 송신 벡터 x는 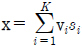로 주어진다. v_i는 각 사용자를 위한 프리코딩 벡터이며, s_i는 유저 i를 위해 준비된 송신 신호이다. 송신 파워는 E{ x∥²}=P로 제한되고, 각 유저에게 동일하게 분배된다. 각 유저는 자신의 채널을 2^B사이즈의 코드북을 통해 양자화하여 피드백한다. 본 논문에서는 [2]에서 제안된 DNN 기반의 프리코딩을 활용해 각 사용자가 B비트의 implicit한 피드백을 송신부로 보내는 방식을 사용한다.

Ⅲ. 다수의 사용자가 존재하는 상황에서 적합한 스케줄링 기법

본 절에서는 [2]에서 제안된 DNN-기반의 프리코딩구조를 활용하여 효율적으로 잠재력이 높은 사용자를 선택하는 기법을 제안한다. 통상적으로 송신 안테나 수보다 많은 수의 사용자가 존재하는 환경에서는 기대치가 높은 사용자의 조합을 송신 안테나의 수만큼 스케줄링한 후에 프리코딩을 진행하며, MU-MIMO 시스템의 구성은 순서대로 채널의 양자화, 피드백, 스케줄링, 프리코딩의 순서로 모듈화하여 동작한다. 이러한 모든 과정을 지도학습을 통해 동시에 학습하는 것이 최적의 방법이지만 사용자 수가 많은 환경에서는 복잡도 등의 이슈로 인해 실현가능성이 굉장히 낮다. 스케줄링이 없는 상황이라면 기존의 연구^[2]에서 보여주듯이 전체 과정을 학습하는 것이 가능하다. 게다가 이러한 과정은 주어진 송신 안테나의 수로 크기가 정해지는 MIMO 채널의 정보를 주어진 DNN을 사용하여 압축하는 것과 유사하게 해석할 수 있다. 이러한 관점에서 주어진 MU-MIMO 채널의 정보를 적절하게 압축하는 과정은 기존의 연구 결과^[2]와 동일하게 진행하고, 이러한 압출결과에 적합한 새로운 스케줄링 기법을 제안하는 것이 본 연구의 핵심 목표이다.

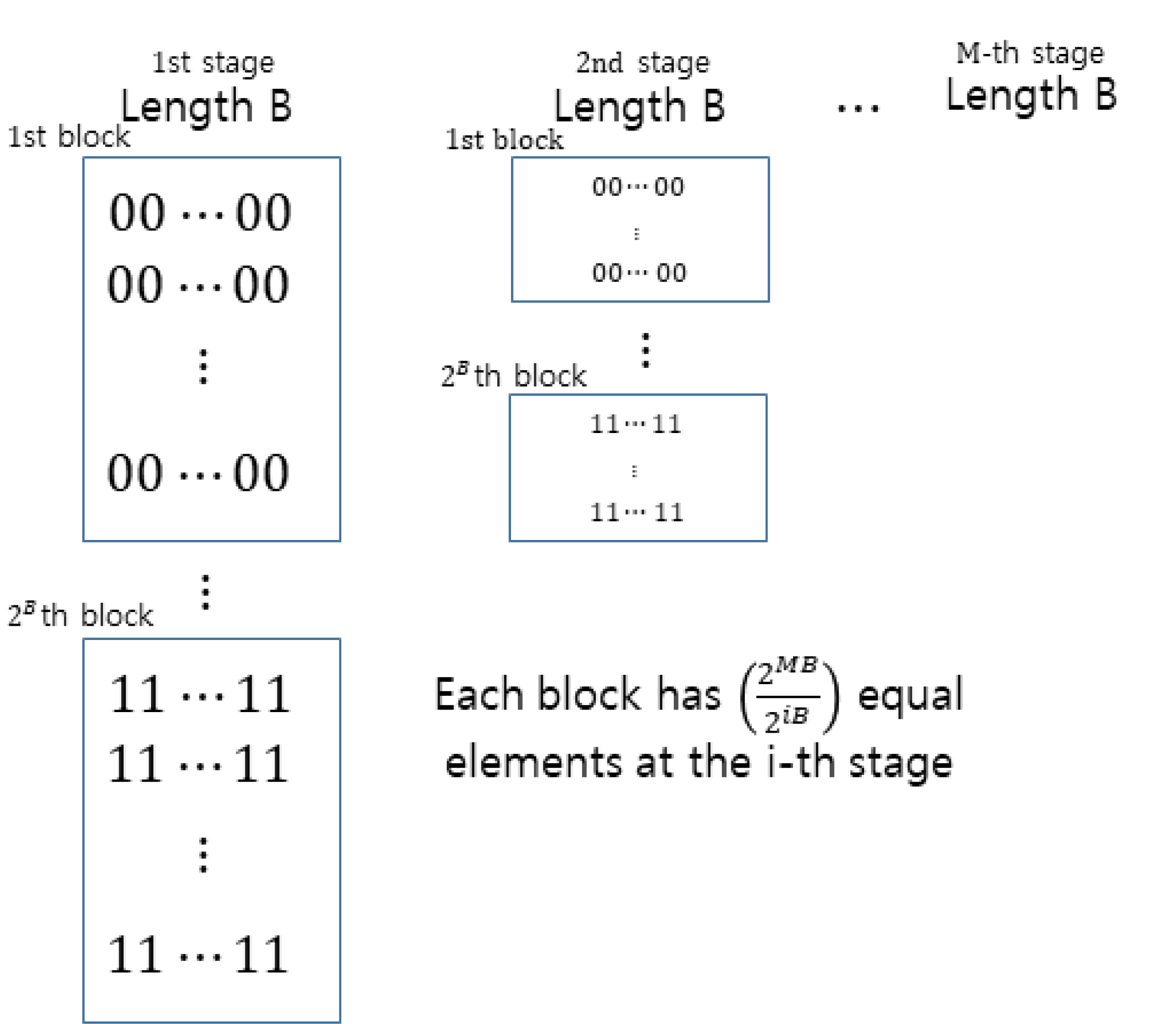
DNN을 통한 MIMO채널의 압축과정은 채널 정보를 양자화한 결과이므로, 각 사용자가 피드백하는 양자화 비트열은 채널의 정보를 내포하고 있다. 하지만 이러한 비트열은 채널의 형태와는 표면적으로 무관하기 때문에 송신부 DNN에 블라인드 형태로 입력하여 적절한 프리코딩 행렬을 얻을 수는 있지만, 그 자체로는 채널에 관한 정보로써 사용할 수 없다(이러한 정보를 implicit 채널 정보라고 칭한다). 따라서 송신부에서 사용자의 피드백 비트를 모두 모은 후, 해당 비트 자체를 관찰하여 적절한 사용자를 선택하는 것은 불가능하다. 이를 해결하기 위해 본 연구에서는 스케줄링 과정에서 송신부와 사용자들이 서로 handshaking 과정을 거치는 기회적(opportunistic)방법(기회적 방법의 기본 개념에 관해서는 [3]와 [3]에서 참조한 관련 논문을 참고할 수 있다)을 활용한다. 요컨대, 본 연구에서 제안하는 알고리즘은 다음과 같은 multi-stage handshaking 구조를 가진다. 프리코딩 및 스케줄링에 활용되는 송수신부 DNN들은 [2]와 동일한 과정으로 K = M을 가정하고 사전에 학습한다. 송신부 DNN은 MB의 길이를 가지는 비트 열의 조합을 입력받으며, 조합된 비트열에 상응하는 프리코딩 행렬을 lookup 테이블의 형태로 출력한다. 본 연구에서 제안하는 스케줄링 기법은 단계적 handshaking 구조를 활용하므로, 송신부 DNN의 lookup 테이블을 계층구조로 구성하는 것을 선행 조건으로 한다. 송신부 DNN의 입력은 MB길이의 비트열이므로 총 2^MB개의 서로 다른 입력이 존재한다. 따라서 제안하는 lookup 테이블은 2^MB개의 행으로 입력 비트열을 구분하고, 각 행은 MB길이의 비트열로 구성된다. 또한, 각 행을 M개의 부비트열로 나누며, 각 부비트열은 B의 길이를 가진다. 제안하는 스케줄링은 M개의 stage를 통해 각 stage에서 단계적, 기회적으로 사용자를 한 명씩 선택하며, 그 과정에서 선택된 사용자에게 가장 적합한 부비트열을 정한다. 즉, 제안하는 방법은 M개의 stage를 사용하여, 순서대로 M개의 부비트열을 결정하는 과정으로 해석할 수 있다.

이를 위해, 제안하는 lookup 테이블도 M개의 stage로 나뉜 계층구조를 통해 재배치된다. 첫 번째 stage는 2^MB개 의 행을 2^B개의 블록으로 나누되, 각 블록의 첫 번째 부 비트열은 모두 동일하도록 분류한다(그림 1). 두 번째 stage에서 는 첫 번째 스테이지에서 나눈 각 블록을 다시 2^B개의 블록으로 나누되, 두 번째 stage의 각 블록은 2번째 부비트열이 동일하도록 분류한다. 동일한 방법으로 i번째 stage에서는 i-1번째 stage에서 분류된 블록을 다시 2^B개의 블록으로 나누되, i번째 stage의 각 블록은 i번째 부비트열이 동일하도록 분류한다. 즉, i번째 stage의 각 블록은 동일한 2^MB/2^iB개의 부비트열의 묶음이 차례로 나열된다.

그림 1.

송신부 DNN에 대한 입력 비트열Fig. 1. Input sequence design to the TX DNN

이와 같이 계층적으로 구성된 lookup 테이블을 모든 DNN이 공유하는 것으로 가정하고 스케줄링 알고리즘은 다음과 같이 구성된다. 스케줄링의 첫 번째 stage에서는 각 사용자가 자신이 단독으로 선택되었다고 가정하였을 때, 가장 SINR이 높은 블록을 첫 번째 부비트열로 결정한다. 첫 번째 부비트열이 결정되면 이어지는 stage에서는 해당 부비트열을 포함하는 블록을 제외한 나머지 행은 최종 후보군에서 제외한다. 두 번째 stage에서는 본인이 첫 번째 사용자로 뽑혔다고 가정한 상태에서, 총 두 명의 사용자가 뽑혔다고 가정하고 SINR을 계산 후, 자신의 SINR이 가장 높은 프리코딩 행렬에 해당하는 두 번째 stage의 블록을(첫 번째 stage에서 선택된 첫 번째 부비트열을 포함하지 않는 후보들은 제외되었기 때문에, 고려대상인 후보들은 첫 번째 부비트열이 모두 동일한 상황) 두 번째 부비트열로 결정한다. 이와 같은 방식으로 M개의 부비트열을 모두 결정하면, 각 사용자는 자신이 원하는 MB개의 비트열을 각각 독립적으로 결정할 수 있다. 또한, 각 사용자는 1명이 뽑혔을때부터, M명이 뽑혔을때까지 M개의 서로 다른 SINR 값을 자신의 CQI로 사용한다. 기회적 피드백 및 스케줄링의 첫 번째 단계에서는 이렇게 결정된 MB개의 비트열과 M개의 CQI를 각 사용자가 피드백한다. 이 경우, 전체 피드백 비트의 양이 CQI를 무시할 경우에도 MBK로 K에 선형 비례하여 증가하므로, 사용자 수에 따라서는 막대한 양의 피드백 비트가 발생하게 된다. 따라서 실제 환경에서는 [3]에서 연구된 바와 같이 적절한 임계값을 CQI값에 적용하여 실질적으로 피드백을 수행하는 사용자의 수를 제한한다. 즉, 첫 번째 stage에서는 첫 번째 CQI가 임계값보다 큰 사용자들로부터만 피드백을 받게 되며, 그 중 첫 번째 CQI가 가장 큰 사용자를 첫 번째 사용자로 선택한다. 선택된 사용자는 이미 MB개의 비트열을 피드백하였기 때문에, 기지국에서는 lookup 테이블을 통해 상응하는 프리코딩 행렬을 바로 계산할 수 있다. 송신부는 이렇게 첫 번째로 선택된 사용자의 M개의 프리코딩행렬과 M개의 CQI를 사용자에게 브로드캐스트하고, 이후 2번째부터 M번째 사용자의 선택은 공유된 프리코딩 행렬과 CQI들을 확인하여 순차적으로 결정된다. 첫 번째 사용자가 공유한 M개의 CQI를 편의상 γ₁₁,γ₁₂, ... , γ_1M로 표기하며, γ_1j는 j명이 최종적으로 스케줄링 되었다고 가정하였을 때, 첫 번째 사용자가 제공하는 SINR값에 해당한다. 이어서 두 번째 stage에서는 브로드캐스트된 프리코딩 행렬을 통해 본인이 두 번째 사용자로 선택되었을 때 확보가능한 SINR값을 최종 선택된 유저가 2명인 경우부터 M명인 경우까지 M-1개의 경우에 대해 각각 계산하여 M-1개의 CQI를 피드백한다. 이 때, 두번째 유저의 CQI를 편의상 γ₂₂,γ₂₃, ... , γ_2M로 표기하며 γ_2j는 j명이 최종적으로 스케줄링 되었다고 가정하였을 때, 두 번째 유저가 제공하는 SINR값에 해당한다. 동일한 요령으로 M명의 사용자를 연속적으로 선택하며, M번째 사용자는 본인이 마지막 사용자이므로 하나의 CQI γ_MM를 피드백한다. 이와같은 M단계의 피드백 및 스케줄링이 마무리되면, 송신부는 log₂(1+γ_ij)를 i,j번째 원소로 가지는 upper triangular 행렬을 구성할 수 있으며, 이 행렬의 각 열벡터가 하나의 스케줄링 조합에 상응한다. 즉, 총 M개의 스케줄링 조합이 있으며, 그 중 sum rate 기대치(각 열벡터 별로 자신의 원소들을 총합한 것)가 가장 높은 조합을 제공하는 사용자들을 선택하여 스케줄링을 마무리한다.

Ⅳ. 시뮬레이션 결과 및 결론

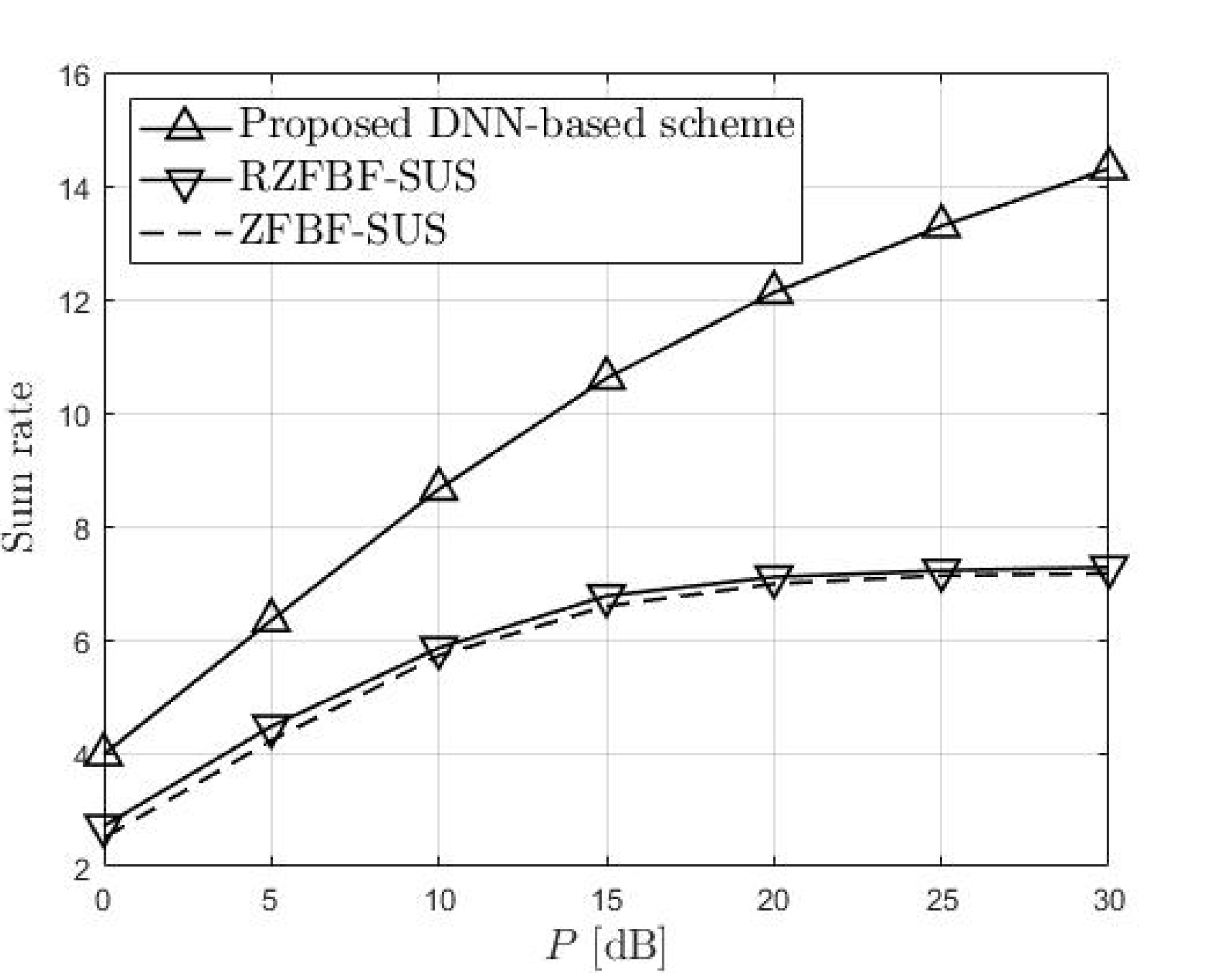
그림 2는 파라미터가 M=8, B=3, K=200일 때, 제안하는 DNN기반의 스케줄링과 기존의 코드북 기반의 프리코딩 기법의 성능을 비교하고 있다. 채널추정에는 [2]에서 사용된 것과 같은 방식을 사용하며, 추정을 위한 training sequence의 길이는 L=6으로 설정되엇다. 제안하는 스케줄링 기법이 기존대비 높은 성능을 보이는 이유는 크게 두 가지로 요약할 수 있다. 첫째는 [2]에서 논의된 바와 같이 채널 추정, 양자화, 피드백, 프리코딩과정의 통합최적화가 반영되었기 때문이다. 두 번째는 DNN기반의 방식이 orthogonal한 프리코더를 활용하지 않음에도 불구하고 lookup 테이블의 결과를 공유함으로써 현재채널 대비 기대되는 sum rate의 값을 정량적으로 측정할 수 있기 때문이다.

그림 2.

송신 파워 vs. Sum rateFig. 2. Transmit power vs. Sum rate

References

• Min, M., On Regularization Parameter for Block Diagonalization with Limited Feedback, The Journal of KCIS., (2021, July), 46(7), p1156-1159. [https://doi.org/10.7840/kics.2021.46.7.1156]
• Kong, K., Song, W. J., Min, M., Knowledge Distillation-Aided End-to-End Learning for Linear Precoding in Multiuser MIMO Downlink Systems With Finite-Rate Feedback, IEEE Trans. on Vehicular Tech., (2021, Oct.), 70(10), p11095-11100. [https://doi.org/10.1109/TVT.2021.3110608]
• Min, M., Kim, D., Kim, H. M., Im, G. H., Opportunistic two-stage feedback and scheduling for MIMO downlink systems, IEEE Trans. on Commun., (2013, Jan.), 61(1), p312-324. [https://doi.org/10.1109/TCOMM.2012.092612.120024]