곱셈 연산을 고려한 고속 역변환 방법

Ⅰ. 서 론

일반적인 하이브리드 블록 기반 비디오 압축은 입력된 2차원 영상 신호를 여러 개의 블록으로 나누어 각 블록에 화면 내 예측 또는 화면 간 예측, 변환 및 양자화, 엔트로피 코딩 등의 과정을 적용하여 압축을 진행한다. 이중 변환 부호화는 예측 단계로부터 생성되는 잔차 신호에 적용되며, 공간 영역의 잔차 신호를 주파수 영역으로 변환함으로써 저주파 영역으로 에너지를 압축하여 이후 엔트로피 코딩 과정에서 더 효율적으로 압축할 수 있게 한다.

최근 4K 영상, UHD(Ultra High Definition) 영상과 같은 고화질, 고해상도 영상의 수요와 공급이 증가하고, 화상 회의, 비디오 스트리밍과 같은 서비스 시장의 성장으로 더 높은 압축 효율을 가지는 비디오 압축 기술의 필요성이 대두되고 있다. 최신 비디오 코딩 표준인 VVC(Versatile Video Coding)^[1]는 ITU-T VCEG(Video Coding Experts Group)과 ISO/IEC MPEG(Moving Picture Experts Group)이 공동으로 창설한 JVET(Joint Video Exploration Team)에서 이전 표준인 HEVC(High Efficiency Video Coding)^[2] 대비 2배의 압축 성능을 목표로 개발하였고, 2020년 7월 표준화가 완료되었다. VVC는 UHD 영상, HDR(High Dynamic Range) 영상, WCG(Wide Color Gamut) 영상, 스크린 콘텐츠 영상, 360º 영상 등 다양한 영상을 대해 지원하며, 압축 성능을 높이기 위해 기존의 비디오 코딩에서 사용되지 않았던 여러 새로운 기술이 도입되었다. HEVC에서 사용된 QT(Quaternary Tree) 방식에 BT(Binary Tree)와 TT (Ternary Tree)를 더한 MTT(Multi-Type Tree)와 휘도와 색차 성분의 분할을 서로 다르게 가지는 dual tree^[3], 화면 내 예측에서 3개의 참조 샘플 라인 중 하나를 선택하여 사용하는 MRL(Multiple Reference Lines)^[4], BM(Bi-lateral Matching) 기반 움직임 벡터 탐색 과정을 통해 merge mode의 예측 정확도를 높이는 DMVR(Decoder side Motion Vector Refinement)^[5], 주변환 이후 변환 계수에 한 번 더 변환을 적용하는 LFNST(Low Frequency Non-Separable Transform)^[6], 원본 영상과 복원 영상의 오차를 최소화하는 최적의 필터 계수를 유도하여 필터링하는 ALF(Adaptive Loop-Filter)^[7] 등 다양한 분야에서 새로운 기술이 채택되었다. 그러나 이러한 새로운 기술의 도입으로 VVC의 부호화기와 복호화기의 복잡도가 상당히 증가하였으며 이에 따라 부호화 성능을 유지하면서 복잡도 감소를 위한 방법이 필요하다.

본 논문에서는 부호화 과정 및 복호화 과정에서 연산량을 줄이기 위해 선형 변환의 선형성을 이용한 고속 역변환 방법을 제안한다. 제안하는 방법은 역양자화 및 역이차변환 이후 역주변환 과정에서 곱셈 연산량에 따라 제안하는 방법과 기존의 역변환 방법을 선택적으로 사용한다.

본 논문은 다음과 같이 구성한다. 2장에서는 변환 부호화에 관해 설명하고, 3장에서는 제안하는 고속 역변환 방법을 설명한다. 그리고 4장에서는 실험 결과를 분석하고, 5장에서 결론을 맺는다.

Ⅱ. 변환 부호화

변환 부호화는 공간 영역의 잔차 신호를 주파수 영역으로 변환함으로써 저주파 영역에 에너지를 집중시켜 압축하는 방법으로, 적은 계수에 더 많은 에너지를 집중시킬수록 효율적인 변환이다. 일반적으로 자연 영상에서 입력된 신호는 주변 화소들과 높은 상관관계를 가지기 때문에 변환을 통해 변환 계수들 간의 상관관계를 낮추는 방식으로 압축을 수행한다. 비상관화 측면에서 가장 최적의 변환은 KLT(Karhunen-Loève transform)라고 알려져 있다. 하지만 KLT는 변환 기저가 입력 신호에 의존적이고, 복잡도가 높아서 실제 비디오 압축 표준에서는 잘 쓰이지 않는다. DCT(Discrete Cosine Transform)가 KLT를 잘 근사하기 때문에 대부분의 비디오 코딩 표준에서는 DCT-2(Discrete Cosine Transform type 2)^[8]와 같은 고정 기저를 사용한다. 이처럼 고정 기저를 사용하는 경우, 변환 기저 값이 모두 고정된 상숫값이기 때문에 변환 기저에 대한 정보를 따로 전송할 필요가 없다. DCT-2는 입력 신호가 균질한 경우 좋은 성능을 보여주지만, 자연 영상의 다양한 특성 때문에 DCT-2가 잘 동작하지 않는 경우도 존재한다. 이를 보완하기 위해 여러 변환 기저를 사용하는 방법들이 제안되었다. HEVC에서는 화면 내 예측으로 생성된 44블록에 한해 DST-7(Discrete Sine Transform type 7)을 사용한다^[9].

VVC의 변환 부호화 관련 기술^[10]은 주변환, 이차변환, 변환 스킵 등이 있다. 주변환은 기존의 비디오 압축에서 사용되었던 기술로 예측 후 잔차 신호에 변환 기저를 적용하여 변환 계수를 얻는 기술이다. VVC의 주변환은 직전 비디오 압축 표준인 HEVC와 비교하였을 때, 최대 CTU(Coding Tree Unit)의 크기가 128로 증가함에 따라 최대 변환 크기도 32에서 64로 증가하였다. DCT-7의 적용 범위가 확대되었으며, DCT-8 (Discrete Cosine Transform type 8)이 새로운 변환 기저로 추가되었다. DCT-2는 최대 64-point까지 적용할 수 있고, DST-7과 DCT-8은 최대 32-point까지 적용할 수 있다. 변환 시 가로 방향과 세로 방향의 변환 기저를 서로 다른 변환 기저를 선택할 수 있다. VVC의 주변환은 MTS(Multiple Transform Selection)라고도 불린다. MTS는 휘도 성분에만 적용 가능하며, 색차 성분은 기존과 같이 DCT-2를 사용하여 변환을 수행한다. 수식 (1)은 1차원 N-point 변환을 나타내고, 수식 (2)는 1차원 N-point 역변환을 나타낸다.

여기서 F(u)는 변환된 신호를 의미하고, p(x)는 입력되는 신호를 의미하고, v_u,x는 변환 기저를 의미한다. 수식 (3), (4)는 1차원 N-point DCT-2, (5), (6)은 각각 1차원 N-point DST-7, 1차원 N-point DCT-8의 변환 기저를 나타낸다.

변환의 크기가 커짐에 따라 고해상도 영상 부호화의 효율이 높아졌지만, 계산 복잡도가 증가하였다. 이를 해결하기 위해 고주파수 영역에 있는 변환 계수를 0으로 만드는(zero-out) 방법을 채택하여 계산 복잡도를 낮췄다. Zero-out은 64-point DCT-2와 32-point DST-7, DCT-8에만 적용된다. 64-point DCT-2의 경우 인덱스가 32보다 작은 경우에만 계수가 유지되고 나머지 계수들은 모두 0이 된다. 32-point DST-7, DCT-8의 경우 인덱스가 16보다 작은 경우에만 계수가 유지되고 나머지 계수들은 모두 0이 된다. MTS는 explicit MTS와 implicit MTS로 구분할 수 있다. Explicit MTS는 선택된 변환 기저를 MTS index를 통해 명시적으로 시그널링하고, implicit MTS는 부호화된 정보를 기반으로 변환 기저를 선택한다.

이차변환은 주변환을 통해 얻은 변환 계수에 다시 변환을 적용하여 추가로 중복성을 제거하는 기술이다. 이차변환은 잔차 신호의 왼쪽 위의 저주파 영역에 있는 계수에만 적용되며, 주변환과 달리 비분리 변환을 사용하여 LFNST라고 명명되었다. 이차변환은 화면 내 예측으로 생성되고, 가로, 세로 방향의 변환 기저가 모두 DCT-2인 경우에만 적용할 수 있다. 변환 블록의 크기에 따라 이차변환이 적용되는 영역이 달라지며, 변환 기저도 달라진다.

Ⅲ. 제안하는 고속 역변환 방법

변환 및 역변환은 행렬 곱셈 또는 고속 변환 방법을 통해 구현될 수 있다. 대부분의 비디오 압축 표준에서는 연산량을 줄이기 위해 2차원 변환을 가로, 세로 방향의 1차원 변환으로 나눠서 수행한다. 행렬 곱셈을 이용하는 경우 1차원 N-point 변환에 대해 N²번의 곱셈 연산이 필요하다. 고속 변환 방법은 주로 변환 기저의 특성을 이용하여 연산 횟수를 줄이는 방법을 이용한다. DCT-2의 경우 짝수 번째 기저 벡터는 대칭성을 지니고, 홀수 번째 기저 벡터는 반 대칭성을 가지는 특성을 이용하여 고속 변환 방법을 구현할 수 있다^[9]. DST-7과 DCT-8의 경우도 마찬가지로 변환 기저의 특성을 이용하여 고속 변환 방법을 사용할 수 있다^[11]. 이러한 변환 기저의 특성을 이용한 고속 변환 방법은 해당 기저에만 적용할 수 있다는 단점이 있다.

본 논문에서는 선형 변환의 선형성을 이용하여 역변환 시 계산량을 줄이는 고속 역변환 방법을 제안한다. 제안하는 방법은 주변환에 적용되며, 변환 기저 종류와 관계없이 적용할 수 있다. 현재 VVC의 주변환에서 사용하는 DCT-2, DST-7, DCT-8은 모두 정규직교 기저로 역변환은 변환의 전치 행렬을 통해 수행할 수 있으며, 분리 가능한 기저이기 때문에 2차원 변환을 가로, 세로 방향으로 1차원 기저를 적용하여 수행할 수 있다.

2차원 변환을 두 번의 1차원 변환으로 분리하여 수행하는 경우, 가로의 길이가 m, 세로의 길이가 n인 블록 Y에 대해, 세로 방향 기저가 A, 가로 방향 기저가 B인 경우 역변환 과정을 수식 (7)과 같이 표현할 수 있다.

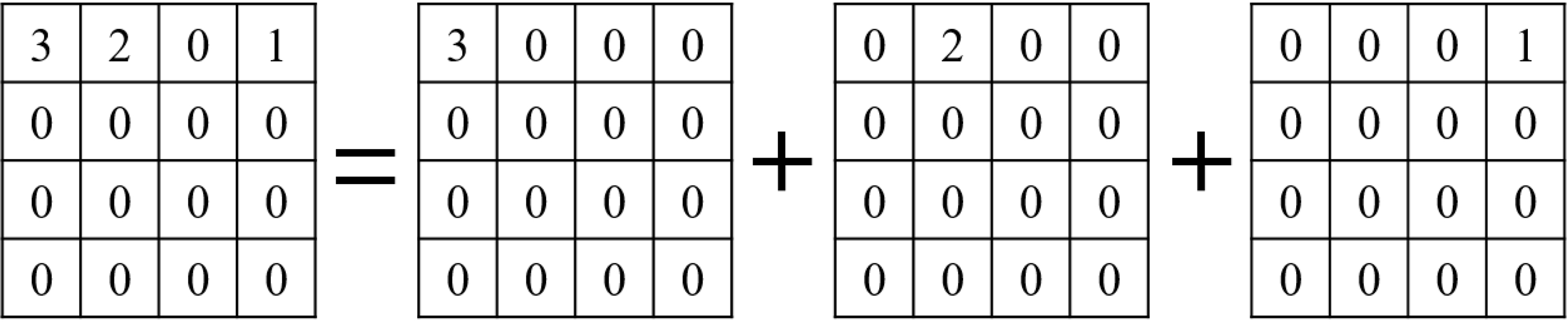
수식 (7)에서 X^'는 역변환된 블록을 의미한다. 블록 Y가 0이 아닌 계수 N개로 이루어진 경우, Y는 수식 (8)과 같이 Y와 같은 크기의 단 한 개의 0이 아닌 계수를 가지는 N개의 서브 블록의 합으로 표현할 수 있다.

그림 1은 3개의 0이 아닌 계수를 가지는 4×4블록을 서브 블록의 합으로 표현하는 예시를 보여준다. 현재 VVC에서 주변환 기저로 사용하는 DCT-2, DST-7, DCT-8은 모두 선형 변환이기 때문에 다음과 같은 성질을 가진다.

그림 1.

4×4블록의 분할 예시Fig. 1. Example of 4×4 block

수식 (9)에서 T는 변환을 의미하고, x, y는 변환의 입력, a, b는 임의의 상수이다. 수식 (8)과 수식 (9)를 이용하여 수식 (7)의 역변환 과정을 다시 표현하면 아래 수식 (10)과 같다.

제안하는 역변환 방법의 계산은 다음과 같다. 먼저, N개의 0이 아닌 계수를 가지는 블록 Y를 단 1개의 0이 아닌 계수를 가지는 서브 블록으로 분리한다. 각 서브 블록에 대해 역변환을 수행한 후, 그 결과를 모두 합해 최종 역변환 결과를 생성한다. 하나의 서브 블록에 대해 역변환을 수행하는 방법은 다음과 같다. 가로 길이가 m, 세로 길이가 n인 서브 블록 y_l(1 ≤ l ≤ N)의 (i, j)번째 위치에 0이 아닌 계수 x_i,j가 존재할 때, y_l에 대한 역변환은 아래 수식 (11)과 같이 계산할 수 있다.

수식 (11)에서 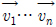은 A^T의 기저 벡터, 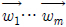은 B의 기저 벡터를 의미한다. 먼저 A^Ty_l을 계산하면 수식 (12)와 같이 결과 행렬의 j번째 열을 제외한 나머지 열은 모두 0이 되고, j번째 열에만 0이 아닌 값이 존재하게 된다.

수식 (12)에서 v_i,j는 A^T의 i번째 기저 벡터 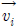의 j번째 원소를 의미한다. 수식 (12)에서 구한 A^Ty_l를 이용하여 최종적으로 A^Ty_lB 를 계산하면 수식 (13)과 같이 된다.

수식 (13)에서 w_i,j는 B의 i번째 기저 벡터 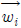의 j번째 원소를 의미한다. 제안하는 역변환 방법을 사용하여 하나의 서브 블록에 대해 역변환 수행 시, 수식 (12)에서 n개의 곱셈이 필요하고, 수식 (12)의 계산 결과를 활용하여 수식 (13)을 계산하면 (n × m)개의 곱셈이 필요하다. 따라서 하나의 서브 블록을 역변환하는 데 필요한 곱셈 연산 수는 (n + (n × m))개이고, N개의 0이 아닌 계수를 가지는 변환 블록에 대해 필요한 곱셈 연산 수는 총 N × (n + (n × m))개다.

기존의 변환 방법과 제안하는 선형성을 이용한 역변환 방법 중 어느 것을 사용하여 역변환을 수행할지는 곱셈 연산량에 따라 결정된다. 변환 블록에 대하여 제안하는 방법으로 역변환 수행 시 VVC 참조 소프트웨어인 VTM(VVC Test Model)에 구현된 역변환보다 곱셈 연산량이 적거나 같은 경우에만 제안하는 선형성을 이용한 역변환 방법으로 역변환을 수행한다. 제안하는 고속 역변환 방법의 총연산량은 변환 블록 내의 0이 아닌 계수의 개수(N)에 따라 달라진다. 따라서 VVC에서 가능한 모든 변환 블록 크기에 대해 현재 VTM에서 사용되고 있는 역변환 방법의 곱셈 횟수를 계산하고, 이를 이용하여 모든 블록 크기에 대한 임곗값을 계산하였다. 임곗값은 각 블록 크기에 대해 제안하는 방법의 곱셈 횟수가 현재 VTM의 곱셈 횟수보다 작거나 같게 되는 최대의 0이 아닌 계수의 개수(N)로 결정하였다. 블록 내의 0이 아닌 계수의 개수가 임곗값 이하인 경우 제안하는 방법을 사용하여 역변환을 수행하고, 임곗값을 초과하는 경우 기존 방법을 사용하여 역변환을 수행한다. 역변환을 수행하기 전 반복문을 이용하여 블록 내의 0이 아닌 계수의 개수를 세고, 개수가 임곗값을 초과하는 즉시 반복문을 종료하고 기존 방법을 이용하여 역변환을 수행한다. 제안하는 방법은 이미 부호화된 정보와 소프트웨어 안에 내장된 변환 기저를 사용하기 때문에 추가적인 플래그가 필요 없다. 제안하는 방법을 부호화기와 복호화기에 적용된다. VVC는 변환 및 역변환 과정 중 16비트 내에서 연산이 수행되도록 절삭 연산을 수행한다. 기존 방법의 경우 각 방향의 역변환을 수행한 후 절삭 연산을 수행하므로, 총 2번의 절삭 연산이 역변환 과정 중에 필요하다. 제안하는 방법은 블록에 대해 가로, 세로 방향의 역변환을 모두 수행한 뒤 1번의 절삭 연산을 수행한다. 절삭 연산의 차이로 인해 하나의 블록에 대해 역변환을 수행할 때, 기존 방법을 사용하여 역변환을 수행하는 결과와 제안하는 방법을 이용하여 역변환을 수행한 결과 간의 차이가 발생할 수 있다.

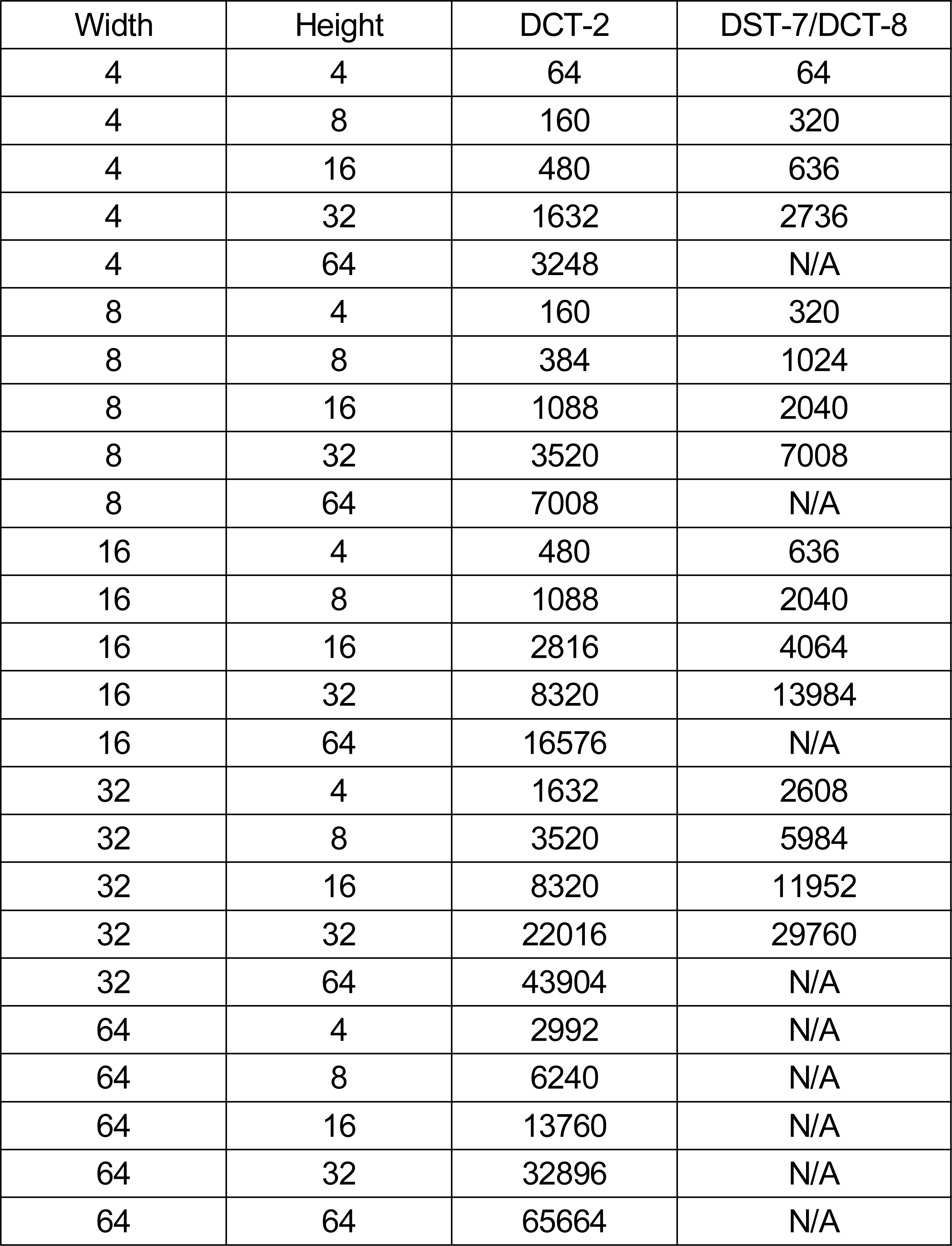
표 1은 VTM-8.2(VVC Test Model-8.2)^[12]에서 블록 크기에 따라 역변환을 수행하는 데 필요한 곱셈양을 나타낸 표이다. 첫 번째 열과 두 번째 열은 각각 블록의 가로, 세로 길이를 나타내고, 세 번째 열은 가로, 세로 방향의 변환 기저가 모두 DCT-2인 경우의 곱셈 횟수, 마지막 열은 가로, 세로 방향의 변환 기저가 모두 DST-7 또는 DCT-8인 경우의 곱셈 횟수를 나타낸다.

표 1.

VTM-8.2에서의 곱셈 연산량Table 1. The number of multiplications in VTM-8.2

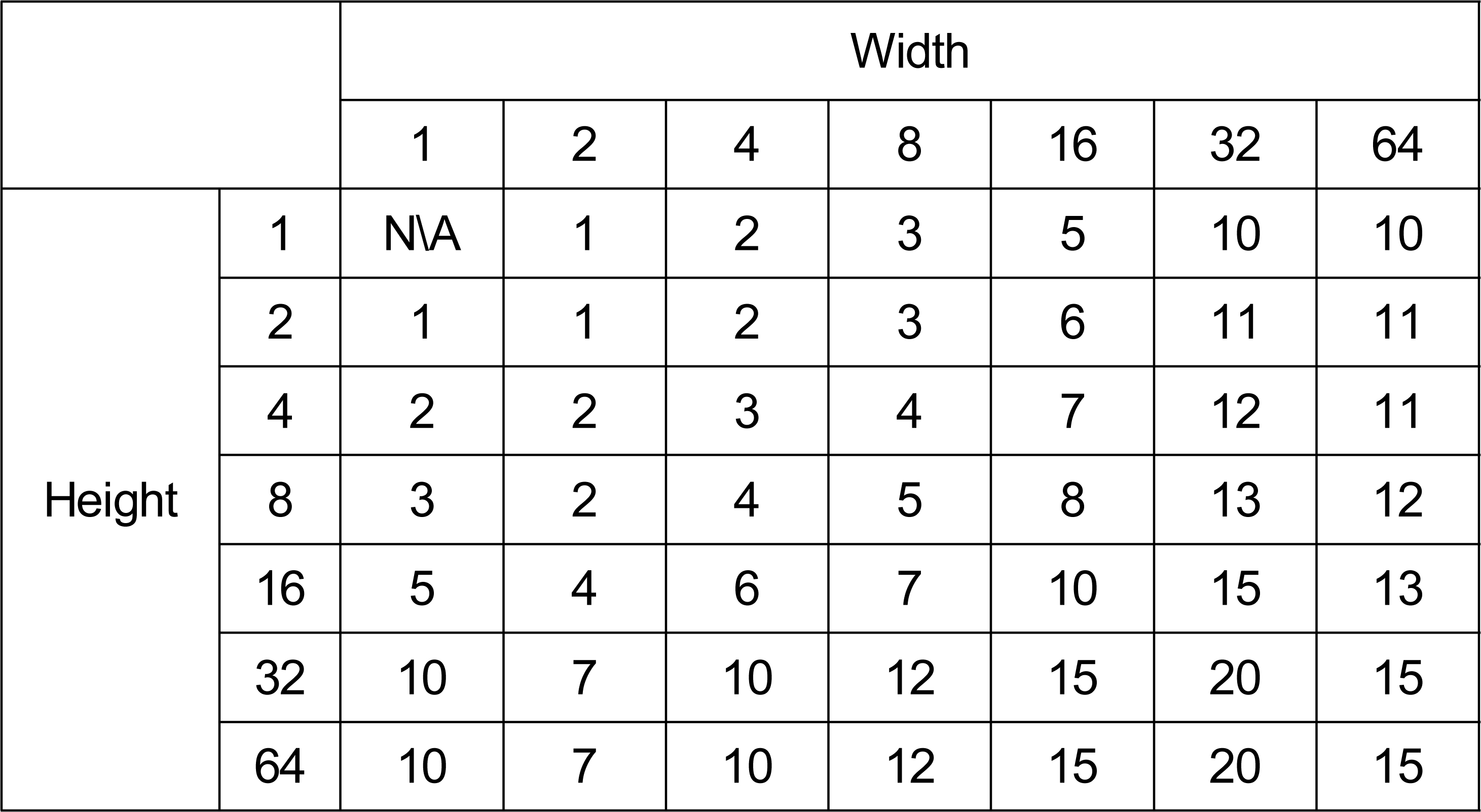
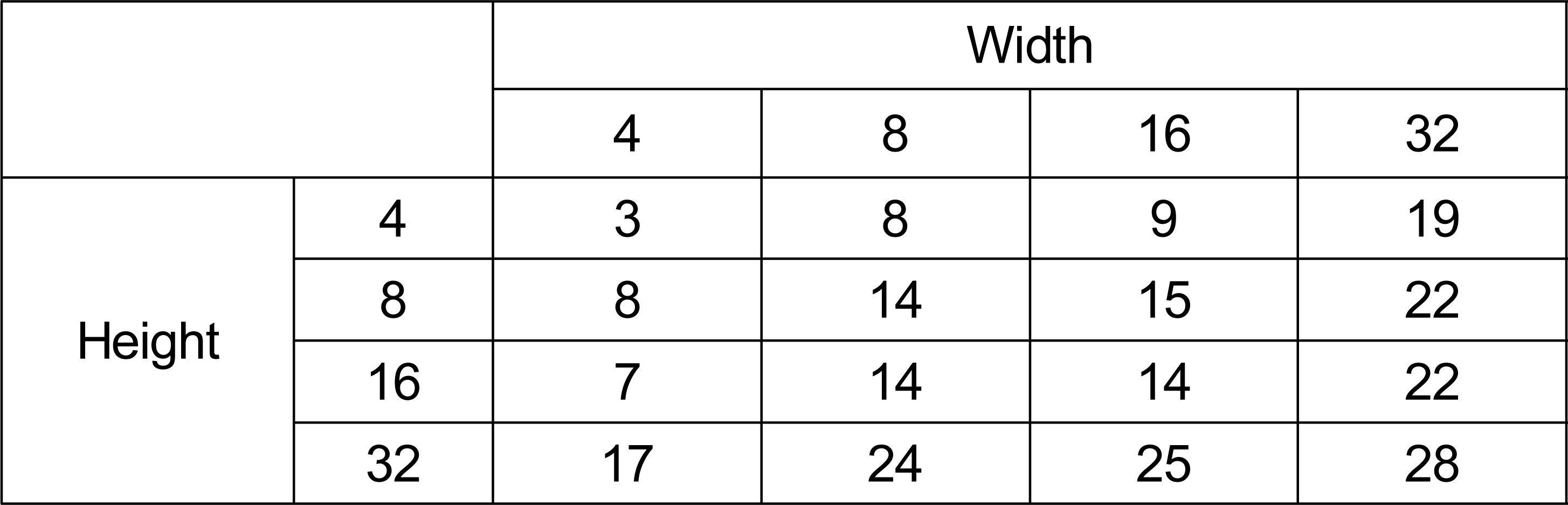
표 2와 3은 각 블록 크기에 대한 임곗값을 나타내는 표이다. 표 2는 가로, 세로 변환 기저가 모두 DCT-2인 경우와 비교하여 결정된 임곗값이고, 표 3은 가로, 세로 변환 기저가 모두 DST-7 또는 DCT-8인 경우와 비교하여 결정된 임곗값이다. 가로, 세로 변환 기저가 DCT-2와 DST-7 또는 DCT-8의 조합으로 이루어진 경우 표 2의 임곗값을 사용한다.

표 2.

가로, 세로 변환 기저가 모두 DCT-2 이거나 DCT-2와 DST-7 또는 DCT-8의 조합인 경우 블록 크기 별 임곗값Table 2. Threshold representing the number of non-zero coefficients in each block size, when the horizontal and vertical kernels are DCT-II/DCT-II or other combinations listed in Table 5

표 3.

가로, 세로 변환 기저가 모두 DST-7 또는 DCT-8의 조합인 경우 블록 크기 별 임곗값Table 3. Threshold representing the number of non-zero coefficients in each block size, when the horizontal and vertical kernels are a combination of DST-VII and DCT-VIII (DST-VII/DCT-VIII).

Ⅳ. 실험 결과 및 분석

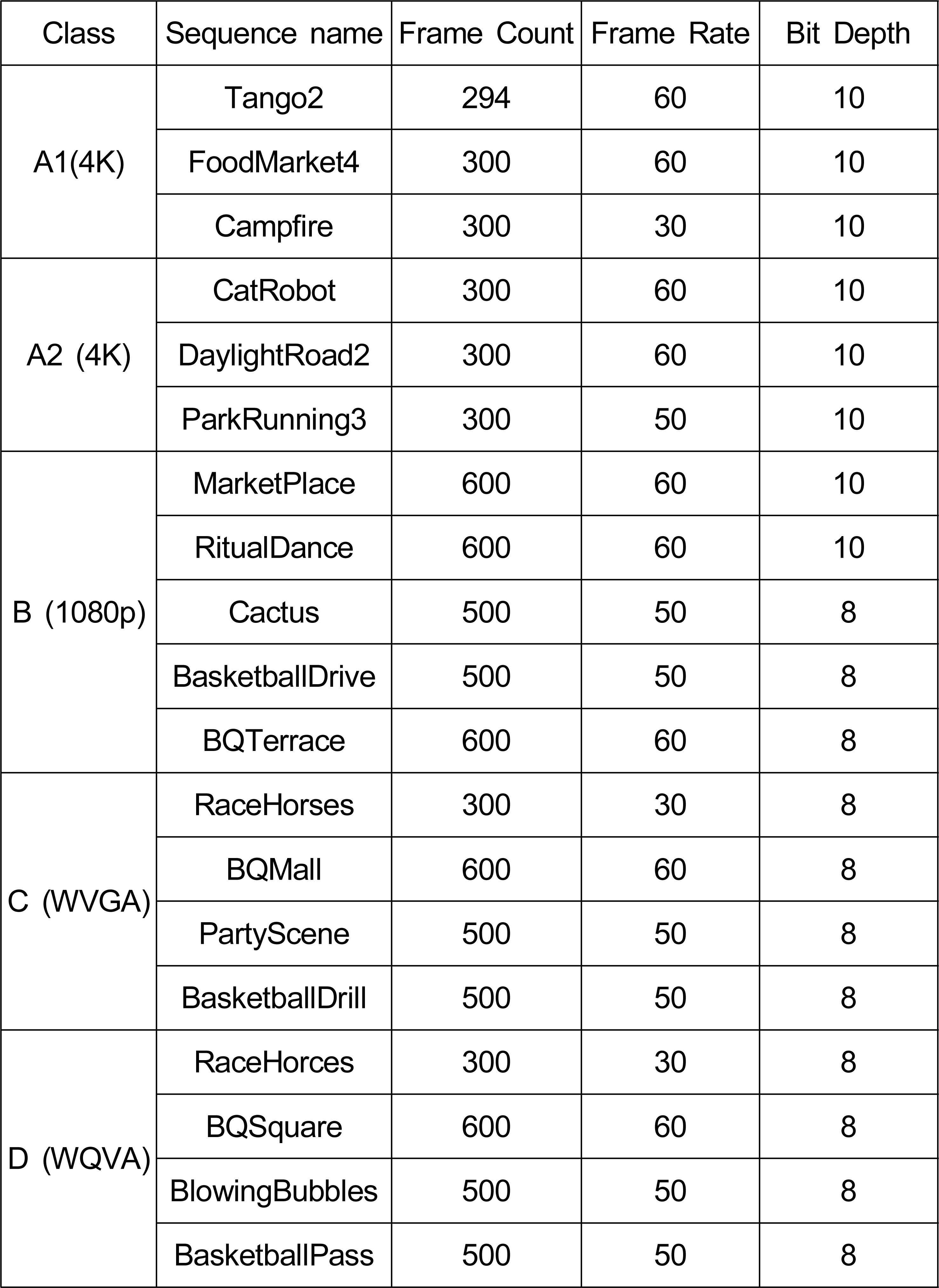
본 장에서는 제안하는 곱셈 연산을 고려한 선형성을 이용한 역변환 방법에 대한 성능을 보인다. 제안하는 고속 역변환 방법은 VTM-8.2에 구현되었다. 실험은 VVC 공통 실험 조건(Common Test Condition)^[13]에 따라 AI(All Intra)와 RA(Random Access) 부호화 환경에서 진행되었다. 실험에 사용된 양자화 파라미터(QP)는 22, 27, 32, 37이다. 실험에 사용한 영상은 표 4와 같다. 표 4에서 4K는 3840 × 2160, 1080p는 1920 × 1080, WVGA는 832 × 480, WQVGA는 416 × 240 해상도의 영상이다.

표 4.

실험에 사용된 영상 정보Table 4. Information on video sequence

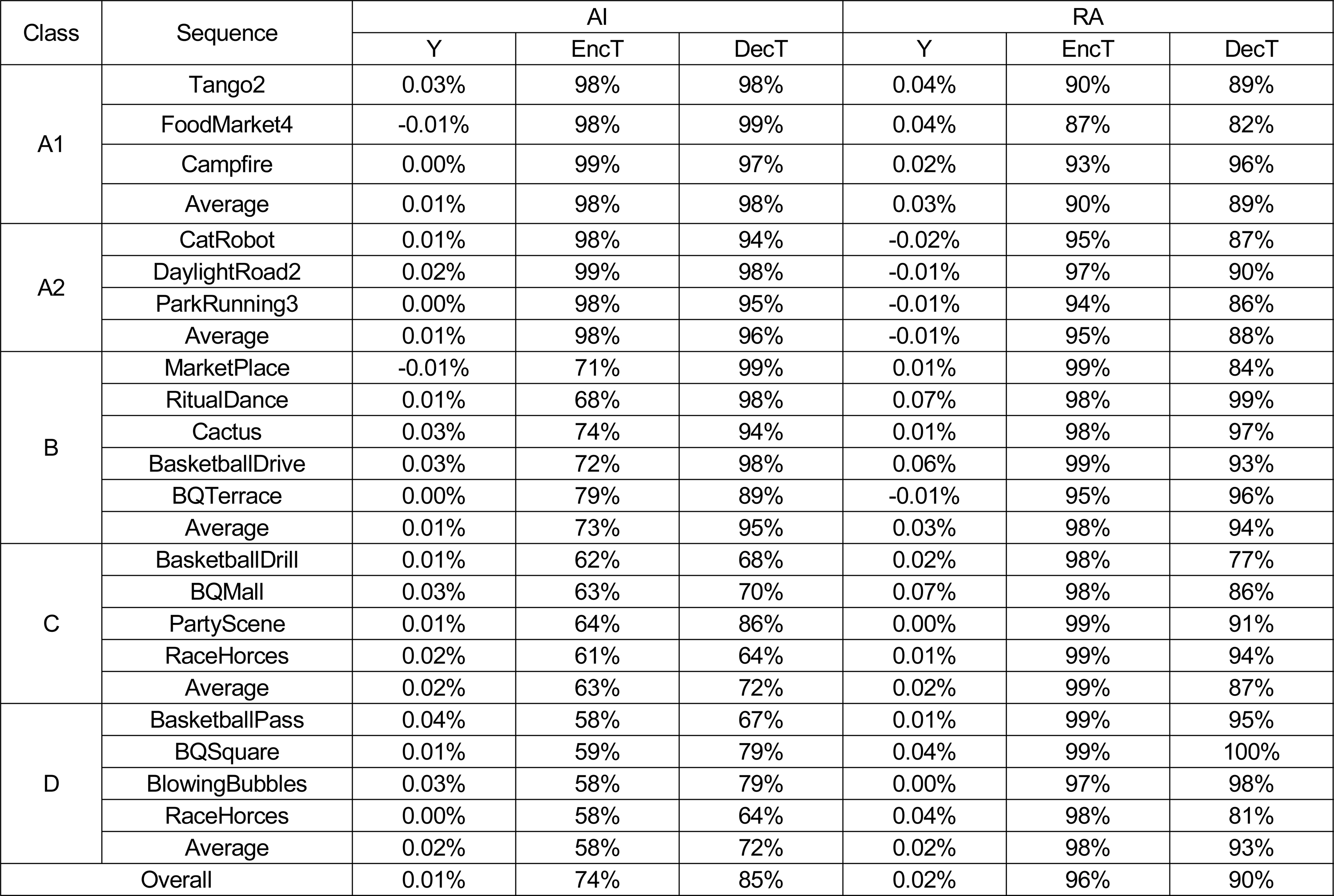
표 5는 제안하는 방법과 VTM-8.2의 부호화 성능과 계산 복잡도를 비교한 결과이다. 부호화 시간 EncT와 복호화 시간 DecT는 다음 수식 (14)와 같이 계산된다.

표 5.

실험 결과Table 5. Experimental result

제안하는 방법은 기존 방법 대비 약간의 BD-rate 손실을 일으켰지만, 부호화 시간과 복호화 시간을 AI에 대해 각각 26%, 15%, RA에 대해 각각 4%, 10% 감소했다. 또한, 저해상도 영상인 class C, D에 대해 복호화 시간이 많이 감소한 것을 확인할 수 있다.

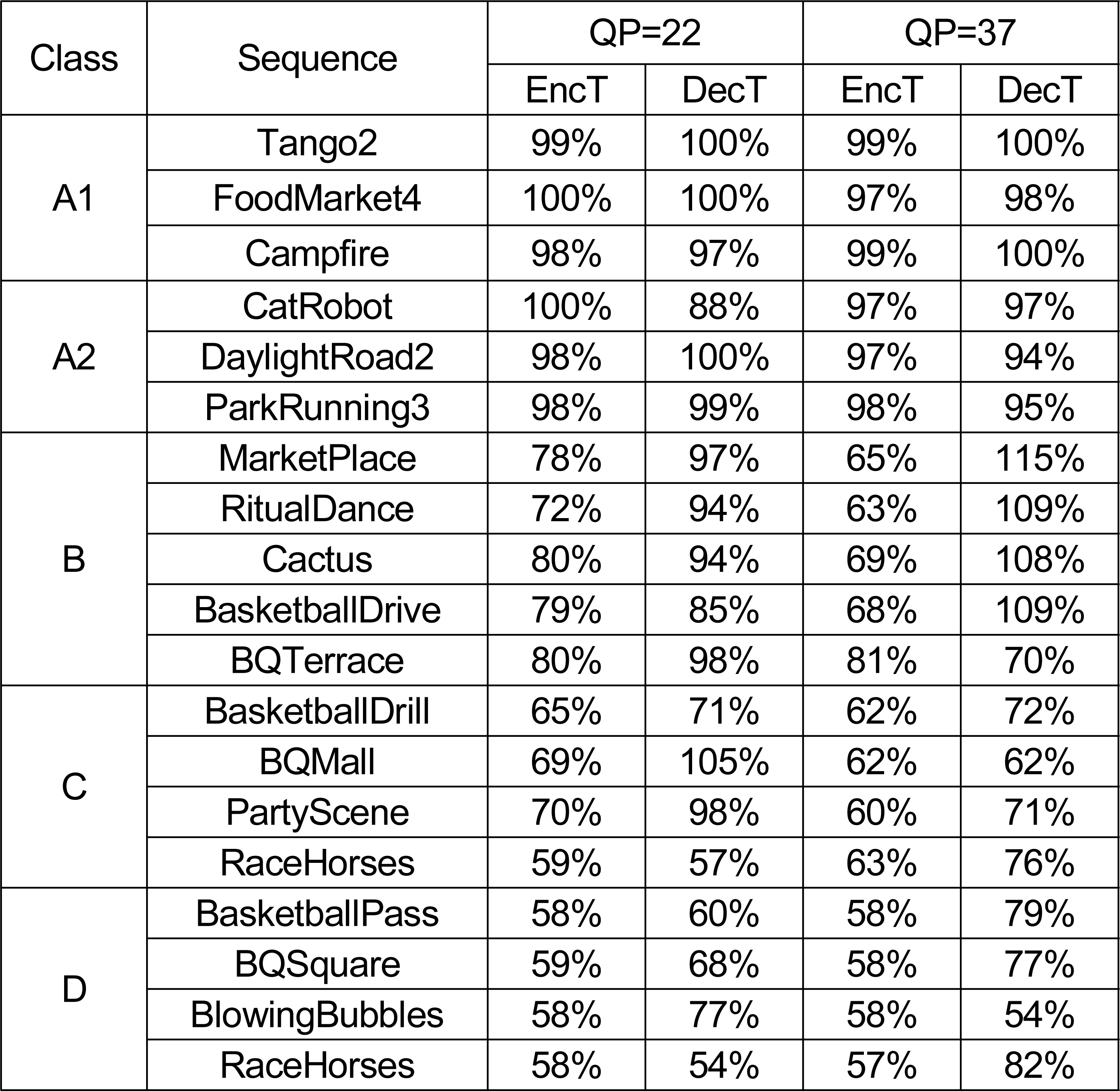
표 6은 QP가 22인 경우의 실험 결과와 QP가 37인 경우의 실험 결과를 비교한 표이다. 대부분의 영상에서 QP 값이 커질수록 부호화 시간이 감소하는 것을 확인할 수 있다. QP 값이 커질수록 양자화 과정에서 계수가 0이 될 확률이 증가한다. 따라서 역양자화 후 변환 블록 내의 0이 아닌 계수의 개수가 임곗값 이하일 확률이 증가한다.

표 6.

AI에서 QP에 따른 실험 결과Table 6. Experimental result per QP in AI

Ⅴ. 결 론

본 논문에서는 부호화기와 복호화기의 계산 복잡도를 낮추기 위해 변환의 선형성을 이용한 고속 역변환 방법을 제안한다. VVC에 새로운 기술들이 추가되면서 부호화기와 복호화기의 복잡도가 매우 증가하였다. 제안된 방법은 역변환에서의 곱셈 연산을 줄이기 위해 변환의 선형성을 이용한다. 제안된 역변환 방법은 VVC의 주변환에 적용되며, 기존의 고속 변환 방법과 달리 변환 기저의 종류와 관계없이 적용할 수 있다는 점에서 의의를 가진다. 제안된 방법은 기존 역변환 방법과의 곱셈 연산량 비교를 통해 선택적으로 수행되며, 추가적인 플래그 전송이 필요하지 않다. 실험은 VTM-8.2에서 진행되었으며, 부호화와 복호화 시간이 AI에서 각각 평균 26%, 15% RA에서 각각 평균 4%, 10% 감소하였다. 또한, 제안하는 고속 역변환 방법과 유사하게 이차변환에서 선형성과 변환의 크기, 이차변환이 적용되는 영역 내의 0이 아닌 계수의 개수를 이용하면 추가적인 복잡도 감소가 가능할 것으로 예상된다.

References

• Bross, B., Chen, J., Liu, S., Wang, Y. -K., Versatile Video Coding (Draft 10), JVET-S2001, (2020, Jul.).
• Sullivan, G. J., Ohm, J. -R., Han, W. -J., Wiegand, T., Overview of the High Efficiency Video Coding (HEVC) Standard, IEEE Transactions on Circuits and Systems for Video Technology, (2012, Dec.), 22(12), p1649-1668. [https://doi.org/10.1109/TCSVT.2012.2221191]
• Huang, Y. -W., et al. , Block Partitioning Structure in the VVC Standard, IEEE Transactions on Circuits and Systems for Video Technology, (2021, Oct.), 31(10), p3818-3833. [https://doi.org/10.1109/TCSVT.2021.3088134]
• Pfaff, J., et al. , Intra Prediction and Mode Coding in VVC, IEEE Transactions on Circuits and Systems for Video Technology, (2021, Oct.), 31(10), p3834-3847. [https://doi.org/10.1109/TCSVT.2021.3072430]
• Yang, H., et al. , Subblock-Based Motion Derivation and Inter Prediction Refinement in the Versatile Video Coding Standard, IEEE Transactions on Circuits and Systems for Video Technology, (2021, Oct.), 31(10), p3862-3877. [https://doi.org/10.1109/TCSVT.2021.3100744]
• Koo, M., Salehifar, M., Lim, J., Kim, S. -H., Low Frequency Non-Separable Transform (LFNST), 2019 Picture Coding Symposium (PCS), Ningbo, China, (2019), p1-5. [https://doi.org/10.1109/PCS48520.2019.8954507]
• Karczewicz, M., et al. , VVC In-Loop Filters, IEEE Transactions on Circuits and Systems for Video Technology, (2021, Oct.), 31(10), p3907-3925. [https://doi.org/10.1109/TCSVT.2021.3072297]
• Ahmed, N., Natarajan, T., Rao, K. R., Discrete Cosine Transform, IEEE Transactions on Computers, (1974, Jan.), C-23(1), p90-93. [https://doi.org/10.1109/T-C.1974.223784]
• Budagavi, M., Fuldseth, A., Bjøntegaard, G., Sze, V., Sadafale, M., Core Transform Design in the High Efficiency Video Coding (HEVC) Standard, IEEE Journal of Selected Topics in Signal Processing, (2013, Dec.), 7(6), p1029-1041. [https://doi.org/10.1109/JSTSP.2013.2270429]
• Zhao, X., et al. , Transform Coding in the VVC Standard, IEEE Transactions on Circuits and Systems for Video Technology, (2021, Oct.), 31(10), p3878-3890. [https://doi.org/10.1109/TCSVT.2021.3087706]
• Zhang, Z., et al. , Fast DST-VII/DCT-VIII With Dual Implementation Support for Versatile Video Coding, IEEE Transactions on Circuits and Systems for Video Technology, (2021, Jan.), 31(1), p355-371. [https://doi.org/10.1109/TCSVT.2020.2977118]
• Versatile Video Coding Test Model(VTM) 8.2, https://vcgit.hhi. fraunhofer.de/jvet/VVCSoftware_VTM/-/tree/VTM-8.2.
• Bossen, F., Boyce, J., Suehring, K., Li, X., Seregin, V, JVET Common Test Conditions and Software Reference Configurations for SDR Video, JVET-T2010, (2020, October).