전파 거리에 따른 위상 홀로그램 복원성능 분석 및 BL-ASM 개선 방안 연구
Copyright © 2023, The Korean Institute of Broadcast and Media Engineers
This is an Open-Access article distributed under the terms of the Creative Commons BY-NC-ND (http://creativecommons.org/licenses/by-nc-nd/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited and not altered.”
초록
물체의 진폭과 위상 정보가 free space에서 전달되는 과정을 디지털로 계산하여 기록한 것을 컴퓨터 생성 홀로그램(CGH)라고 한다. 이 CGH는 복소 홀로그램의 형태이지만, 이를 Phase-only 공간광 변조기(SLM)를 통해 디스플레이 하기 위해 위상 홀로그램의 형태로 변환하게 된다. 본 논문에서는, 물체의 진폭 정보를 위상 정보에 포함시키는 과정에서 DPAC 등 subsampling이 포함된 기법을 사용한다면 위상 홀로그램의 대역폭이 커지며, 그 결과로 복소 홀로그램 복원 시에는 없던 aliasing이 발생할 수 있음을 실험적으로 밝혔다. 또한, 이렇게 aliasing에 의해 복원성능이 저하되는 거리에서도 공간 주파수 범위를 제약하는 방법을 통해 좋은 화질의 위상 홀로그램 생성이 가능함을 보였다.
Abstract
A computer-generated hologram (CGH) is a digitally calculated and recorded hologram in which the amplitude and phase information of an image is transmitted in free space. The CGH is in the form of a complex hologram, but it is converted into a phase-only hologram to display through a phase-only spatial light modulator (SLM). In this paper, in the process of including the amplitude information of an object in the phase information, when a technique that includes subsampling such as DPAC is used, we showed experimentally that the bandwidth of the phase-only hologram increases, and as a result, aliasing that was not present in the complex hologram can occur. In addition, it was experimentally shown that it is possible to generate a high-quality phase-only hologram by restricting the spatial frequency range even at a distance where the numerical reconstruction performance is degraded by aliasing.
Keywords:
Computer-generated hologram, Propagation Distance, Double Phase Amplitude Coding, Deep LearningⅠ. 서 론
홀로그래피는 데니스 가보르(Dennis Gabor)에 의해 처음 제안된 기술로, 물체에서 반사된 물체광에 참조광이 간섭하여 생기는 간섭 패턴의 진폭과 위상을 특정 재료로 이루어진 매체에 기록하는 기술이다[1]. 컴퓨터 생성 홀로그램(Computer Generated Hologram, CGH)은 가상의 물체에서 나오는 물체광과 참조광이 만나 빛의 간섭될 때, 이 간섭 패턴이 전파되는 과정을 수치적으로 계산하여 기록한 것을 의미한다. CGH를 생성하면 공간광 변조기(Spatial Light Modulator, SLM)를 통해 디스플레이 할 수 있다. 다만, 하드웨어적인 한계로 CGH의 진폭과 위상을 모두 표현할 수 없어, Amplitude-only SLM을 통해 진폭만 디스플레이 하거나 Phase-only SLM을 통해 위상만 디스플레이 하기도 한다. 빛의 방향을 바꿔주는 Phase-only SLM과는 달리 빛의 밝기를 조절하는 Amplitude-only SLM을 사용하면 디스플레이 결과 전반적인 밝기가 낮아지는 단점이 있어, 참조광을 더욱 효율적으로 사용할 수 있는 Phase-only SLM을 주로 사용하고 있다[2]. 하지만 단순히 위상 정보만 디스플레이 하면 물체를 온전히 복원할 수 없으므로 물체의 진폭 정보를 위상에 담아 위상만으로도 물체를 잘 복원할 수 있도록 위상 홀로그램을 잘 생성하는 방법에 관한 연구가 활발히 이루어지고 있다[3].
홀로그램을 생성 및 복원하는 과정에서 물리적으로 빛이 회절하며 전파되는 과정을 계산하는데, 이때 각 스펙트럼 기반 회절 방정식(Angular Spectrum Method, ASM), 프레넬 회절 방정식(Fresnel diffraction), 프라운호퍼 회절 방정식(Fraunhofer diffraction)을 주로 사용한다. 위 방법들은 모두 원본 평면과 빛이 전파되는 평면이 평행할 때 사용하는 방법이며, 평행하게 있지 않더라도 위 세 방법을 확장된 방법으로 계산할 수 있다[4]. 다만, 프레넬 회절 방정식의 경우, 빛이 근축 근사(Paraxial approximation)를 하고 있을 때 사용하기 적절하며, 프라운호퍼 회절 방정식의 경우 빛이 전달되는 평면이 원본 평면으로부터 아주 멀리 떨어져 있을 때 사용하기에 적절하므로, 일반적으로 특별한 제약과 가정이 없는 한 ASM을 이용해 홀로그램을 생성 및 복원하게 된다.
ASM을 통해 물체를 특정 거리만큼 전파하면 물체의 진폭과 위상 정보를 담은 복소 홀로그램이 생성되고, 이를 다시 동일한 거리만큼 수치적으로 복원하면 기존의 물체를 잘 복원할 수 있다. 하지만 ASM뿐 아니라 앞서 소개한 모든 회절 방정식은 복소 홀로그램을 잘 생성하고 복원하기 위한 방정식으로, 위상 홀로그램을 생성하기 위해 물체의 진폭 정보를 위상에 담는 순간 동일한 거리에서 복원이 잘되지 않을 수 있다. 이 문제를 도식화하면 그림 1과 같다. 원본 이미지 X를 전파 거리 d로 ASM을 통해 복소 홀로그램, Aexp(iθ)를 생성한다. 이를 다시 수치적으로 복원한 결과를 Xcomplex라 하자. 생성된 복소 홀로그램에 다양한 방법을 적용하여 위상 홀로그램, exp(iθ')을 생성할 수 있다. 이를 수치적으로 복원한 결과를 Xpoh라 하면, Xcomplex에서는 복원 결과가 예상했던 대로 잘 나올 수 있지만 Xpoh에서는 예상하지 못한 복원 결과가 나올 수 있다.
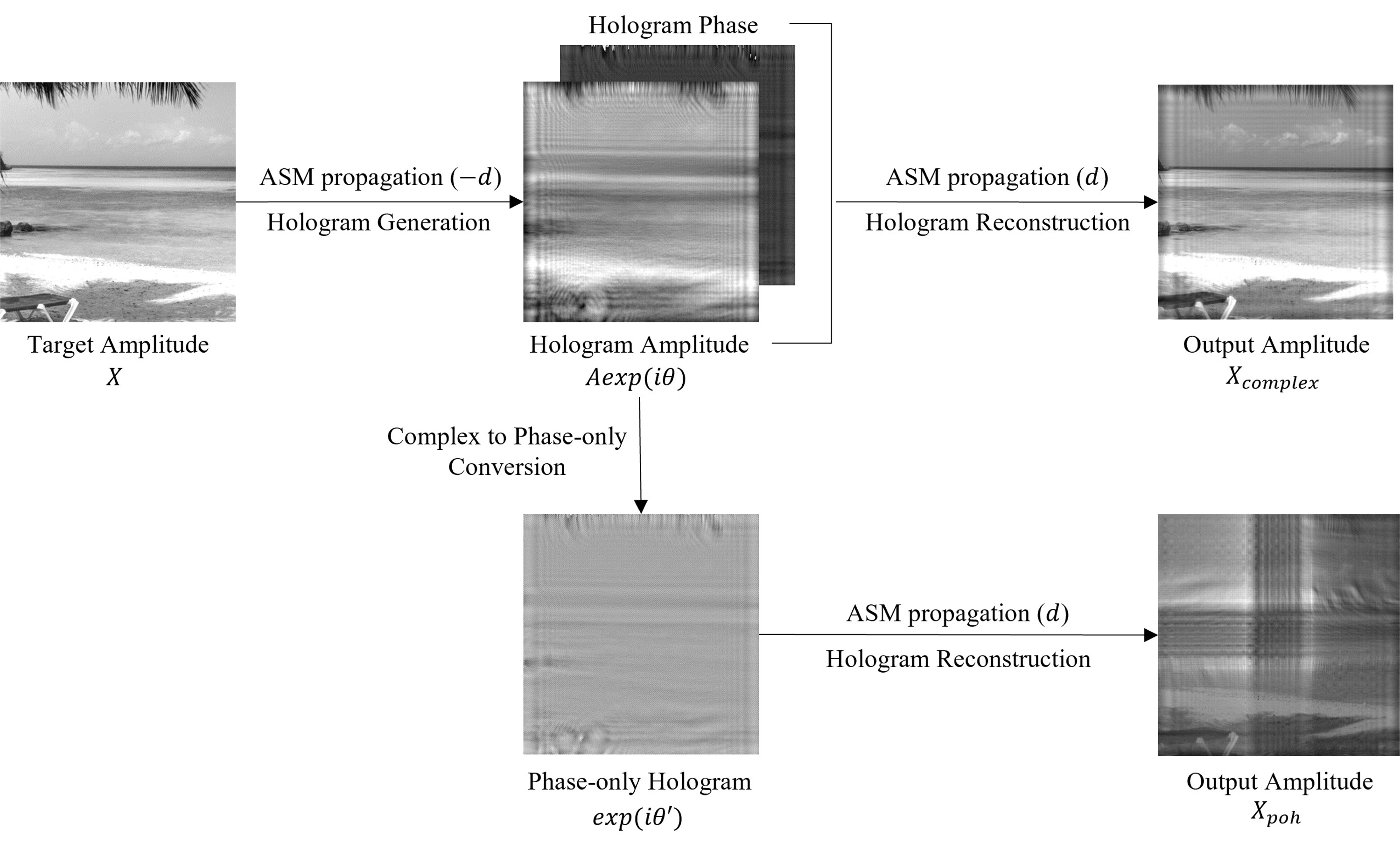
위상 홀로그램 생성 및 복원 시 적절한 전파 거리 세팅에 관한 문제Fig. 1. Problem about Propagation Distance Setting when Generating Phase-only Hologram
따라서 본 논문에서는, 위상 홀로그램의 복원성능이 어떤 경우에 저하되는지 실험적으로 밝히고, 이를 해결하기 위한 방법을 제시하고자 한다. 본 논문의 구성은 다음과 같다. 먼저 물체의 진폭과 위상 정보를 전달하는 ASM 방법에 대해 자세히 살펴보고, 이 방법으로 만들어진 복소 홀로그램을 위상 홀로그램으로 변환하는 다양한 방법들을 소개한다. 이후, 다양한 전파 거리에서 복소 홀로그램과 위상 홀로그램을 생성하고 다시 수치적으로 복원했을 때 결과를 살펴보며 어떤 차이가 있는지 분석한다. 본 논문의 실험 결과에 따르면, subsampling을 사용하는 위상 홀로그램 생성 기법을 사용했을 때, 고주파수 성분 증가에 따른 aliasing에 의해 복원성능이 저하됨을 알 수 있었고, 주파수 범위 제한을 통해 고주파수 성분을 제거했을 때 subsampling을 사용하는 위상 홀로그램 생성 방식에서도 복원성능을 향상시킬 수 있음을 보였다.
Ⅱ. 관련 연구
1. Band-Limited Angular Spectrum Method (BL-ASM)
이번 절에서는 aliasing 없이 ASM을 하기 위해 제안된 Band-limited Angular Spectrum Method (BL-ASM)[5] 방법에 대해 설명한다. Source wavefield g(x,y;z0)가 z0위치에 있을 때, 이를 초기값으로 하여 Helmholtz 2차 편미분 방정식을 풀면 d만큼 전파된 임의의 z 위치의 wavefield g(x,y;z)를 획득할 수 있다. 이 방법을 ASM이라고 하며, 다음과 같이 표현할 수 있다.
여기서 (u,v)는 각각 x축과 y축 방향으로의 공간 주파수를 나타내며, G(u,v;z0)는 g(x,y;z0)를 푸리에 변환한 결과로 이를 각 스펙트럼(Angular Spectrum)이라 한다, HAS는 ASM의 전달 함수를, • 은 두 피연산자의 곱 연산을 의미하며, F-1는 역푸리에 변환 연산을 나타낸다. λ를 파장의 길이라 하면, 전달 함수 HAS는 각 스펙트럼 회절 이론에 따라 다음과 같이 표현할 수 있다.
이때, 식(3)의 θ(u,v)를 각각 u,v에 대해 편미분하면 식 (4)와 식 (5)와 같이 u,v에 대한 지역 주파수를 구할 수 있다.
표본화 정리에 의하면, 주파수 도메인에서 표준화 간격의 역수가 해당 신호가 가질 수 있는 최대 주파수의 2배보다 클 때, aliasing이 발생하지 않을 수 있다. 하지만 식 (4)와 식 (5)를 보면 알 수 있듯, 전파 거리 d가 커질수록 전달 함수 HAS(u,v;d)가 가질 수 있는 지역 주파수의 최대 주파수가 커지면서, 대역폭이 증가하게 된다. 즉, 일정 거리를 넘어서게 되면 quadruple extension을 적용하더라도 여전히 aliasing이 발생할 수 있게 된다. 따라서 표본화 정리를 만족하도록 전파 거리를 제한하여 역 푸리에 변환 시 aliasing이 발생하지 않도록 할 수 있다.
1차원 신호를 ASM을 이용해 전파하는 문제로 단순화하면 지역 주파수는 다음과 같이 다시 정의할 수 있다.
표본화 정리 조건을 전파 거리 d에 대해서 정리하면 다음과 같다.
여기서 Δu는 u축으로의 표본화 간격을 의미한다. 즉, dmax(u)의해, 공간 주파수 u가 커질수록 aliasing이 발생하지 않도록 최대로 전파할 수 있는 거리는 점점 작아지게 된다. 원본 신호가 가질 수 있는 최대 공간 주파수 umax는 원본 신호의 표본화 간격 Δx 및 표본화 개수 N에 의해 다음과 같이 결정된다.
식 (10)의 최대 공간 주파수 umax를 식 (8)의 최대 전파 거리 계산식 dmax(u)에 대입하면 해당 신호를 온전히 전파할 수 있는 최대 전파 거리를 계산할 수 있다.
d≤dmax(umax)의 경우, aliasing 없이 온전한 신호를 전파할 수 있지만, d>dmax(umax)의 경우, 표본화 조건을 만족하지 못해 aliasing이 발생한다.
또한, 식 (7)과 같은 표본화 정리 조건에서 전파 거리 d가 아닌 전달 함수의 주파수 범위를 제한할 수 있다. 위 수식을 공간 주파수 u에 따라 정리하면 다음과 같다.
즉, ubl(d)에 의해 전파 거리 d가 커질수록, aliasing 없이 전파할 수 있는 공간 주파수 크기는 점점 작아지게 된다. 다만, 식 (12)를 따라 공간 주파수 u가 umax(d)보다 작도록 제한하면, 전파 거리 d를 키워도 aliasing 없이 신호를 전파할 수 있는데, 이렇게 공간 주파수의 범위를 제한하는 방법을 Band-limited method라고 한다.
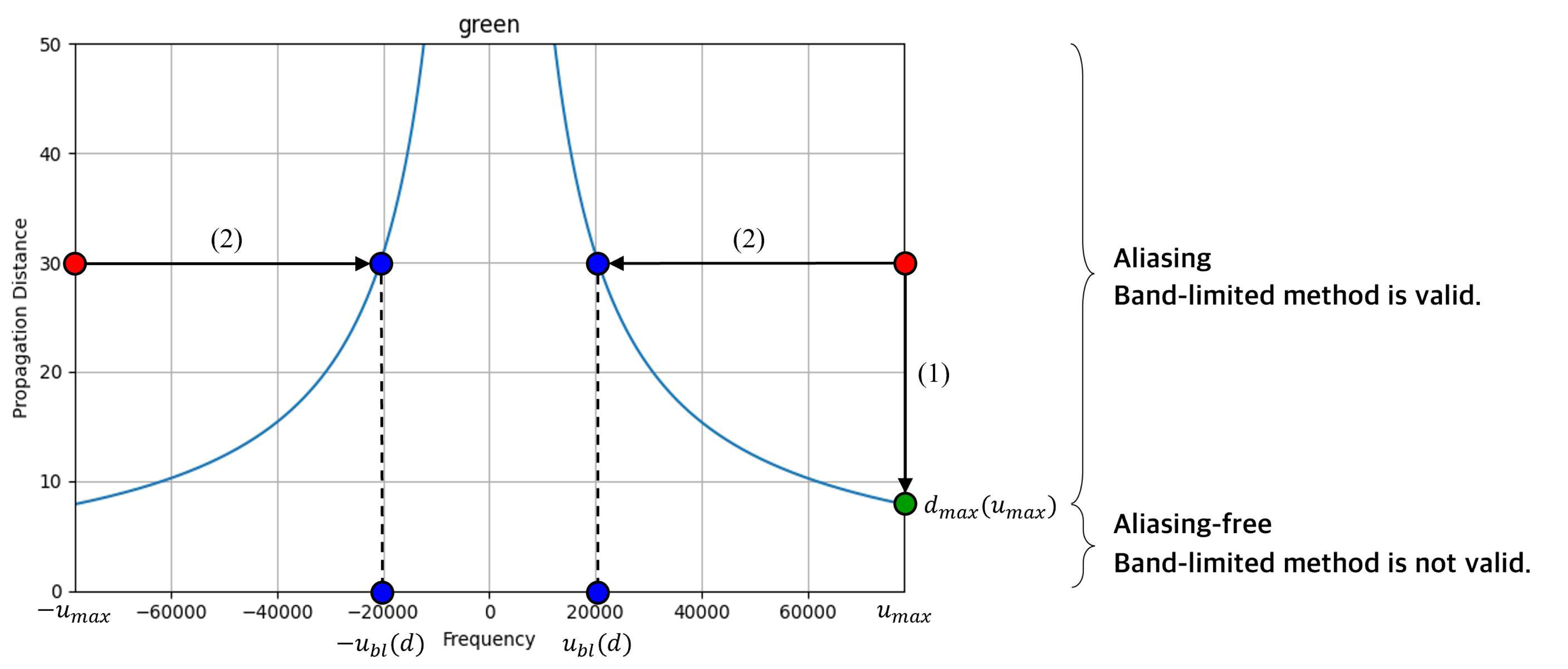
그림 2에서 x축은 전파하고자 하는 신호의 공간 주파수 범위를 나타내고, y축은 전파 거리를 나타낸다. x축과 y축으로 이루어진 좌표계에 그려진 그래프는 표본화 간격은 6.4㎛, 표본화 개수는 1,024, 단파장의 길이는 532㎚(Green)일 때의 dmax(u)혹은 ubl(d)를 나타낸다. 그림 2는 원본 신호를 30㎝로 전파한다고 가정했을 때, 식 (8)과 식 (12)로 aliasing 없이 전파할 수 있는 2가지 방법을 나타낸 것이다. 그림 2의 (1)은 식 (8)의 방법을 나타낸 것으로, 원본 신호 전체를 보존하며 전파하되, 30㎝가 아닌 dmax(umax)보다 짧은 거리로 전파한다. 그림 2의 (2)는 식 (12) 의 방법을 나타낸 것으로, 30㎝로 전파하되, aliasing이 나타날 수 있는 |ubl(d)|보다 큰 고주파수 영역을 제한하여, 그보다 작은 주파수를 가진 영역만 전파한다. 전파 거리를 제한하는 (1)의 방법을 사용하면 원하는 거리만큼 신호를 주고 받을 수 없으므로, 일반적으로 원본 신호의 정보를 조금 손실하더라도 원하는 거리로 전파할 수 있는 (2)의 방법을 사용한다.
그림 2의 (2)번 방법을 앞서 빛을 전파하는 각 스펙트럼 방법과 결합하여 aliasing 없이 전파할 수 있도록 확장하였을 때, 이를 Band-limited Angular Spectrum Method (BL-ASM)[5]이라고 한다. 앞서 정의한 uBL과 마찬가지로 공간 주파수 v축에 대해서도 vBL을 정의하여 기존의 ASM, 수식 (1)을 이산적으로 표현하면 다음과 같이 확장할 수 있다.
여기서 , [m,n], [p,q]는 기존의 연속 도메인 (x,y), (u,v) 를 각각 표본화 한 것이며, Δu, Δv는 각각 u축과 v축의 표본화 간격을 의미한다. rect(•)는 구형함수를 나타내며, 기존의 ASM 전달 함수 HAS에서 표본화 정리 조건에 충족하는 공간 주파수만 포함될 수 있도록 구형함수를 통해 제한한 전달 함수가 HBL-ASM이다. BL-ASM을 사용하면 dmax(umax)보다 큰 전파 거리에서도 aliasing이 발생할 수 있는 공간 주파수 영역을 제한하면서 원본 신호를 aliasing 없이 전파할 수 있다.
결과적으로, aliasing이 발생하지 않도록 2차원 신호를 d만큼 전파하는 방법으로 식 (11)에 의해 구한 최대 전파 거리 dmax(umax)보다 작은 전파 거리 범위 안에서 source wavefield를 전파하는 방법이 있고, 전파 거리에 상관없이 식 (12)에 따라 aliasing이 나타날 수 있는 공간 주파수 범위를 제한하여 전파하는 방법이 있다. 다만, 최대 전파 거리 dmax(umax)를 제한하면 원하는 거리만큼 홀로그램을 생성 및 복원할 수 없으므로, 최대 전파 거리 이상의 거리에서는 공간 주파수 범위를 제한하는 BL-ASM을 사용하게 된다.
2. Methods of Phase-only Hologram Generation
BL-ASM 방법을 이용해 물체의 진폭과 위상 정보를 전파하게 되는데, 전파된 진폭과 위상 정보를 모두 기록한 것을 복소 홀로그램이라고 한다. 이를 위상 홀로그램으로 만드는 가장 단순한 방법은 진폭을 버리고 위상만 기록하는 것이다. 일반적으로 위상에는 물체의 경계선과 같은 고주파수 성분들을 가지는 경향이 있어, 얇은 선으로 이루어진 텍스트나 심볼로 위상 홀로그램을 만들거나 간단히 위상 홀로그램 영상을 만들어 테스트하고 싶을 때, 진폭 정보를 버림으로써 빠르고 효율적으로 위상 홀로그램을 생성할 수 있다[6]. 하지만 일반적으로 자연 이미지에는 고주파수 성분보다 저주파수 성분이 많으므로 단순히 진폭을 버리는 방법을 선택한다면 많은 정보를 잃을 수 있어 자주 사용되는 방법은 아니다. 따라서 물체의 진폭 정보를 위상에 담을 수 있도록 다양한 방법을 사용하게 되는데, 대표적으로 이중 위상 표현[7]과 이를 활용한 Double Phase Amplitude Coding (DPAC)[6], 반복 최적화 기법인 GS-algorithm[8]과 신경망을 활용하는 방법[9-12] 등이 있다.
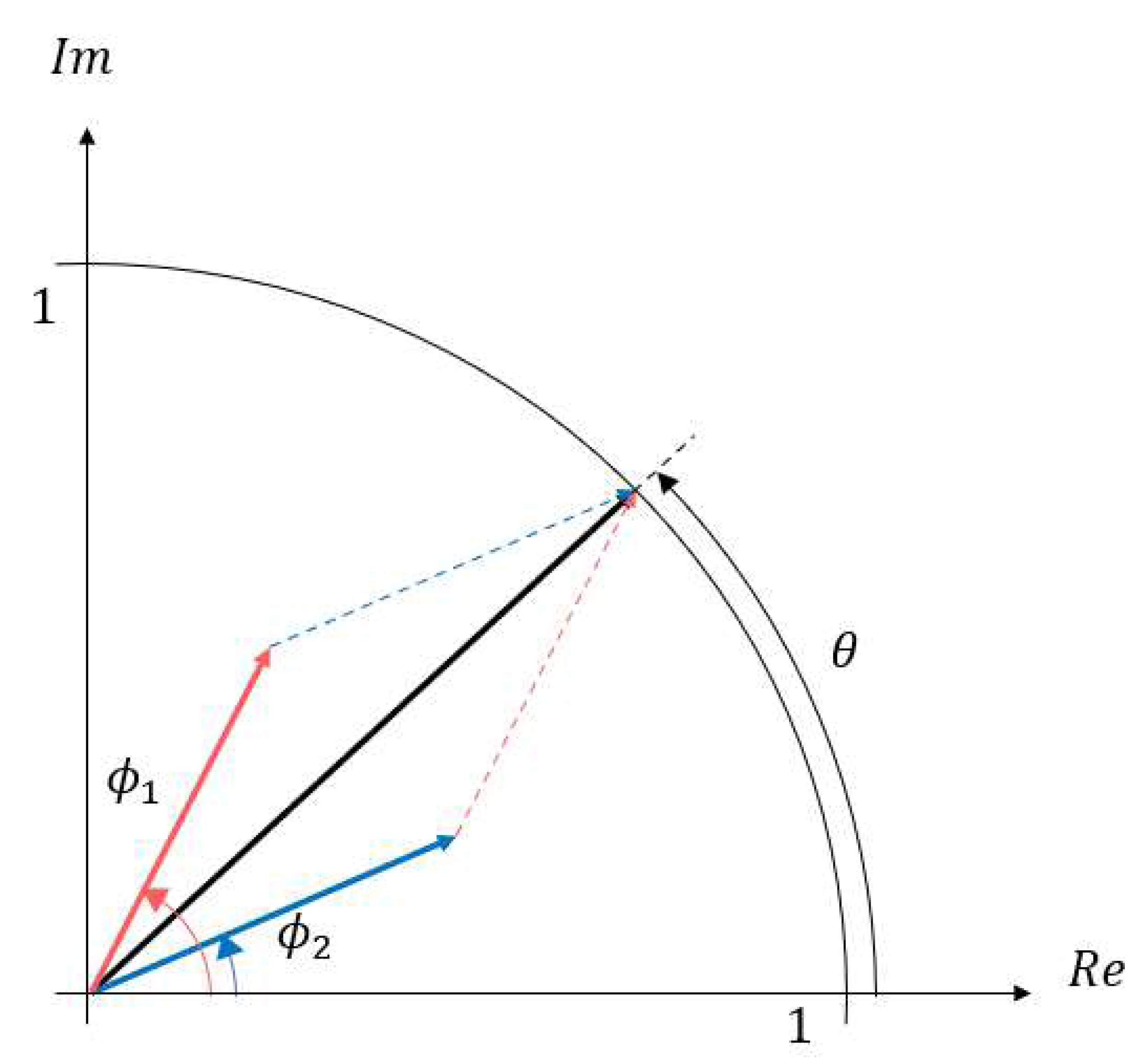
첫 번째로, 이중 위상 표현[7]은 복소 홀로그램을 2개의 위상으로 손실 없이 변환하는 방법이며, 다음과 같은 수식으로 정리할 수 있다.
복소 홀로그램 H의 진폭 A가 [0,1]의 범위를 가지고 있다면, 진폭이 0.5로 상수이고 위상이 각각 ϕ1,ϕ2인 위상 홀로그램을 생성할 수 있다. 이렇게 생성된 두 개의 위상 홀로그램을 동시에 디스플레이 할 수 있으면, 기존 복소 홀로그램의 진폭과 위상 정보를 모두 활용하기 때문에 복소 홀로그램과 동일한 화질의 홀로그램을 복원할 수 있다.
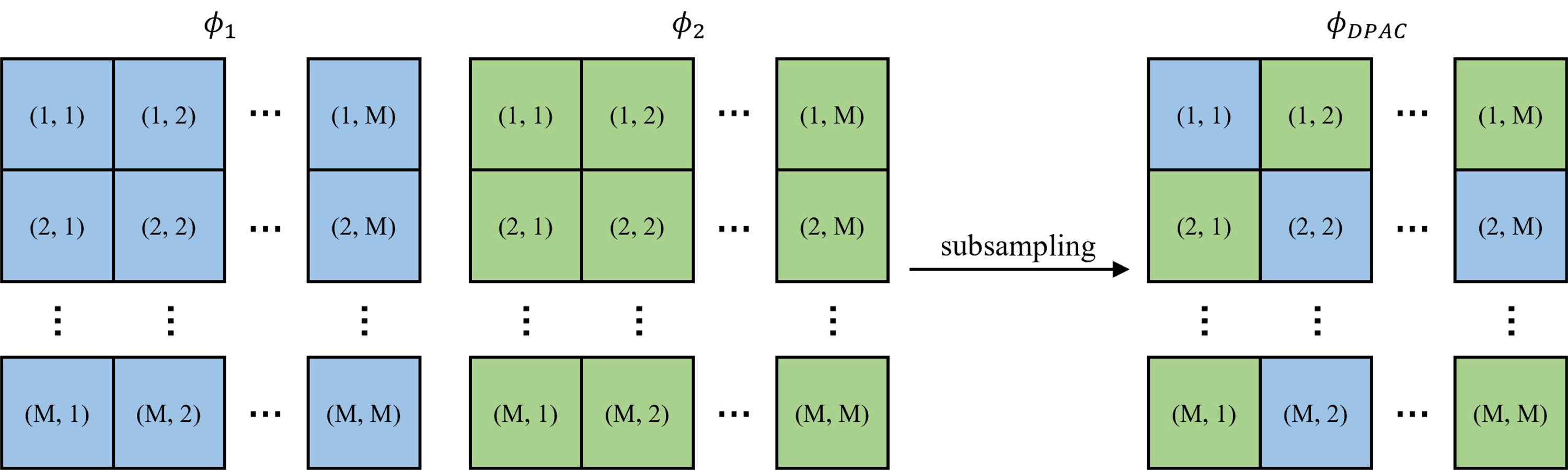
하지만 아직 두 개의 위상 홀로그램을 동시에 디스플레이 할 수 있는 기술이 없으므로, 각각의 위상을 바둑판 모양처럼 배치하여 하나의 위상 홀로그램을 생성하는 방법을 사용한다. 자세한 방법은 그림 4과 같다. 첫 번째 위상을 ϕ1, 두 번째 위상을 ϕ2라고 하면, (1,1) 좌표에는 ϕ1, (1,2) 좌표에는 ϕ2을 위치시킨다. 이렇게 ϕ1,ϕ2를 번갈아 가면서 배치하면 ϕDPAC위상을 얻게 되며, 이와 같은 방법을 Double Phase Amplitude Coding (DPAC)[6]이라 한다. 다만, 이중 위상이 각각 절반씩 표본화되기 때문에 정보 손실이 발생한다.
위상 홀로그램을 생성할 때 주로 사용하는 방법으로 반복 최적화 방법이 있다. 대표적인 반복 최적화 방법으로는 Gerchberg-Saxton algorithm (GS algorithm)[8]이 있으며, Iterative Fourier Transform Algorithm (IFTA)라 하기도 한다. GS algorithm은 무작위로 생성된 위상 홀로그램을 복원했을 때 원본 이미지의 진폭을 가지도록 제한한 후, 이를 다시 위상 홀로그램을 만드는 과정을 반복하는 알고리즘으로, 원본 물체의 진폭 정보가 위상에 포함되도록 만든다. 단순히 진폭을 무시하는 방법보다 위상 홀로그램을 안정적으로 생성할 수 있지만, 좋은 위상 홀로그램을 생성하기까지 많은 반복 횟수를 거쳐야 하므로 오랜 시간이 걸린다는 단점이 있다.
이 문제를 해결하기 위해 최근에는 딥러닝을 이용해 위상 홀로그램을 생성하는 방법에 관한 연구[9-12]가 활발히 이루어지고 있다. 잘 학습된 위상 홀로그램 생성 네트워크를 활용하면 물체의 진폭과 위상 정보가 위상 홀로그램에 효율적으로 담을 수 있으며, 좋은 홀로그램을 빠르게 생성할 수 있다. 대표적으로 [9]에서는 U-net을 기반으로 랜덤하게 생성한 프레넬 회절 패턴을 학습하는 방법을 통해 위상 홀로그램을 한 번에 생성하는 방법을 제안하였으며, [10]에서는 원본 이미지와 네트워크를 통해 생성된 위상 홀로그램을 복원한 결과의 차이를 학습하여 3D 홀로그램을 생성하는 DeepCGH를 제안하기도 하였다. 이후 많은 연구가 이루어지면서 [11]에서는 원본 이미지에서 네트워크를 통해 초기 위상을 먼저 생성한 후, 이를 전파한 뒤 또 다른 네트워크를 통해 위상 홀로그램을 생성하는 HoloNet을 제안하였으며, [12]에서는 자체적으로 생성한 고해상도 위상 홀로그램 데이터 MIT-CGH-4K를 통해 실시간으로 사실적인 3D 홀로그램을 생성하는 Tensor Holography를 제안하였다. 본 논문에서는 [11]에서 제안한 학습 전략을 활용해 U-net을 기반으로 위상 홀로그램 생성 네트워크를 학습하였다.
Ⅲ. 실험 및 결과
1. 복소 홀로그램 생성 실험 (Lossless)
위상 홀로그램을 생성을 위한 적절한 전파 거리에 대해 고찰하기 전, BL-ASM으로 생성한 복소 홀로그램이 이론적으로 문제가 없는지 실험적으로 검증할 필요가 있다. BL-ASM의 수식에 따르면 전달 함수 HBL-ASM에 의해 전파 거리 d가 커질수록 wavefield의 위상이 변형이 일어나며, 표본화 정리를 만족하기 위한 대역폭의 제한으로 실제 물체의 진폭 및 위상 정보가 온전히 전달되지 않을 수 있다. 즉, 전파 거리 d가 커질수록 복소 홀로그램을 복원한 이미지의 화질이 점점 낮아질 것으로 예상된다.
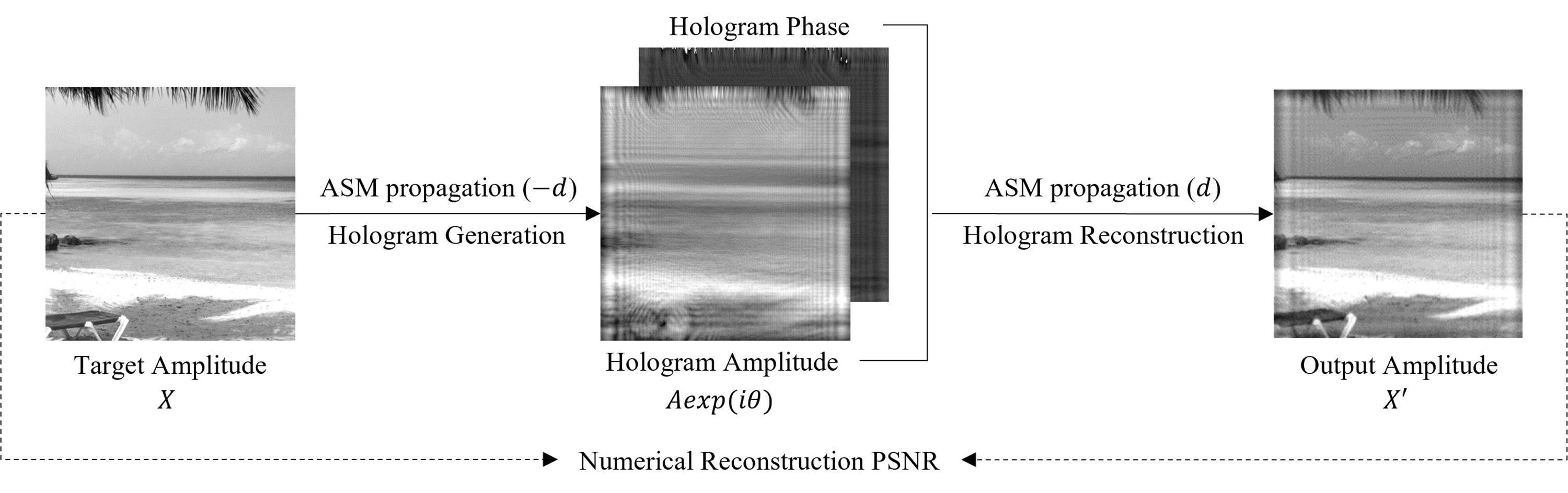
실험은 그림 5와 같은 방법으로 진행된다. 원본 이미지 X를 BL-ASM으로 -d만큼 전파하여 복소 홀로그램, Aexp(iθ)를 생성한다. 생성된 복소 홀로그램을 이전과 반대 방향으로 d만큼 전파하여 수치적으로 복원한 결과 X'을 생성한다. 이때, 원본 이미지 X와 홀로그램을 복원한 결과 X'를 이용해 Peak Signal-Noise Ratio (PSNR)을 계산 한다. 추가로, BL-ASM을 통해 생성된 CGH의 진폭을 [0, 1]로 제한하고 이중 위상 표현에 따라 두 개의 위상으로 분리한 후, 수치적으로 복원한 결과의 평균을 계산하여 원본 이미지와의 PSNR을 통해 복원성능을 비교하였다.
공정한 비교 실험을 위해 데이터는 DIV2K[13] validation dataset을 각 이미지 당 512×512크기로 랜덤하게 3장씩 잘라내어 총 300장의 이미지를 사용하였고, 푸리에 변환 과정에서 aliasing이 발생하지 않도록 quadruple extension을 적용하여 전파하였다. 표본화 간격은 6.4μm, 단파장의 길이는 로 고정하였다. 반면, 전파 거리는 1㎝~20㎝ 사이 거리를 기준으로 다양하게 변화시켜가며 실험을 진행하였다.
복소 홀로그램을 생성 및 복원한 실험 결과는 표 1과 같다. 앞서 예상했던 대로 전파 거리가 가장 짧은 1㎝일 때 원본 이미지와 가장 비슷한 복원성능을 보여주었으며, d가 커질수록 복원성능이 떨어지는 것을 확인할 수 있다. 또한, 푸리에 변환 연산은 선형적 연산이므로, 복소 홀로그램을 이중 위상 표현으로 두 개의 위상 홀로그램을 만들고 이를 각각 복원하여 평균을 낸 결과와 복소 홀로그램을 복원한 결과가 동일하게 나타나는 것을 확인할 수 있었다. 이는 앞서 예상한 결과와 일치하는 결과로 BL-ASM으로 복소 홀로그램을 생성하고 복원하는 데 이론적으로 문제가 없음을 확인할 수 있었다.
2. 위상 홀로그램 생성 실험 (Lossy)
복소 홀로그램의 경우에는 전파 거리 d가 커짐에 따라 복원성능이 떨어지는 모습을 보인다. 이 복소 홀로그램을 위상 홀로그램으로 변환하면 물체가 가지고 있는 정보 일부를 잃게 되므로, 동일한 d에서 복소 홀로그램에 비해 위상 홀로그램의 복원성능은 떨어지는데, 이때 정보의 손실이 얼마나 발생했는지에 따라 전파 거리 d에 따른 복원성능이 복소 홀로그램의 경우와 달라질 수 있다. 따라서, 본 절에서는 위상 홀로그램의 경우에 d에 따른 복원성능을 실험적으로 확인해보고자 한다.
실험은 그림 6과 같은 방법으로 진행된다. 원본 이미지 X를 BL-ASM으로 -d만큼 전파하여 복소 홀로그램, Aexp(iθ)를 생성하면, amplitude discard method, DPAC, GS algorithm을 이용해 위상 홀로그램 exp(iθ')을 생성한다. 위상 홀로그램을 이전과 반대 방향으로 d만큼 전파하여 수치적으로 복원한 결과 X'을 생성한 후, 원본 이미지 X와 PSNR을 통해 복원성능을 비교한다. 이때, 사용한 실험 조건은 앞서 복소 홀로그램의 복원성능 비교 실험과 같도록 설정하였으며, 다만 GS algorithm은 총 500번 반복하여 위상 홀로그램을 생성하였다.
위상 홀로그램 생성 및 복원 실험 결과는 표 2와 같다. 단순히 진폭 정보를 무시하는 방법을 사용하면 원본 이미지에 존재하는 많은 정보를 잃어버리기 때문에, 복소 홀로그램에 비해 복원성능이 많이 떨어지는 모습을 확인할 수 있었다. GS algorithm으로 생성된 위상 홀로그램의 경우, 단순히 진폭 정보를 무시했을 때보다 좋은 화질의 위상 홀로그램을 안정적으로 생성할 수 있었으며, 전파 거리에 따른 위상 홀로그램 복원성능을 비교했을 때 복소 홀로그램과 비슷한 양상을 띠는 것을 확인할 수 있었다. 다만, 그림 8에서처럼 GS algorithm으로 생성된 위상 홀로그램은 복원했을 때 전반적으로 잡음이 많이 섞인 모습을 확인할 수 있었다.

Phase-only Hologram 복원 화질 평가 결과Table. 2. Numerical Reconstruction PSNR Result of Phase-only Hologram
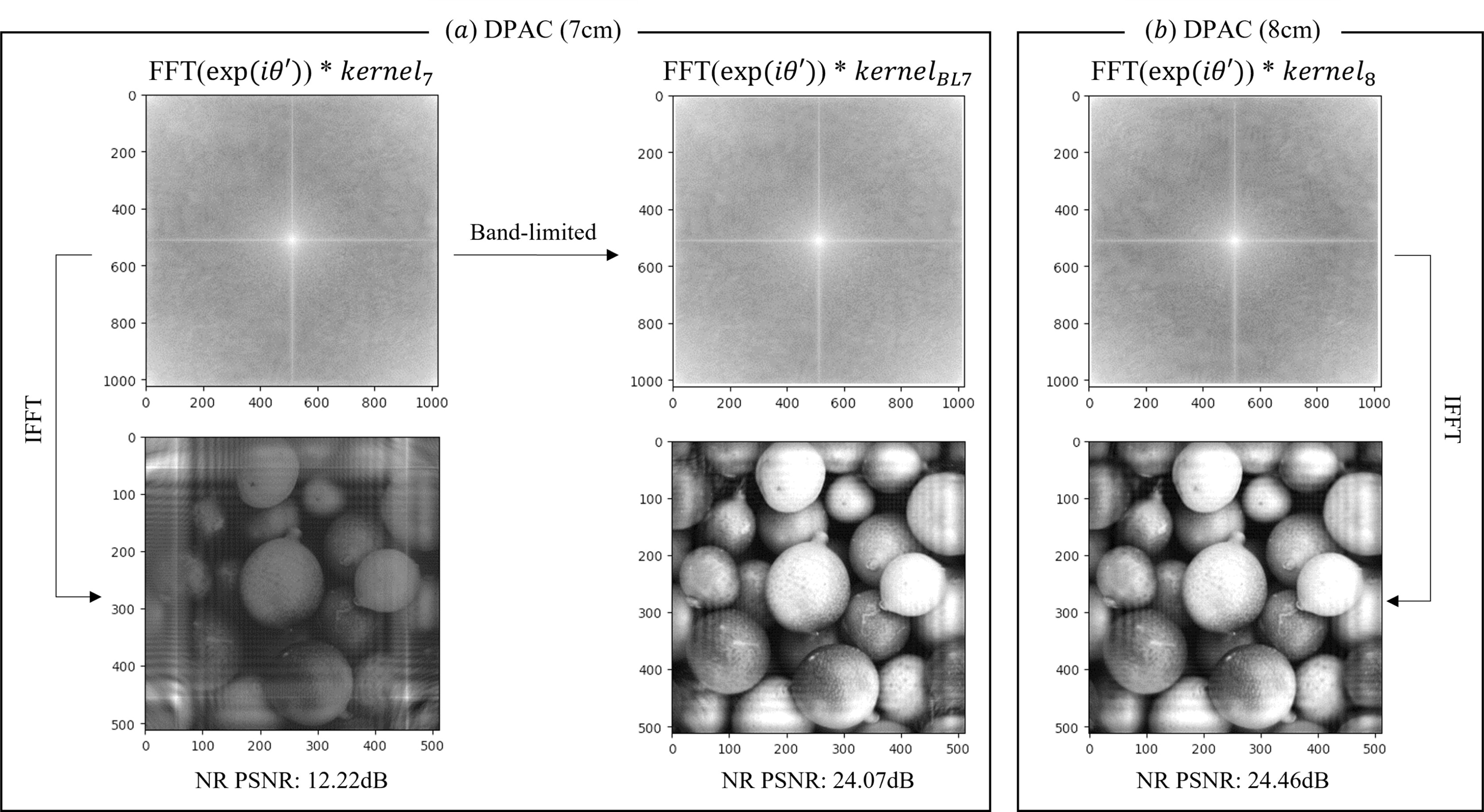
문제는 DPAC을 통해 만들어진 위상 홀로그램을 복원할 때이다. d가 커질수록 복원성능이 떨어질 것이라는 예상과는 달리, d가 작을 때는 진폭 정보를 제한한 결과보다 복원성능이 더 안 좋은 모습을 보이다가 d가 7㎝에서 8㎝로 넘어가는 순간 복원성능이 갑자기 좋아지는 모습을 확인할 수 있었다. 그림 7을 통해 DPAC로 생성된 위상 홀로그램을 복원한 결과를 확인하면, 8㎝일 때는 원본 이미지와 유사하게 위상 홀로그램이 잘 복원되었지만, 7㎝일 때는 모서리에 노이즈가 섞이면서 원본 이미지와 전혀 다른 모습으로 복원되었음을 확인할 수 있었다. 즉, 복소 홀로그램과 동일한 방법으로 위상 홀로그램을 복원하더라도 전파 거리에 따른 결과가 완전히 다른 양상을 보이는 경우가 존재하고 있었다.
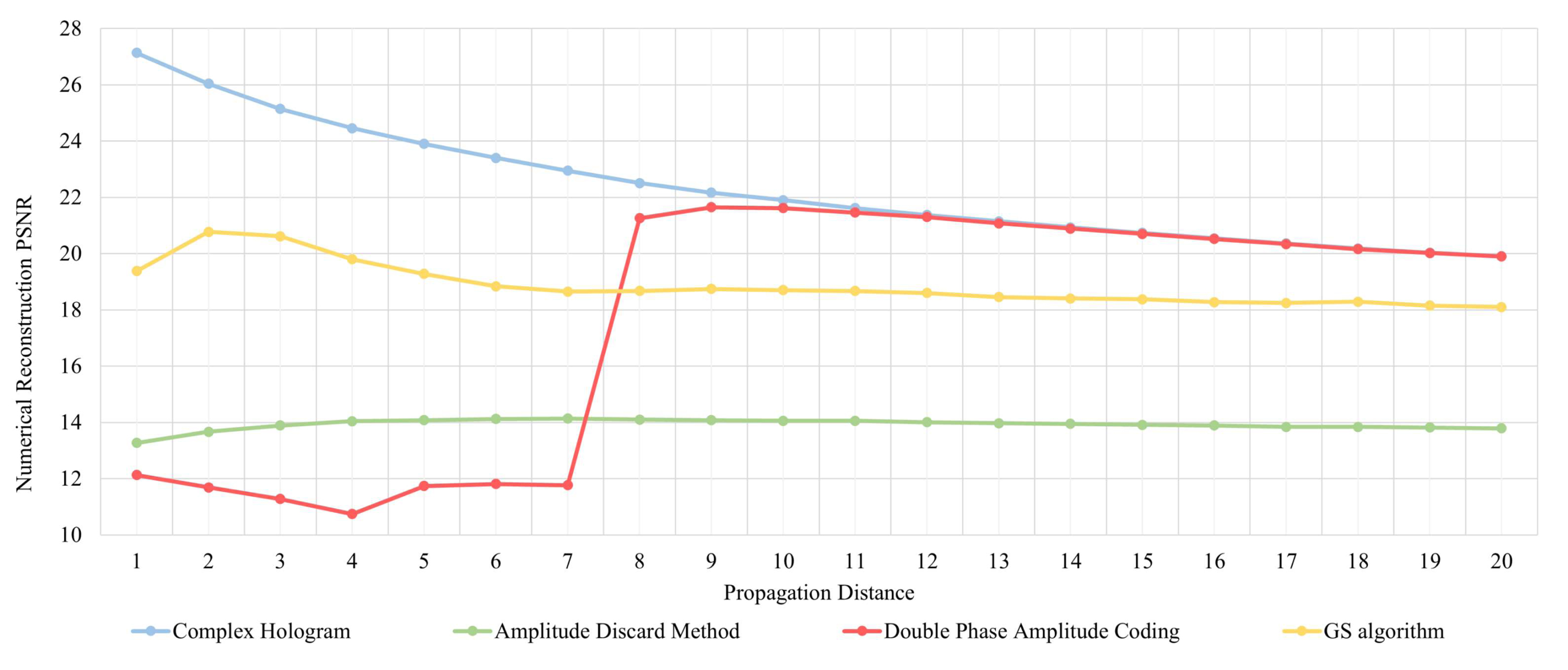
전파 거리에 따른 컴퓨터 생성 홀로그램 수치적 복원 화질 성능 비교Fig. 7. Comparison of Numerical Reconstruction PSNR with respect to Propagation Distance
Ⅳ. 분석 및 개선
1. Case Study
DPAC로 위상 홀로그램을 생성하는 방법은 총 3단계로 나누어 생각해 볼 수 있다. 먼저, 원본 이미지를 BL-ASM을 통해 전파하여 복소 홀로그램을 생성한다. 그 다음, 이중 위상 표현을 통해 2개의 위상 홀로그램으로 변환한다. 이후, 하나의 위상 홀로그램으로 만들기 위해 2개의 위상을 checkerboard pattern으로 subsampling 한다. 하지만 표 1에서 보았듯 복소 홀로그램을 생성하는 과정은 물론, 이중 위상 표현으로 얻은 2개의 위상 홀로그램을 복원하는 과정에서도 어떤 문제가 발생하지 않았다. 즉, subsampling을 통해 하나의 위상 홀로그램을 만드는 단계에서 문제가 발생했음을 알 수 있으며, 특히 subsampling 하는 과정에서 aliasing이 발생해 고주파수 성분이 많아져 복소 홀로그램이나 이중 위상으로 표현된 위상 홀로그램을 복원할 때 사용하는 전달 함수보다 대역폭이 커졌을 가능성이 있다.
표본화 정리에 따라 ASM을 통해 wavefield를 전파할 때 aliasing이 발생하지 않게 하려면, 식 (8)에 따라 최대 전파 거리 제한을 만족하거나 식 (12)에 따라 공간 주파수 범위를 제한할 수 있다. 앞선 실험 조건에 따라 최대 전파 거리 dmax(umax)를 계산하면 7.877218㎝가 되는데, 이는 일반적인 ASM을 이용해 7㎝로 전파하면 aliasing이 발생하지 않지만, 8㎝로 전파하면 aliasing이 발생함을 의미한다. 따라서 8㎝를 넘어가는 전파 거리에서도 aliasing이 발생하지 않도록 공간 주파수 범위를 제한하면서 전파하게 되는데, 이때 고주파수 성분들이 제거된다. 즉, 전파 거리 7㎝에서 DPAC로 만든 위상 홀로그램을 복원하는 경우, BL-ASM 방법을 사용해 전파했음에도 불구하고 고주파수 성분이 제한되지 않아 subsampling에 의해 발생한 aliasing이 문제가 되었다고 볼 수 있다.
위 가설을 검증하기 위해, 하나의 데이터에서 복소 홀로그램과 DPAC를 통해 생성한 위상 홀로그램을 푸리에 변환하여 주파수 도메인에서 비교하였다. 결과는 그림 9과 같다. 그림 9의 (a)는 DPAC로 만든 위상 홀로그램을 푸리에 변환한 결과이고, 그림 9의 (b)는 복소 홀로그램을 푸리에 변환한 결과이다. 전파 거리가 7㎝일 때, DPAC로 만든 위상 홀로그램을 푸리에 변환한 결과는 복소 홀로그램을 푸리에 변환한 경우와 달리 고주파수 성분이 상승한 모습을 확인할 수 있었다. 이를 통해 DPAC의 subsampling 과정이 위상 홀로그램을 복원하는 과정에서 고주파수 성분을 추가로 가지도록 만들었음을 알 수 있다.
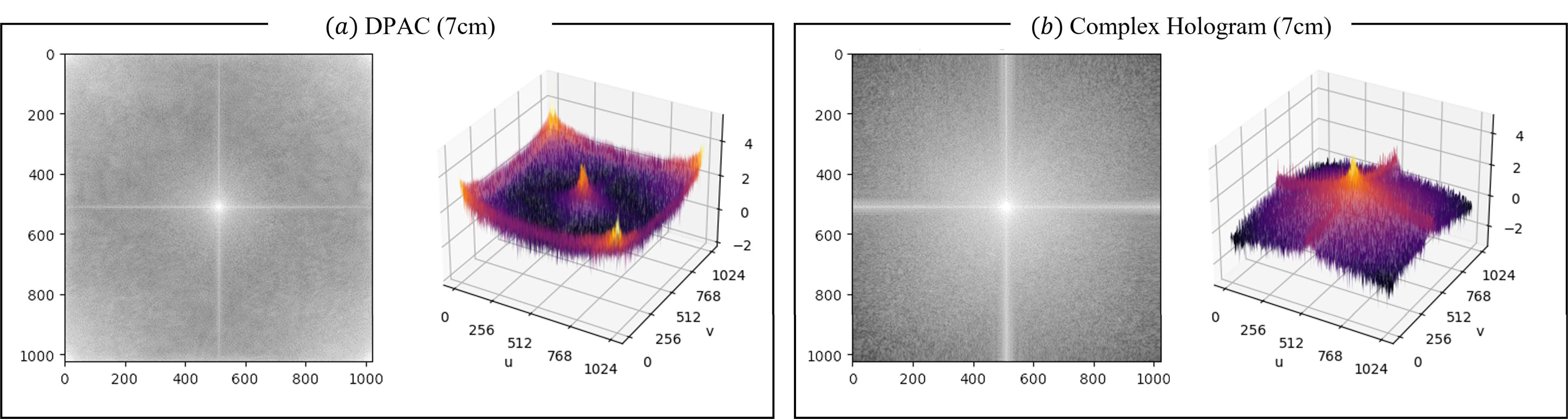
DPAC으로 생성한 위상 홀로그램 (a) / 복소 홀로그램 (b) 푸리에 변환 연산 결과Fig. 9. Result of Fourier Transform Operation (Phase-only Hologram generated with DPAC (a) / Complex Hologram (b))
이후, 그림 10의 (a)와 같이 전파 거리 8㎝에서 aliasing이 발생하지 않도록 공간 주파수 범위를 제한하는 만큼, 동일하게 전파 거리 7㎝에서도 제한을 걸어 복원해보았다. 공간 주파수 범위에 제한을 걸지 않았을 경우 복원성능이 12.22dB으로, 매우 낮은 복원성능을 보여주었지만, 제한을 걸어 복원했을 경우 24.07dB로, 복원성능이 거의 2배 가까이 상승한 것을 확인할 수 있었다. 즉, 적어도 전파 거리가 7㎝인 경우, 고주파수 성분을 일부 제한하여 DPAC을 통해 얻어진 aliasing을 제거하면 위상 홀로그램의 복원성능이 향상함을 알 수 있었다.
2. Subsampling을 고려한 BL-ASM 방법의 확장
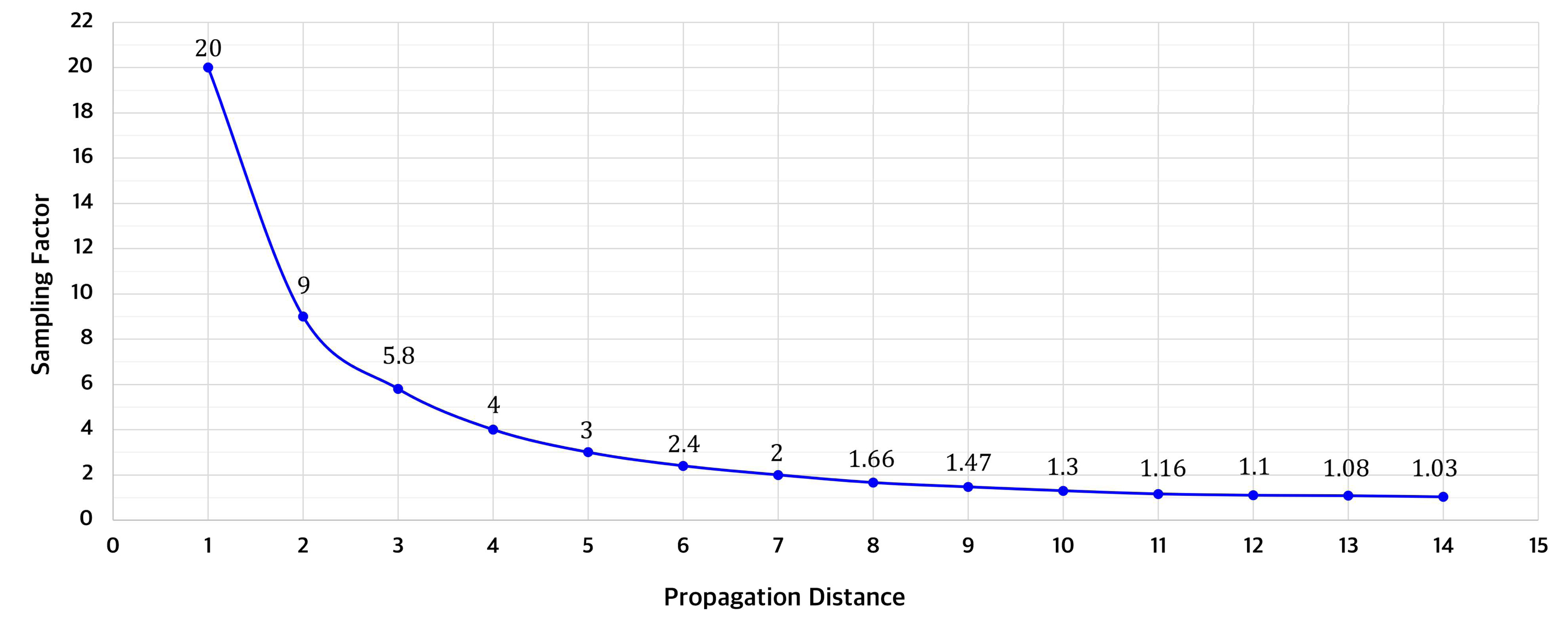
본 논문에서는 상기한 실험 결과를 통해 얻은 아이디어를 확장하여 기존의 BL-ASM이 적용되지 않던 거리에서도 대역 제한을 추가적으로 적용함으로써 DPAC의 subsampling에 의해 발생한 aliasing을 효과적으로 제거할 수 있음을 보이고자 한다. Subsampling 적용 전의 표본화 간격을 식 (9)에서와 마찬가지로 Δu라 하면, subsampling에 의해 더 늘어난 표본화 간격 Δu'은 sampling factor α을 이용하여 식 (19)와 같이 나타낼 수 있다. 이때, sampling factor α는 DPAC에 의해 기존의 표본화 간격 Δu가 얼마나 늘어나는 지를 모형화하기 위해 본 논문에서 도입한 파라미터로, 1보다 크거나 같은 실수 값을 갖는다.
식 (19)를 이용하여 최대 기존 BL-ASM의 전파 거리 제한 조건식 (8)과 대역폭 제한 조건식 (12)를 다음과 같이 수정할 수 있다.
식 (20)과 (21)에 의해 sampling factor α가 증가하면, 즉 표본화 간격이 증가하면 최대 전파 거리가 감소하여 기존 BL-ASM이 유효하지 않던 거리에서도 대역폭을 제한할 수 있다. 따라서, 동일한 전파 거리에서 고주파수를 제한하는 효과가 생기게 된다.
그림 11은 sampling factor α에 따라 달라지는 최대 전파 거리 조건식 dmax(u;a)과 대역폭 제한 조건식 ubl(d;a)를 나타낸 그래프이다. 이 그래프에서 x축은 전파하고자 하는 신호의 공간 주파수 범위를 나타내고, y축은 전파 거리를 나타낸다. x축과 y축으로 이루어진 좌표계에 그려진 그래프는 표본화 간격은 6.4㎛, 표본화 개수는 1,024, 단파장의 길이는 (Green)를 사용하였다. 그림 11의 화살표 (1)은 α를 1에서 2로 키울 경우 aliasing 없이 온전히 전파할 수 있는 전파 거리가 줄어듦을 보여주고 있다. 그림 11의 화살표 (2)는 동일한 전파 거리로 전파하는 경우, α가 1일 경우보다 α가 2일 경우에 aliasing 없이 전파할 수 있는 대역폭의 크기가 줄어듦을 보여주고 있다. 또한 sampling factor α가 커질수록 aliasing 없이 전파할 수 있는 대역폭의 크기가 점진적으로 줄어들고 있음을 보여주고 있으며, 이는 표본화 간격의 크기를 키움으로써 고주파수 성분을 제한하는 효과가 생김을 보여준다.
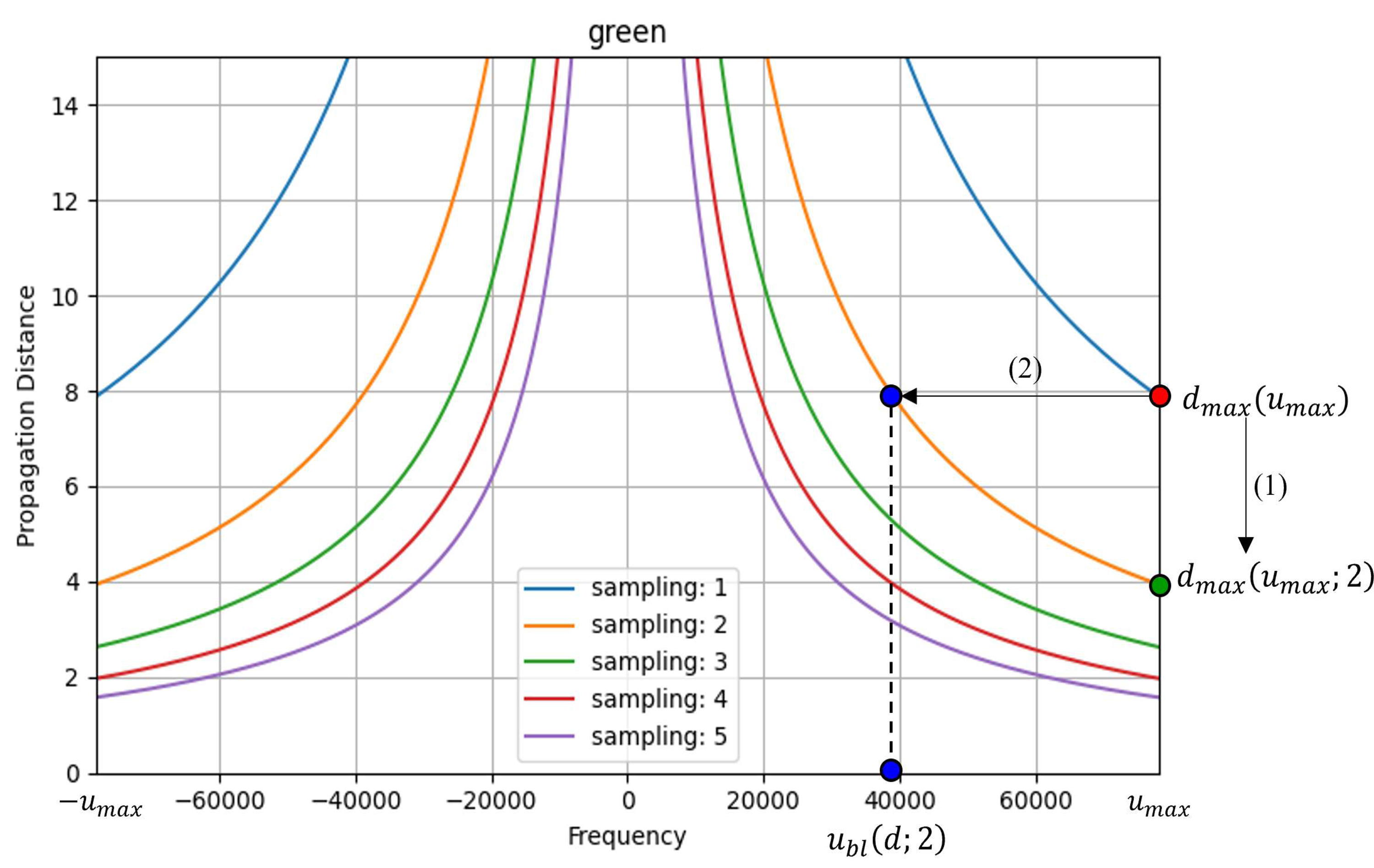
Sampling factor 관점에서 aliasing 없이 전파하는 방법Fig. 11. How to propagate the original signal without aliasing in terms of sampling factor
식 (21)의 대역폭 제한 조건식을 통해 sampling factor α를 추가하므로써 기존 BL-ASM 식 (13) ~(15)를 다음의 식 (22)~(24)와 같이 확장할 수 있다. 본 논문에서는 편의상 식 (22)~(24)로 정의된 새로운 BL-ASM 방법을 BL-ASM(α)라 칭하기로 한다. BL-ASM(α)에서 α가 1일 경우에는 기존 BL-ASM 방법과 동일하게 사용되며, α를 증가시키면 동일한 전파거리로 전파할 때 고주파수 영역을 추가로 더 제거할 수 있다.
그림 12는 BL-ASM(α)를 활용하여 DPAC를 통해 얻은 위상 홀로그램을 복원해 본 결과를 나타낸다. 이때 사용한 실험 조건은 3절의 2번째 실험과 동일하며, 다만 sampling factor α를 변화시켜가며 실험해보았다. 그림 12의 가로축은 전파 거리, 세로축은 복원 화질 평과 결과를 나타낸다. 검은색 실선은 3절의 1번째 실험, 즉 복소 홀로그램 복원 결과를 나타내며, α = 1로 표시된 파란색 실선은 3절의 2번째 실험 중 DPAC로 만들어진 위상 홀로그램 복원 결과를 나타낸다. α를 바꾸어가며 실험한 결과, 기존 복원성능이 떨어졌던 거리(d<dmax(umax) ≃ 7.877218cm)에 대해서도 복원성능을 충분히 향상시킬 수 있음을 확인하였다.
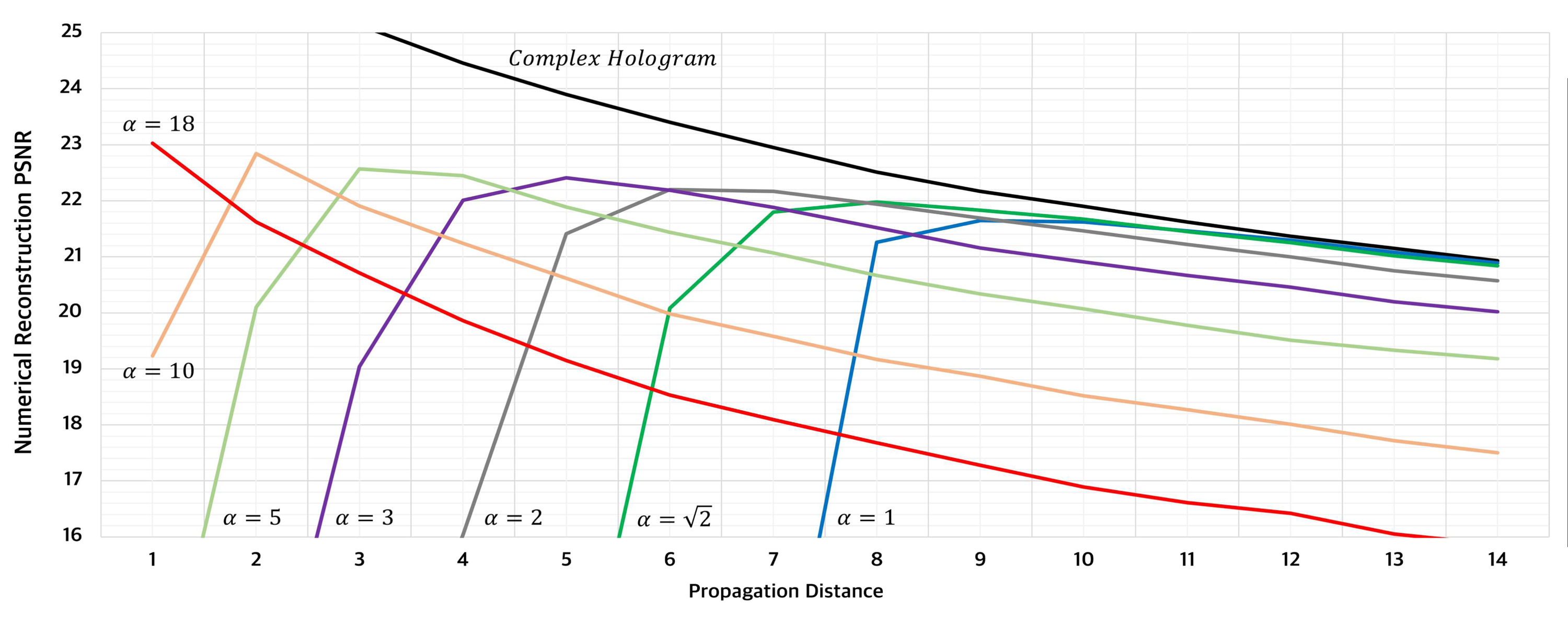
Sampling factor와 전파 거리에 따른 위상 홀로그램 복원 화질 성능 비교Fig. 12. Comparison of PoH Numerical Reconstruction PSNR in terms of sampling factor and propagation distance
다만, 각 sampling factor에 대해 특정 전파 거리를 기준으로 더 멀리 전파하거나 가깝게 전파했을 때 복원성능이 떨어지는 모습을 보이는 경향이 있다. 예를 들어, α = 3인 경우, 5㎝의 전파 거리로 전파했을 때 가장 좋은 복원성능을 보여주었으며, 그보다 더 가깝게 전파하거나 멀리 전파하는 경우 복원성능이 떨어지는 모습을 보여주고 있다. 좋은 복원성능을 내는 거리를 da*라고 했을 때, 전파 거리 d<da*인 경우 DPAC의 subsampling으로 만들어진 aliasing을 충분히 제거하지 않았기 때문이며, 전파 거리 da*<d인 경우 과도한 대역폭 제한으로 위상 홀로그램이 갖고 있던 원본 신호에 대한 정보를 많이 손실했기 때문이다.
그림 13은 각 전파 거리에 대해 가장 좋은 복원성능을 보인 sampling factor를 그래프로 나타낸 것이다. 그림 13의 가로축은 전파 거리, 세로축은 sampling factor를 나타낸다. 각 전파 거리에 따라 복원성능이 가장 좋게 나오는 최적의 sampling factor를 ad*라고 하면, 전파 거리가 작아질수록 ad*가 커져야 복원성능이 향상됨을 알 수 있다. 이는, 전파 거리가 작을수록 대역폭을 더 많이 제한해야 aliasing을 제거할 수 있음을 의미하며, 이를 반영하기 위해 더 큰 sampling factor를 사용해야 함을 의미한다. 반대로 전파 거리가 커질수록 ad*가 1에 가깝게 수렴하는 것을 알 수 있는데, 이는 기존 BL-ASM으로도 충분한 대역폭 제한이 걸려 subsampling에 의한 aliasing을 잘 제어할 수 있기 때문이다.
Ⅴ. 신경망을 통한 위상 홀로그램 생성
일반적으로 신경망을 통해 위상 홀로그램을 생성하는 네트워크를 설계한다면, 해상도를 줄이면서 multi-scale feature map을 추출한 후, transposed convolution 혹은 subpixel convolution[14] 등의 방법을 이용해 다시 해상도를 늘리면서 위상 홀로그램을 생성하게 된다. 하지만 이렇게 해상도를 늘리는 과정에서 앞서 위상 홀로그램을 생성하는데 문제가 생겼던 DPAC 기법처럼 subsampling 하는 효과가 나타나므로, DPAC과 마찬가지로 특정 전파 거리 d이하에서 성능 저하가 발생할 수 있다. 다만, 수식 및 알고리즘을 기반으로 하는 DPAC 기법과는 달리 위상 홀로그램을 생성하는 최적의 파라미터들을 학습하는 과정이기 때문에, subsampling 했을 때 나타나는 문제들을 error backpropagation을 통해 보상해주어 동일한 d에서 DPAC보다는 성능 저하가 적을 가능성이 있다. 본 절에서는 이런 질문에 답하기 위해, 신경망 기반으로 생성한 위상 홀로그램의 복원성능을 d에 따라 실험적으로 분석해보고자 한다.
위상 홀로그램 생성 네트워크로 사용한 신경망은 [11]과 같은 U-net 구조를 사용하였으며, 동일한 학습 전략을 사용하였다. 그림 14는 본논문에서 사용된 신경망 기반 위상 홀로그램 생성 모델의 구조와 학습 방법을 나타낸다. 원본 이미지 X가 들어오면, 첫 번째 신경망 fnet1에 입력으로 넣어 초기 위상 θ을 생성한다. 그 다음, 초기 홀로그램 Xexp(iθ)를 전파 거리 d만큼 전파해 복소 홀로그램, X'exp(iθ')을 생성한 후, 진폭과 위상 정보를 분리해 두 번째 신경망 fnet2의 입력으로 넣어 최종적으로 위상 홀로그램 exp(iϕ)를 생성한다. 생성된 위상 홀로그램을 BL-ASM을 통해 수치적으로 복원한 결과와 원본 이미지와의 차이를 계산해 fnet1,fnet2를 학습한다.
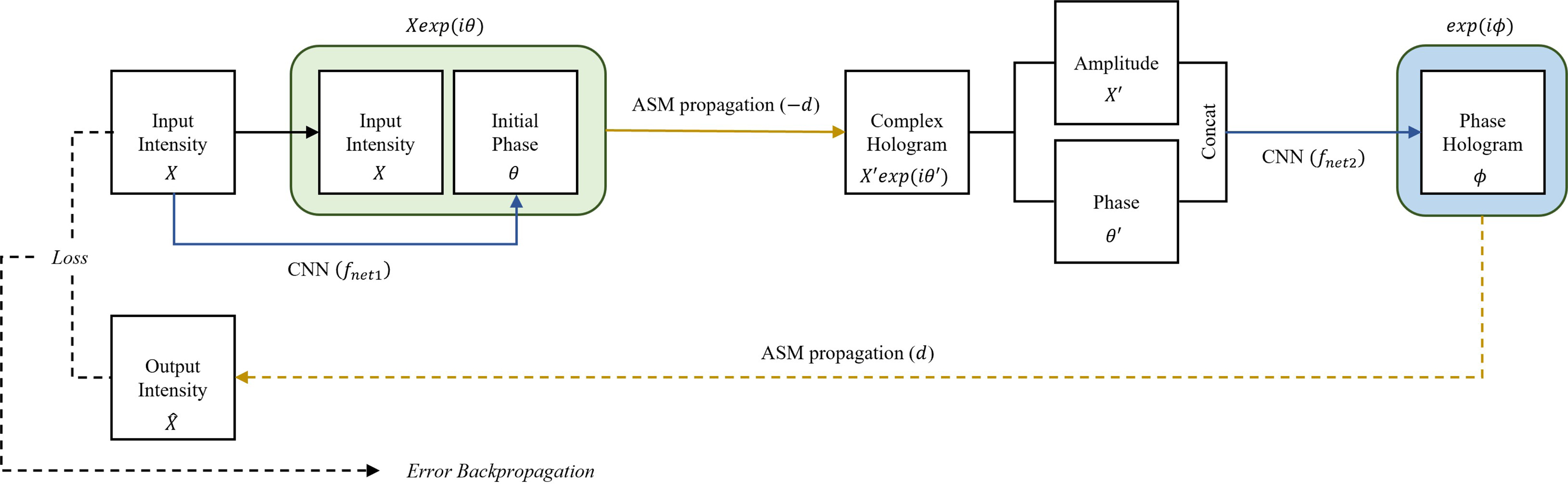
위상 홀로그램 생성 모델 구조 및 학습 방법 개요Fig. 14. Architecture and Training Strategy for Neural Network based Phase-only Hologram Generation
학습에 사용한 데이터는 DIV2K training dataset을 활용했으며, 각 이미지를 512 ×512 크기로 랜덤하게 3장씩 잘라내 총 2,400장의 학습 데이터를 사용하였다. 검증에 사용한 데이터와 표본화 간격, 단파장의 길이는 3장에서 수행했던 실험 조건과 동일하게 설정하였다. 목적함수는 [15]에서 제안한 것처럼 MSE Loss와 MS-SSIM Loss의 가중합으로 사용하였으며, 수식으로 나타내면 다음과 같다.
Learning rate는 0.001로 설정하였으며, 최적화 알고리즘은 Adam을 사용하였다. 전파 거리에 따라 서로 다른 신경망을 35 epoch만큼 학습시킨 뒤, 검증 데이터셋으로 가장 좋은 성능을 기록한 모델로 최종 복원성능을 평가하였다.
표 3의 Unet 행과 그림 15의 노란색 점선은 학습된 신경망 모델을 이용하여 위상 홀로그램 생성한 후 수치복원 domain에서 원본 영상과의 PSNR을 측정한 결과를 나타낸다. 신경망 기반 모델이 DPAC을 사용했을 때보다 모든 전파 거리 d에서 좋은 화질의 위상 홀로그램을 얻을 수 있었지만, 특정 전파 거리에 대해서는 여전히 GS-algorithm보다 못한 성능을 보이고 있었다. 또한, 복원성능 변화 역시 복소 홀로그램처럼 d가 커질수록 떨어지는 것이 아닌, 특정 d에서 성능이 좋아졌다가 거리가 멀어질수록 성능이 떨어지는 모습을 보인다. 특히 DPAC과 마찬가지로 d가 7㎝에서 8㎝로 넘어갈 때, 급격한 성능 향상을 보이고 있는데, 이는 앞서 예상했던 것처럼 신경망에서 위상 홀로그램을 생성할 때 사용하는 layer의 특성에 기반한 것으로 보이며, 최적의 위상 홀로그램을 생성하는 파라미터들을 학습하는 과정에서 DPAC보다 성능은 향상되었지만, 특정 거리 이하의 성능이 여전히 낮음을 알 수 있다.
앞서 DPAC으로 생성한 위상 홀로그램을 복원할 때 subsampling에 의해 발생한 aliasing을 제거하기 위해 본 논문의 확장된 BL-ASM 방법, BL-ASM(α)을 통해 sampling factor를 늘려 고주파수 성분을 제한했던 것처럼, 위상 홀로그램을 생성하는 신경망을 학습할 때도 BL-ASM(α) 방법을 적용하면 성능 개선이 가능한지 확인해보고자 한다. 표 3의 Unet (Limited) 행과 그림 15의 노란색 실선은 본 논문의 확장된 BL-ASM 방법을 통해 학습된 신경망 모델을 이용하여 위상 홀로그램 생성한 후 수치 복원 domain에서 원본 영상과의 PSNR을 측정한 결과를 나타낸다. 표 3의 Unet (Limited)에는 각 전파 거리별로 최적의 성능을 보이는 sampling factor ad*에서의 성능을 표시하였다.

신경망으로 생성한 Phase-only Hologram 복원 화질 평가 결과Table. 3. Numerical Reconstruction PSNR Result of Phase-only Hologram generated with Neural Network
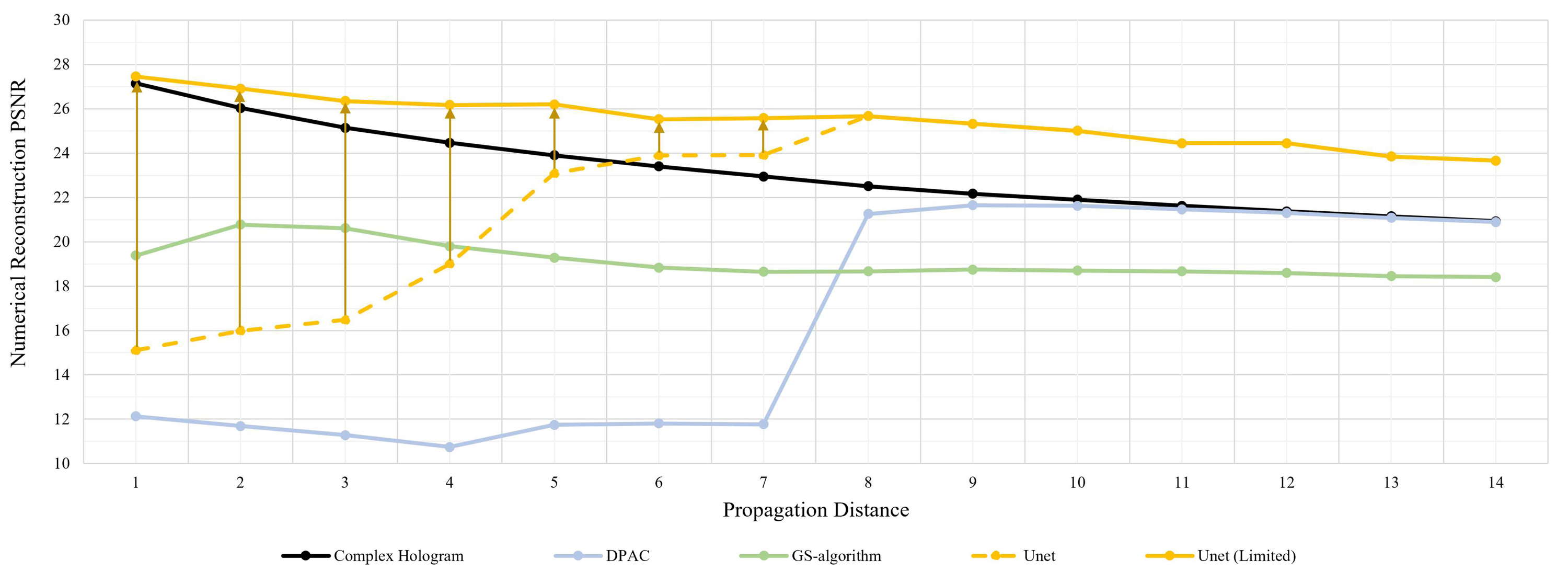
신경망으로 생성한 Phase-only Hologram 복원 화질 평가 결과Fig. 15. Numerical Reconstruction PSNR Result of Phase-only Hologram generated with Neural Network
DPAC에서와 유사하게 1㎝~7㎝ 사이의 전파 거리에서 고주파수 성분을 제한하지 않은 상태로 학습했을 때보다 기존 BL-ASM을 확장한 BL-ASM(α)를 사용해 표본화 간격을 늘려 고주파수 성분을 제한하여 학습했을 때 성능이 향상된 모습을 볼 수 있었다. 또한, DPAC의 경우와 마찬가지로 짧은 전파 거리로 전파할수록 sampling factor의 크기를 키워 대역폭 제한 범위를 키워야 더 좋은 성능을 내기 유리하다는 것을 알 수 있다. 즉, transposed convolution 및 sub-pixel convolution 방법을 이용해 위상 홀로그램을 생성하는 신경망 역시 subsampling에 의해 aliasing을 추가로 발생시킬 수 있으며, 이 aliasing을 제한한 상태로 학습해야 더 좋은 복원성능을 지닌 위상 홀로그램을 생성 및 복원할 수 있음을 알 수 있다.
Ⅵ. 결 론
본 논문에서는 위상 홀로그램을 생성하는 데 있어 전파 거리에 따라 복원성능이 어떻게 달라지는지 확인해보았다. BL-ASM을 사용하면 위상 홀로그램의 경우에도 복소 홀로그램과 마찬가지로 전반적으로 전파 거리가 커질수록 복원성능이 떨어지는 양상을 보였지만, DPAC 및 신경망을 통해 위상 홀로그램을 생성하는 경우, subsampling에 의해 aliasing이 발생하여 특정 거리 이하에서 복원성능이 매우 저하됨을 확인할 수 있었다. 본 논문에서는 이를 해결하기 위한 방법으로 최대 전파 거리 제한 조건을 넘도록 전파하거나, BL-ASM 전달 함수의 공간 주파수가 제한되지 않는, 최대 전파 거리 이하에 대해서도 고주파수 성분을 추가로 제한하여 전파하는 것을 제안하였으며, 두 번째 방법에 의해 위상 홀로그램에서도 복원성능이 향상됨을 알 수 있었다. 마찬가지로 신경망을 사용해 위상 홀로그램을 생성할 때 역시 subsampling에 의해 특정 거리에서 학습이 제한되는 모습을 보였으며, BL-ASM 전달 함수의 공간 주파수 제한을 걸어 학습했을 때, 더욱 안정적으로 좋은 화질의 위상 홀로그램을 생성하는 모습을 보였다.
Notes
References
-
GABOR, Dennis, A new microscopic principle, nature, (1948), 161, p777-778.
[https://doi.org/10.1038/161777a0]

-
ZHANG, Zichen, YOU, Zheng, CHU, Daping, Fundamentals of phase-only liquid crystal on silicon (LCOS) devices, Light: Science & Applications, (2014), 3(10), pe213-e213.
[https://doi.org/10.1038/lsa.2014.94]

-
OSTEN, Wolfgang, et al. , Recent advances in digital holography, Applied optics, (2014), 53(27), pG44-G63.
[https://doi.org/10.1364/photonics.2014.t2c.1]

-
MATSUSHIMA, Kyoji, Formulation of the rotational transformation of wave fields and their application to digital holography, Applied optics, (2008), 47(19), pD110-D116.
[https://doi.org/10.1364/ao.47.00d110]

-
MATSUSHIMA, Kyoji, SHIMOBABA, Tomoyoshi, Band-limited angular spectrum method for numerical simulation of free-space propagation in far and near fields, Optics express, (2009), 17(22), p19662-19673.
[https://doi.org/10.1364/oe.17.019662]

-
MAIMONE, Andrew, GEORGIOU, Andreas, KOLLIN, Joel S, Holographic near-eye displays for virtual and augmented reality, ACM Transactions on Graphics (Tog), (2017), 36(4), p1-16.
[https://doi.org/10.1145/3072959.3073624]

-
HSUEH, Chung-Kai, SAWCHUK, Alexander A, Computer-generated double-phase holograms, Applied optics, (1978), 17(24), p3874-3883.
[https://doi.org/10.1364/ao.17.003874]

- GERCHBERG, Ralph W, A practical algorithm for the determination of plane from image and diffraction pictures, Optik, (1972), 35(2), p237-246.
-
HORISAKI, Ryoichi, TAKAGI, Ryosuke, TANIDA, Jun, Deep-learning-generated holography, Applied optics, (2018), 57(14), p3859-3863.
[https://doi.org/10.1364/ao.57.003859]

-
EYBPOSH, M. Hossein, et al. , DeepCGH: 3D computer-generated holography using deep learning, Optics Express, (2020), 28(18), p26636-26650.
[https://doi.org/10.1364/oe.399624]

-
PENG, Yifan, et al. , Neural holography with camera-in-the-loop training, ACM Transactions on Graphics (TOG), (2020), 39(6), p1-14.
[https://doi.org/10.1145/3414685.3417802]

-
SHI, Liang, et al. , Towards real-time photorealistic 3D holography with deep neural networks, Nature, (2021), 591(7849), p234-239.
[https://doi.org/10.1038/s41586-020-03152-0]

-
AGUSTSSON, Eirikur, TIMOFTE, Radu, Ntire 2017 challenge on single image super-resolution: Dataset and study, Proceedings of the IEEE conference on computer vision and pattern recognition workshops, (2017), p126-135.
[https://doi.org/10.1109/cvprw.2017.150]

-
SHI, Wenzhe, et al. , Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network, Proceedings of the IEEE conference on computer vision and pattern recognition, (2016), p1874-1883.
[https://doi.org/10.1109/cvpr.2016.207]

-
YU, Ting, et al. , Phase dual-resolution networks for a computer-generated hologram, Optics Express, (2022), 30(2), p2378-2389.
[https://doi.org/10.1364/oe.448996]

차 준 영
- 2017년 3월 ~ 현재 : 경희대학교 소프트웨어융합학과 학사
- 주관심분야 : 영상 처리, 비디오 부호화, 딥러닝, 디지털 홀로그램
반 현 민
- 2021년 8월 : 경희대학교 컴퓨터공학과 학사
- 2021년 8월 ~ 현재 : 경희대학교 컴퓨터공학과 석사
- 주관심분야: 영상 처리, 비디오 부호화, 딥러닝, 디지털 홀로그램
최 승 미
- 2022년 : 경희대학교 컴퓨터공학과 학사
- 2022년 ~ 현재 : 경희대학교 컴퓨터공학과 석사과정
- 주관심분야 : 영상 처리, 인공지능, 디지털 홀로그램
김 진 웅
- 1983년 ~ 현재 : 한국전자통신연구원 재직중 (연구전문위원)
- 그 외 : ETRI 방송미디어연구소장 역임, 실감미디어포럼 운영위원장, 한국방송․미디어공학회 종신회원/평의원
- 주관심분야 : 디지털 방송, 멀티미디어 신호 처리, 3D 입체 영상 및 디지털 홀로그래피
김 휘 용
- 1994년 8월 : KAIST 전기및전자공학과 공학사
- 1998년 2월 : KAIST 전기및전자공학과 공학석사
- 2004년 2월 : KAIST 전기및전자공학과 공학박사
- 2003년 8월 ~ 2005년 10월 : ㈜애드팍테크놀러지 멀티미디어팀 팀장
- 2005년 11월 ~ 2019년 8월 : 한국전자통신연구원(ETRI) 실감AV연구그룹 그룹장
- 2013년 9월 ~ 2014년 8월 : Univ. of Southern California (USC) Visiting Scholar
- 2019년 9월 ~ 2020년 2월 : 숙명여자대학교 전자공학전공 부교수
- 2020년 3월 ~ 현재 : 경희대학교 컴퓨터공학과 부교수
- 주관심분야 : 비디오 부호화, 딥러닝 영상처리, 디지털 홀로그램