심층 합성곱 신경망을 이용한 레이더 신호 탐지 성능 분석
Copyright © 2023 Korean Institute of Broadcast and Media Engineers. All rights reserved.
“This is an Open-Access article distributed under the terms of the Creative Commons BY-NC-ND (http://creativecommons.org/licenses/by-nc-nd/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited and not altered.”
초록
최근 인공신경망을 레이더 탐지에 활용하기 위한 연구가 활발히 진행되고 있다. 이에 따라, 본 논문에서는 SOTA(State Of The Art) 신경망을 레이더 탐지에 적용한 성능을 비교한다. 제안하는 신호 탐지 네트워크는 표적의 위치와 도플러 주파수를 감지하는 두 개의 경로로 구성된다. 사용된 네트워크 중 HRNet은 위치 탐지에서 가장 좋은 성능을 보였으며, EfficientNet은 도플러 주파수 예측에 가장 좋은 성능을 보였다. 본 논문의 실험 결과에 따르면, 인공신경망을 적용할 경우, 기존 레이더 신호 처리 결과보다 탐지 확률이 다소 낮지만, 탐지 임계값에 둔감하고 오경보율이 임곗값에 무관하게 매우 낮음을 확인하였다. 위와 같은 실험 결과에 따라 SOTA 네트워크는 레이더 탐지에 잘 활용될 수 있을 것으로 기대된다.
Abstract
Recently, studies to utilize artificial neural networks in radar detection have been actively conducted. In this paper, we compare the performances of SOTA (State Of The Art) neural networks when applying to radar detection. The detection networks consist of two paths to detect the range and Doppler frequency. Among the networks used, HRNet shows the best performance for the range detection, and EfficientNet shows the best performance for Doppler frequency prediction. Although the detection probability is slightly lower than the conventional radar signal processing result, it is somewhat insensitive to the detection threshold, and the false alarm rate is quite low. Therefore, it is expected that the SOTA networks can be well utilized in radar detection.
Keywords:
Binary code, artificial neural network, convolutional neural network, deep learningⅠ. 서 론
인공신경망(Artificial neural network)을 이용한 딥러닝 기반의 물체 탐지 및 식별은 최근 많은 주목을 받는 연구 분야이다. 특히, 합성곱 신경망(CNN, Convolutional Neural Network)은 합성곱(Convolution) 연산을 기반으로 한 신경망으로 데이터의 공간적 연관성을 고려하여 영상과 같은 다차원 데이터 분석에 효율적이다. 예를 들어, 화소(Pixel)별 범주(Category)를 분류하는 영상 분할(Semantic segmentation)은 2015년에 정확도 95.5%에 도달하였으며, 영상 분류(Classification) 정확도는 97%로 이미 인간의 식별 수준을 넘어서고 있다. 잘 알려진 영상 처리 신경망으로는 VGG(Visual Geometry Group at University of Oxford) Nets[1], Res(Residual Networks) Nets[2][3]이나 EfficientNets[4][5] 등이 있으며, 여러 층이 합성곱 층(Convolutional layer)으로 구성되어 영상의 다양한 특징을 추출하는 능력을 가지고 있다[6][7].
이와 같은 신경망들은 이미 대량의 데이터로 학습되어 높은 성능을 보장하고 있으며, 컴퓨터 비전 분야에서뿐만 아니라 다양한 분야에서도 활용되고 있다. 컴퓨터 비전 분야에서 높은 성능을 보이는 신경망을 새로운 분야에 그대로 적용하고 마지막 층만 변경·재학습하는 전이 학습(Transfer learning)은 기학습된 특성을 이용하는 대표적인 예이다[8]. 그러나 레이다 반사 신호의 경우 광학 영상과는 특성이 달라 영상에 의해 학습된 신경망을 전이 학습의 형태로 사용하는 것에는 어려움이 있다. 최근에는 레이다의 탐지에도 위와 같은 딥러닝 기반의 객체 탐지, 영상 분류, 영상 분할 등을 적용하기 위해 많은 연구가 이루어지고 있다[9][10][11]. [9]에서는 채널 어텐션(Channel attention) 기법을 이용하여 합성 개구 레이더(Synthetic Aperture Radar)가 탐지한 표적의 종류를 구별하는 연구를 진행하였다. 이와 유사하게, [10]에서는 합성 개구 레이더 신호를 사용하여 선박의 종류를 구별하는 연구를 진행하였다. 도플러 레이더 신호에 딥러닝을 적용한 연구도 진행되어 [10]에서는 사람 걸음 탐지 및 배경 잡음을 종류를 분류하기 위해 심층 신경망을 사용하였다. 이와 같이, 현재까지 레이더 신호에 딥러닝을 적용한 대부분의 연구는 탐지한 표적의 종류를 구별하거나 배경 잡음의 종류를 구별하기 위한 일반적인 분류 문제로 국한되어 있으며, 영상 형태를 보이지 않는 신호에 대한 연구는 매우 제한적이다.
그러나, 본 논문에서는 이전 연구들과 달리 영상 형태를 보이지 않는 펄스 도플러 레이더의 신호 탐지에 딥러닝을 이용하고자 하며, 원소 단위의 분할 문제로 치환하여 합성곱 신경망의 사용 효과를 최대화하고자 한다. 따라서, 본 논문에서는 레이더 신호 탐지를 위해 대표적인 고성능 영상 처리 합성곱 신경망들의 구조를 적용하나, 전이 학습이 아닌 레이다 데이터로 학습한 후 성능을 비교하고자 하였으며, 일반적인 레이다의 처리 성능과도 비교하였다. 성능 평가에 사용된 데이터는 바이너리 코드로 변조된 펄스 도플러 형태의 파형에 대하여 모의한 반사 신호를 사용하였다.
본 논문은 다음과 같이 구성한다. 2장에서는 레이더의 반사 신호를 모의하는 방법과 생성된 모의 데이터의 구조를 제시하였으며, 3장에서는 탐지에 사용한 신경망의 구조를 설명하였다. 4장에서는 학습된 신경망을 테스트한 결과를 제시하였으며, 5장은 결론을 기술하였다.
Ⅱ. 모의 데이터 생성
1. 레이다 반사 신호
본 논문에서는 펄스 내에 바이너리 코드로 변조된 펄스 도플러 레이다 신호를 가정하고 반사 신호를 모의하였다. 하나의 펄스 반복 주기(PRI, pulse repetition interval) 내의 샘플 수를 M, 바이너리 코드의 길이, 즉 펄스 폭(Pulse width) 내의 샘플 수를 NP 라고 하면 기저 대역에서의 송신 신호 s[k]는 다음과 같이 표현할 수 있다.
| (1) |
따라서 수신된 신호 r[k]는 한 개의 표적 반사 신호와 열잡음 n[k]및 클러터 신호 c[k]의 합으로 다음과 같이 표현할 수 있다.
| (2) |
여기서 A는 표적 반사 신호의 크기, τk는 표적의 거리에 의한 지연 시간, fc는 표적의 이동에 따른 도플러 천이 주파수, i는 연속된 펄스의 순번으로 전체 버스트(BURST)를 N개의 펄스로 구성할 때 i = 1, 2, ⋯, N 의 값을 가진다. 열잡음 신호 n[k]는 표준 가우시안 분포(Normal Gausssian distribution) N(0, 1)로 생성하였으며, 클러터 신호는 다음과 같이 고정된 4개의 점표적으로 모의하였다.
여기서 Al는 클러터 반사 신호의 크기이며, τl는 클러터 거리에 의한 지연 시간이다.
2. 모의 데이터 생성 및 데이터 증강
합성곱 층을 가진 신경망의 학습 데이터 및 실험 데이터로는 앞 절의 식 (2)를 사용하여 회색조(Grayscale) 영상 데이터와 유사한 형태의 2차원 데이터를 생성하였다. 2차원 데이터는 N × M 크기로 펄스별 반사 신호를 N 개의 행으로 정렬하여 전체를 버스트 단위로 생성하며, 이는 일반적인 레이다에서 거리-도플러 맵(Range-Doppler map)의 신호처리 전 상태로 로우 데이터(Raw data)라고 불린다. 또한, 식 (2)에 의해 모의된 신호는 복소 신호이기 때문에 실수 성분(I)과 허수 성분(Q)을 모두 포함하기 위하여 두 개의 입력 채널을 구성하였다.
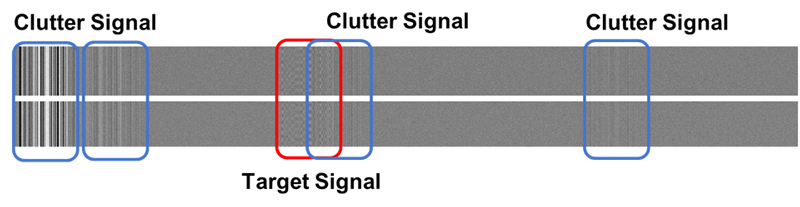
그림 1은 생성한 데이터의 예시를 보여주며 위 행렬과 아래 행렬은 두 개의 입력 채널(I/Q) 데이터이다.
파란 선으로 표시한 영역은 고정된 클러터 반사 신호의 위치이며, 붉은 선으로 표시한 영역은 표적의 반사 신호 위치로 위치(τk), 속도(fc) 및 크기(A)를 랜덤하게 변화시켜 학습을 위한 데이터 세트를 생성하였다. 반사 신호의 도플러 주파수 fd는 펄스 반복 주파수 fprf 내에서 아래 식 (3)과 같이 변경하였으며, 신호 대 잡음비는 수신기의 범위를 고려하여 식 (4)와 같이 변경하였다.
| (3) |
| (4) |
생성한 데이터 세트는 인공신경망 모델이 생성한 모의 반사 신호에만 과적합(Overfitting)되는 것을 방지하고 모델의 일반화 성능을 향상하기 위하여 잡음으로만 구성된 학습 데이터 포함하고, 데이터 증강(Data augmentation)을 통해 다양한 종류의 학습 데이터를 추가로 생성하였다. 데이터 증강 방안으로는 타 레이더의 간섭 신호를 포함하고 다수의 표적 반사 신호도 포함하였다.
본 논문의 실험을 위해서는 위와 같이 생성한 10만 개의 데이터를 레이더 신호 탐지 모델 학습에 사용하였으며, 학습 중 모델은 1,000개의 데이터를 사용하여 검증(Validation)하였다.
Ⅲ. 신호 탐지 네트워크
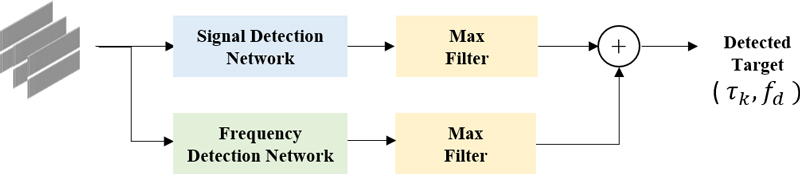
본 논문에서 사용한 레이더 신호 탐지 네트워크는 그림 2와 같이 표적 위치 탐지를 위한 네트워크와 도플러 주파수 탐지를 위한 두 개의 네트워크로 구성하였다.
1. 위치 탐지 네트워크
앞장에서 기술한 2차원 배열 형태로 구성된 데이터의 각 셀은 영상 데이터에서의 행·열 방향의 공간 위치마다 서로 다른 밝기(Intensity)를 가지는 화소와 같이 해석할 수 있다. 이에 따라, 본 논문에서는 표적 반사 신호의 존재 여부는 화소 단위로 속하는 범주를 연관하여 서로 다른 범주를 구성하는 의미론적 영상 분할(Semantic segmentation) 문제로 정의하고, 셀 단위의 신호 존재 여부 판단을 위하여 영상 분할 문제에 효율적인 U-Net[12]과 HRNet(High-resolution network)[13]을 활용하였다. 또한, 표적 신호의 존재 여부가 포함된 네트워크 출력에서 정확한 표적 위치를 탐지하기 위해서는 신호가 존재할 최대 확률이 존재하는 셀을 결정하는 최댓값 필터(Max filter)를 적용하였다. 또한, 일반적으로 펄스 도플러 레이더는 먼저, 펄스 내의 변조 코드에 대하여 정합 필터로 펄스 압축을 수행하고, 이후에 펄스 간 도플러 처리를 통해 신호 대 잡음비(SNR, Signal to Noise)를 개선한 후, 임계치를 넘는 신호에 대해 탐지를 수행하므로 입력단 뒤에 가중치가 고정된 합성곱 층을 추가하여 변조 코드와 합성곱을 수행하였다.
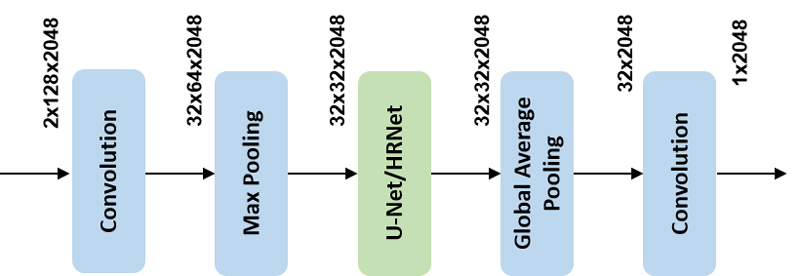
그림 3은 본 논문에서 사용한 U-Net과 HRNet을 활용한 표적 위치 탐지 네트워크의 구조이다.
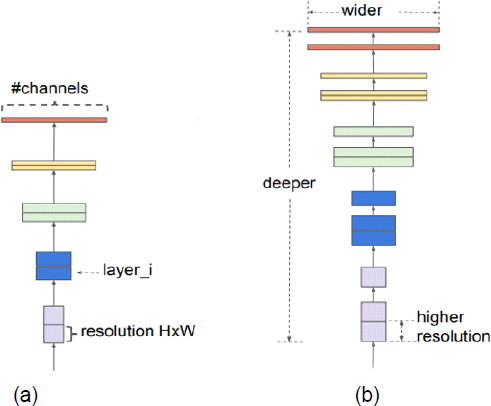
U-Net는 그림 4(a)와 같이 U자 형태의 구조를 가진 네트워크로 일반적인 합성곱 신경망 구조와 같이 풀링(Pooling)을 사용하여 특징 맵(Feature map)의 크기를 순차적으로 줄이고, 원래 입력 크기의 출력으로 복원하기 위하여 디콘볼루션(Deconvolution)을 적용한다. 그러나 특징맵의 크기 축소 과정에서 손실된 정보는 업샘플링(Up-sampling)을 통해서 복원이 어려우므로 U-Net에서는 스킵 연결(Skip connection)을 통해 합성곱(Convolution) 층의 특징 맵을 디콘볼루션 층에 연결하여 특징 맵을 결합(Concatenation)하는 방식으로 정보 손실을 방지한다.
HRNet은 일반적인 합성곱 신경망 구조의 층이 깊어질수록 특징맵의 크기가 줄어들어 정보가 손실되는 한계점을 극복하기 위하여 입력 크기의 특징맵을 출력단까지 유지하면서 층이 깊어질수록 다양한 해상도의 특징맵을 병렬적으로 추가하는 그림 4(b)와 같은 구조이다.
본 논문에서는 위에서 설명한 네트워크들을 레이더 신호 탐지 문제에 적용하기 위하여 신호의 존재 여부를 판단하는 이진 분류 문제에 적합하도록 네트워크 앞 단과 뒤 단에 합성곱 층을 추가하였다. 변형한 네트워크 학습을 위해서는 아래와 같은 이진 교차 엔트로피(Binary cross entropy)를 손실 함수(Loss function) Ld로 사용하였다.
2. 주파수 탐지 네트워크
수신한 신호의 도플러 주파수 탐지 문제는 3.1절의범주 분류 문제와 달리 실수값을 예측하는 회귀(Regression) 문제로 정의하였다. 이에 따라 본 논문에서는 식 (4)의 fd 값을 영상 분류 및 인식 문제에서 현재 높은 성능(SOTA, State-of-the-Art)을 보이는 ResNet과 EfficientNet을 사용하여 회귀 문제에 적용하여 예측하였다.
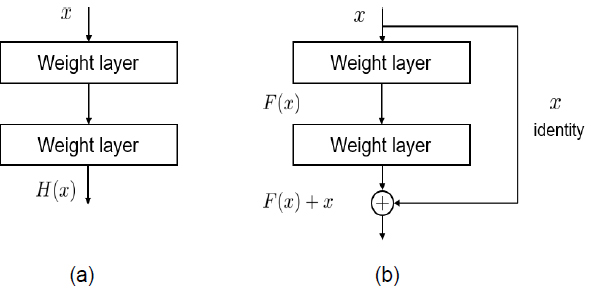
ResNet은 층이 깊은 합성곱 신경망의 성능 정체(Saturation) 및 감쇄(Degradation) 문제를 해결하기 위하여 그림 5(b)와 같이 스킵 연결 구조를 사용하여 층을 연결한다. 그림 5는 일반적인 신경망의 순차적인 층 연결 방식과 ResNet에서 사용하는 층 연결 방식을 비교하여 보여준다. 스킵 연결은 학습 도중 발생한 잔여 에러(Residual)를 보상하는 방법으로 다양한 문제에 대한 높은 성능을 보장한다[3][14].
EfficientNet[7]은 그림 6에서 보는 바와 같이 합성곱 신경망의 성능 향상을 위해 네트워크 모델의 크기를 조절하는 효율적인 방법을 제시한다. 모델의 크기를 조절하는 방법으로는 채널의 개수를 조절하는 방법, 층수를 조절하는 방법, 입력의 해상도를 조절하는 방법이 있으며, EfficientNet은 세 가지의 방법을 모두 고려하여 자원을 효율적으로 사용하면서도 성능을 보장하는 구조이다.
본 논문에서 ResNet과 EfficientNet의 구조를 회귀 문제에 적용하기 위하여 마지막 층인 완전 연결 층(Fully connected layer)을 주파수 탐지에 적합한 구조로 변경한 후, 2.2절에서 구성한 학습 데이터를 활용하여 두 네트워크를 다시 학습하였다. 학습 시 사용한 손실 함수는 배치 내 j번째 학습 데이터의 실제 주파수가 , 예측한 주파수가 일 때, 아래의 평균 제곱 오차(MSE, mean squared error)를 사용하였다.
| (5) |
위의 식에서 tj는 j번째 셀에 실제 신호의 존재 여부(Ground-truth)를 나타내며 신호가 존재할 경우 1, 존재하지 않을 경우 0 값을 가진다. yj는 위치 탐지 네트워크의 출력으로 네트워크가 탐지한 신호가 존재할 확률값이다. Nt는 미니 배치(Mini-batch) 크기가 B일 때 배치에 속하는 모든 학습 데이터들의 셀의 개수로, Nt = 2 × B × N × M 이다.
Ⅳ. 실험 및 고찰
1. 고전 처리방식에 의한 결과
먼저 비교를 위해 다소 일반적인 레이더 탐지 방식에 의한 탐지 성능을 구해 보았다. 일반적으로 펄스 도플러 레이더는 먼저, 펄스 내의 변조 코드에 대하여 정합 필터로 펄스 압축을 수행하고, 이후에 펄스간 도플러 처리를 통해 신호대 잡음비를 개선한 후, 임계치를 넘는 신호에 대해 탐지를 수행한다. 임계치는 오탐지 확률(False alarm rate)에 의해 결정되며, 이에 따라 최종 탐지확률이 결정된다.
제안된 신호망 네트워크의 성능시험에 사용된 데이터에 대하여 일반적인 레이더 신호처리를 수행한 결과는 그림 7과 같다. x축의 신호대 잡음비는 입력 신호에서의 비이며, 코드 길이 128과 펄스 수 128에 의해 처리 손실을 고려하여 신호처리 이득은 약 35dB정도이다.
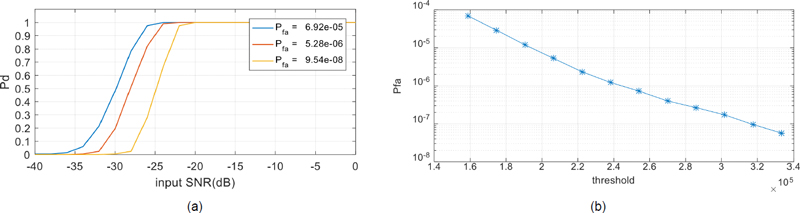
Detection performance (a) false alarm rate and detection probability (b) false alarm rate with different thresholds
이어서 3장에서 설명한 네트워크를 사용하여 레이다 신호에 대한 탐지 성능 평가를 수행한 결과는 다음과 같다. 레이다 신호 위치 및 주파수 예측 시험(Test)을 위해서는 128 × 2048(N × M) 크기의 101,000개의 데이터를 사용하여 성능을 평가하였으며, 신호의 위치 및 도플러 주파수는 각 데이터마다 랜덤하게 설정하였다. 또한, 오탐지 확률 평가를 위해서는 랜덤한 잡음으로 구성된 128 × 2048 크기의 100,000개의 데이터를 사용하였다. 모든 실험은 Intel i7-10700K 프로세서 8코어 CPU와 NVIDIA RTX 3090, 32GB 메모리가 장착된 컴퓨터 환경에서 수행하였다.
2. 위치 탐지 성능
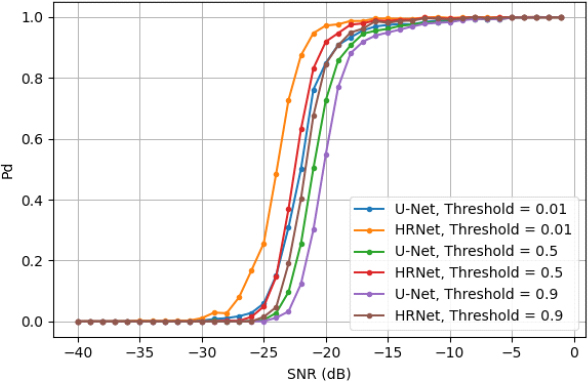
3.1절의 위치 탐지 네트워크 학습에는 최적화 알고리즘으로 AdamW(Adaptive moment estimation with decoupled weight decay)[15]를 사용하였으며, 학습률(Learning rate)은 1 × 10-4를 사용하였다. 학습은 10번의 에폭(epoch) 동안 검증 오차가 감소하지 않으면 종료하도록 설정하였으며, 약 5.7만 이터레이션(Iteration) 동안 학습을 수행하였다. 또한, 실험에 사용한 미니 배치 크기(B)는 35로 설정하였으며, 활성 함수(Activation function)로는 시그모이드(sigmoid) 함수를 사용하였다. 사용한 네트워크들의 위치 탐지 성능 비교를 위하여 설정한 임계치(Threshold)는 활성 함수의 출력에 범위에 따라 0에서 1사의 숫자로 설정하였으며, 서로 다른 임계치에 따른 위치 탐지확률은 그림 8과 같다.
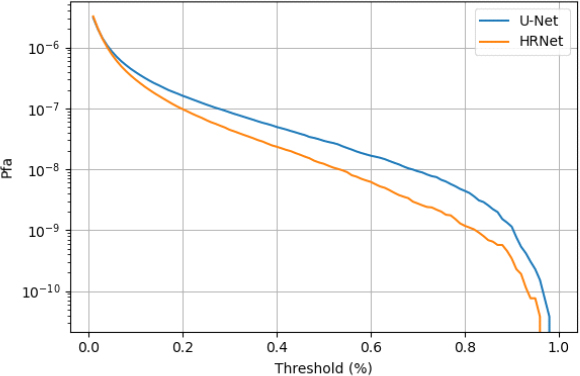
HRNet이 U-Net에 비하여 동일한 신호대잡음비에서 높은 탐지 확률을 보이는데, 이는 HRNet이 고해상도 특징맵을 유지함으로써 정보 손실을 최소화하여 패턴의 미세한 특징을 학습 결과에 반영할 수 있기 때문으로 해석할 수 있다. 또한, HRNet의 경우에는 다양한 해상도의 특징맵을 결합하여 미세한 패턴의 특징뿐만 아니라 저해상도의 특징맵에서는 입력 전체의 패턴도 효율적으로 추출하는 것으로 해석할 수 있다. 여기에서 사용한 임계치는 앞 절의 임계치와 다른 수치이므로 이를 비교하기 위해 오탐률을 분석해 보았다. 그림 9는 사용된 임계치에 따른 오탐지 확률을 측정한 결과로 동일한 신호대잡음비에서 HRNet은 U-Net보다 낮은 오탐지 확률로 성능 우위를 보임을 알 수 있다.
앞 절에서 제시한 고전적인 레이더의 탐지 성능에 비해 –20dB이하의 낮은 신호대 잡음비에서 탐지 확률은 낮게 측정되지만, 임계치의 변화에 따른 탐지 확률의 변화가 작고, 오탐률도 매우 낮은 특징을 가진다.
3. 주파수 탐지 성능
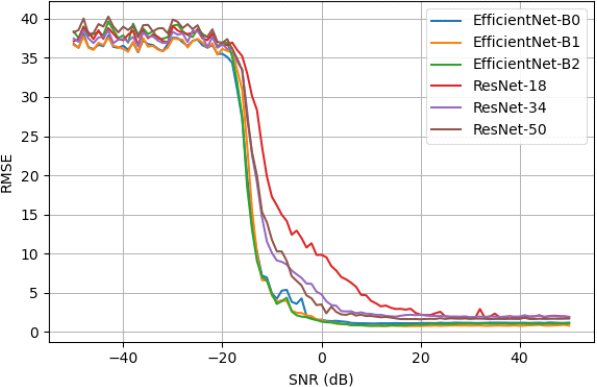
주파수 탐지 성능 분석을 위해서는 6개의 모델 ResNet-18, ResNet-34, ResNet-50, EfficientNet-B0, EfficientNet-B1, EfficientNet-B2을 사용하여 평가하였다. 네트워크의 학습을 위해서는 최적화 알고리즘으로 AdamW[16]를 사용하였으며, 학습률은 1 × 10-4를 사용하였으며, 학습은 10번의 에폭동안 검증 오차가 감소하지 않으면 종료하도록 설정하였다. 각 네트워크 별로 약 5.1만, 6.0만, 8.6만, 7.7만, 9.4만, 10.5만, 12.7만 이터레이션 동안 학습을 수행하였다. 실험에 사용한 미니 배치 크기는 35로 설정하였다.
그림 10의 결과와 같이 모델의 다양성에도 불구하고 EfficientNet이 ResNet에 비하여 높은 주파수 추정 정확도를 보이며, 설정한 주파수 범위(1-128) 내에서 신호대잡음비가 0일 때 약 10% 정도의 오차를 보이는 것으로 분석된다. 이는 ResNet보다 상대적으로 단순한 구조를 가진 EfficientNet이 주어진 레이다 주파수 예측 문제에 적합한 복잡도를 가져 학습에 적합한 구조를 가지는 것으로 해석할 수 있다.
Ⅴ. 결 론
본 논문에서는 현재 높은 성능(SOTA)을 보이는 합성곱 신경망을 활용하여 레이더 신호의 표적 탐지 문제에 적합하도록 변경하여 실험을 수행하고 결과를 분석하였다. 비교에 사용된 합성곱 신경망 중에는 위치 탐지에는 HRNet이 주파수 예측에는 EfficientNet이 좋은 성능을 보이는 것으로 나타났다.
클러터가 없는 환경에서 바이너리 코딩된 펄스 도플러 레이더에 대하여 적용하였을 때, 일반적인 레이더 신호처리 결과에 비해 탐지 확률은 조금 못 미치지만, 임계치에 의한 탐지 확률의 변화가 작고 오탐률도 낮은 것으로 분석되었다. 따라서, SOTA 영상 처리 네트워크를 잘 활용하면, 레이더 분야에서도 좋은 성능을 보일 것으로 예상한다.
Acknowledgments
이 논문은 2022년도 정부(교육부)의 재원으로 한국연구재단 개인연구사업의 지원을 받아 수행된 연구임. (No. 2022R1F1A1062950)
References
- K. Simonyan and A. Zisserman. "Very deep convolutional networks for large-scale image recognition," arXiv preprint 1409.1556, , 2014.
-
K. He, X. Zhang, S. Ren, and J. Sun. "Deep residual learning for image recognition," In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 770-778. 2016.
[https://doi.org/10.1109/CVPR.2016.90]

-
A. Kolesnikov, L. Beyer, X. Zhai, J. Puigcerver, J. Yung, S. Gelly, and N. Houlsby. "Big transfer (BiT): General visual representation learning," European Conference on Computer Vision (ECCV), pp. 491-507, 2020.
[https://doi.org/10.1007/978-3-030-58558-7_29]

- M. Tan, and Q. Le, "EfficientNet: Rethinking model scaling for convolutional neural networks," In International Conference on Machine Learning (ICML), pp. 6105-6114, 2019.
-
Q. Xie, M.-T Luong, E. Hovy, and Q. V. Le, "Self-training with noisy student improves imagenet classification," In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 10687-10698, 2020.
[https://doi.org/ 10.1109/CVPR42600.2020.01070]

-
C. Szegedy, S. Ioffe, V. Vanhoucke, and A. A. Alemi, “Inception-v4, inception-resnet and the impact of residual connections on learning”, In Thirty-first AAAI conference on artificial intelligence, pp. 4278-4284, Feb. 2017.
[https://doi.org/10.1609/aaai.v31i1.11231]

-
M. Z. Hossain, F. Sohel, M. F. Shiratuddin, and H. Laga, “A comprehensive survey of deep learning for image captioning”, ACM Computing Surveys (CsUR), vol. 51, no. 6, pp. 1-36, 2019.
[https://doi.org/10.1145/3295748]

-
S. J. PAN, YANG, Qiang, “A survey on transfer learning”, IEEE Transactions on Knowledge and Data Engineering, vol. 22, no. 10, pp. 1345-1359, 2009.
[https://doi.org/10.1109/TKDE.2009.191]

- J. H. Park, S. M. Seo, and J. H. Yoo, “Channel attention module in convolutional neural network and its application to SAR target recognition under limited angular diversity condition”, Journal of the Korea Institute of Military Science and Technology, vol. 24, no. 2, pp.175-186, 2021.
- S. J. Lee, T. B. Chae, and K. T. Kim, “Analysis of ship classification performances using OpenSARShip DB”, Korean Journal of Remote Sensing, vol. 34, no. 5, pp. 801-810, 2018.
- J. Kwon, S. J. Ha, and N. Kwak, “Human walking detection and background noise classification by deep neural networks for Doppler radars”, The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 29. no. 7, pp. 550-559, 2018.
-
O. Ronneberger, P. Fischer, and T. Brox, "U-Net: Convolutional networks for biomedical image segmentation." In International Conference on Medical Image Computing and Computer-assisted Intervention (MICCAI), pp. 234-241. Springer, Cham, 2015.
[https://doi.org/10.1007/978-3-319-24574-4_28]

-
K. Sun, B. Xiao, D. Liu, and J. Wang, “Deep high-resolution representation learning for human pose estimation,” In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 5693-5703, 2019.
[https://doi.org/10.1109/CVPR.2019.00584]

-
C. Bowen, B. Xiao, J. Wang, H. Shi, T. S. Huang, and L. Zhang. “HigherHRNet: Scale-aware representation learning for bottom-up human pose estimation,” In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 5386-5395. 2020.
[https://doi.org/10.1109/CVPR42600.2020.00543]

- I. Loshchilov and F. Hutter. "Decoupled weight decay regularization," International Conference on Learning Representations (ICLR), 2019.

- 2017년 9월 : 미국 University of California, San Diego 전기컴퓨터공학과 공학박사
- 2017년 ~ 2018년 : 미국 University of California, Los Angeles Postdoctoral Fellow
- 2018년 ~ 현재 : 서울과학기술대학교 조교수
- ORCID : https://orcid.org/0000-0002-3439-5042
- 주관심분야 : 컴퓨터 비전, 기계 학습

- 2021년 8월 : 서울과학기술대학교 공학사
- 2021년 9월 : 울산과학기술대학교 석사과정

- 2004년 8월 : KAIST 기계공학과 공학박사
- 2004년 ~ 2006년 : LG전자 선임연구원
- 2006년 ~ 2007년 : Manum Semiconductor Korea, Senior Staff Engineer
- 2007년 ~ 2013년 : LIGNex1(주) 수석연구원
- 2013년 9월 ~ 현재 : 세종대학교 국방시스템공학과 부교수
- ORCID : https://orcid.org/0000-0001-5118-5509
- 주관심분야 : 레이더 시스템 및 신호처리, MIMO 레이다