K-means Clustering 기반 음악 표절 검사 시간의 단축 방법

1. 이중 분할 그래프 매칭을 이용한 접근

이중 분할 그래프 매칭은 두 멜로디를 노드의 집합으로 변환하고, 유사성을 나타내는 가중치로 연결하는 그래프 기반 접근법이다. 각 노드는 멜로디의 구간을 나타내며, 가중치는 음높이, 길이, 리듬 패턴 등을 기반으로 정량화된다. 최대 가중치의 매칭으로 표절 의심 구간을 식별하며, 이를 통해 멜로디의 세밀한 유사성을 분석할 수 있다.

정밀한 유사성 측정은 멜로디의 각 세그먼트와 노트를 비교하여 미묘한 차이를 감지하며, 이중 분할 그래프 매칭 기법과 결합하여 표절 검출의 정확성을 높인다. 여기서 세그먼트란 멜로디를 일정 길이로 나누어 음높이, 길이, 리듬 패턴 등 음악적 특징을 분석하기 위한 단위를 의미한다. 유사성 측정은 먼저 멜로디를 구성하는 기본 요소인 음높이, 지속 시간 및 박자 정보를 포함하는 데이터로 멜로디를 변환하는 것에서 시작하여 이 데이터는 멜로디의 각 노트를 이중분할 그래프의 노드로 표현할 수 있는 형태로 처리한다. 각 노드는 멜로디의 특정 부분을 나타내며, 노드 간의 연결(edge)은 이들 부분 사이의 유사성을 수치화한 가중치로 표현된다.

이 과정에서 가장 중요한 부분은 edge의 가중치 계산 방법이다. 가중치는 두 멜로디 노드 간의 음악적 유사성을 기반으로 하며, 주로 편집 거리(Edit Distance) 또는 기타 유사성 측정 알고리즘을 사용하여 계산된다. 편집 거리는 한 시퀀스를 다른 시퀀스로 변환하는 데 필요한 최소 편집 작업(삽입, 삭제, 대체)의 수를 측정한다^[4][8]. 이 거리 측정은 멜로디의 미묘한 변화까지도 감지할 수 있는 능력을 제공하며, 표절의 가능성이 있는 부분을 정확히 식별할 수 있도록 한다.

표절 정도를 계산하는 과정은 두 멜로디 간의 유사성을 정량화함으로써 표절 여부를 판단한다. 이 과정은 그래프 매칭 기법을 활용하여 멜로디 사이의 최대 유사성을 찾아내는 것을 목표로 한다. 그래프 기반의 접근 방식에서는 먼저 멜로디를 대표하는 노드들을 생성하고, 이 노드들 사이의 유사성을 기반으로 가중치가 부여된 edge(연결선)를 형성한다. 각 edge의 가중치는 두 멜로디의 해당 부분 사이의 음악적 유사성을 수치상으로 나타내고 멜로디의 음높이, 길이, 박자 등의 요소들을 고려하여 계산되며, 이러한 요소들의 조합은 편집 거리와 같은 알고리즘을 사용하여 결정된다.

앞에서 거론한 바와 같이 최대 가중치 매칭 문제를 해결하는 것이 주된 목표이다. 이 문제를 해결하기 위해 Kuhn-Munkres 알고리즘(또는 헝가리안 알고리즘)과 같은 알고리즘을 사용하여, 각 왼쪽 노드(하나의 멜로디를 대표하는 노드)를 오른쪽 노드(다른 멜로디를 대표하는 노드)와 매칭시키고, 이 매칭이 전체 가중치의 합을 최대화하도록 한다. 이 과정에서 최대 가중치 매칭은 두 멜로디 사이에서 가장 높은 유사성을 보이는 부분을 식별하게 되며, 이 부분이 표절 의심 구간으로 간주할 수 있다. 매칭 결과는 각각 매칭된 노드 쌍 사이의 가중치를 합산하여 계산되며, 이 합은 표절의 정도를 나타내는 지표로 사용된다. 표절 정도가 높은 멜로디는 유사성이 높은 매칭이 많이 발견되며, 이는 강력한 표절 증거로 간주할 수 있다. 반대로, 유사성이 낮거나 매칭이 적은 경우는 표절 가능성이 작다고 평가된다. BMM-Det 방식은 이러한 이중 분할 그래프 매칭을 기반으로 하며, 모든 음악 쌍에 대해 편집 거리(Edit Distance)를 계산한다. 이 방식은 높은 정확성을 보장하지만, 모든 음악 쌍에 대해 이중 매칭 그래프를 생성하고 계산해야 하기 때문에 데이터셋이 커질수록 계산량이 기하급수적으로 증가한다. 따라서 대규모 데이터셋을 처리하거나 실시간 응용에 적용하는 데에는 한계가 있다.

2. K-means Clustering

K-means Clustering은 통계적 데이터 분석에서 사용되는 대표적인 머신러닝 알고리즘 중 하나로, 관측된 데이터를 사전에 정의된 K개의 클러스터로 그룹화하는 비지도 학습 방법이다. 이 알고리즘은 각 클러스터의 중심(centroid)을 나타내는 K개의 점을 초기에 임의로 선택하고, 각 데이터 포인트를 가장 가까운 클러스터 중심에 할당하는 방식으로 작동한다. 할당 후, 클러스터의 중심은 해당 클러스터에 속하는 모든 데이터 포인트의 평균 위치로 업데이트된다. 이 과정은 클러스터의 할당이 더 이상 변하지 않거나 특정 수렴 기준을 만족할 때까지 반복된다.

K-means Clustering의 수행 절차는 첫 단계로, 클러스터링을 시작하기 전에 K개의 초기 중심점을 선택한다. 이 중심점들은 클러스터의 중심을 대표하며, 초기에는 데이터세트에서 무작위로 선택되거나 특정 휴리스틱을 사용하여 선정된다. 중심점의 선택은 클러스터링 결과에 중대한 영향을 미치므로, 때로는 다양한 방법으로 초기 중심점을 여러 번 결정해 최적의 결과를 도출하기도 한다. 두 번째 단계에서는 각 데이터 포인트를 가장 가까운 클러스터 중심에 할당한다. 이 과정에서 각 데이터 포인트와 모든 중심점 간의 거리를 계산하고, 가장 짧은 거리의 클러스터에 데이터 포인트를 할당한다. 이렇게 함으로써, 각 클러스터는 가장 유사한 데이터 포인트들로 구성된다. 세 번째 단계에서는 새로 할당된 데이터 포인트들을 바탕으로 각 클러스터의 중심을 재계산한다. 각 클러스터의 새로운 중심은 해당 클러스터에 속한 모든 데이터 포인트의 평균 위치로 업데이트되며, 이는 클러스터의 응집도를 높이고 중심점을 데이터의 중심으로 조정하는 데 도움을 준다. 마지막 단계는 수렴 확인이다. 클러스터의 중심이 더 이상 크게 변하지 않을 때까지 이전의 두 단계(데이터 할당과 중심점 업데이트)를 반복한다. 클러스터 중심의 변화가 일정 임계값 이하로 떨어지면, 알고리즘은 수렴했다고 판단하고 반복을 종료한다. 이 임계값은 미리 설정되거나, 특정 수의 반복 후에 알고리즘이 자동으로 종료될 수도 있다. 이러한 과정을 통해 K-means Clustering은 데이터 내의 자연스러운 그룹을 식별하고, 이를 통해 데이터의 패턴과 구조를 분석하는 데 유용하다^[13-15].

3. DTW (Dynamic Time Warping)

두 개의 음악 시계열 데이터가 서로 얼마나 유사한지 비교하기 위해 DTW를 사용하였다.

DTW는 시계열 데이터에서 패턴의 유사성을 측정하는 데 사용되는 알고리즘으로, 두 시계열의 각 요소를 매핑하여 최소 거리의 합을 갖는 경로를 찾아낸다. 이 과정은 먼저 거리 행렬을 생성하여 시작한다. 거리 행렬은 두 시계열 간의 모든 가능한 요소 쌍에 대한 거리(예: 유클리디언 거리)를 계산함으로써 구성된다. 이 행렬의 각 셀은 한 시계열의 특정 시점과 다른 시계열의 특정 시점 사이의 거리를 나타낸다. 이 거리 행렬을 바탕으로, DTW 알고리즘은 시작 지점(행렬의 좌측 상단)에서 끝 지점(행렬의 우측 하단)까지의 경로 중 총거리가 최소가 되는 경로를 찾는다. 이 경로를 ‘최적 와핑 경로’라고 부르며, 각 단계에서 이동할 수 있는 경로는 제한되므로 최적 와핑 경로를 찾는 과정에서, 각 단계의 결정은 이전 단계의 결과에 의존하며, 동적 프로그래밍 기법을 사용하여 최소 비용 문제로 접근한다.

이렇게 결정된 최적 와핑 경로는 두 시계열 간의 거리나 유사성을 정량화하는 데 사용되며, 이 거리는 경로상 거리의 합으로 계산한다. 최적 와핑 경로가 결정되면, 두 시계열 간의 시간적 변동을 보정 하면서도 얼마나 유사한지를 평가할 수 있다. 이러한 특성 덕분에 DTW는 시간 축에서 늘어나거나 줄어드는 형태를 보인 시계열 데이터의 유사성 측정에 적합하다^[4][10].

4. DBSCAN (Density-Based Spatial Clustering of Applications with Noise)

DBSCAN은 밀도 기반의 공간 클러스터링 알고리즘으로, 노이즈 및 이상치를 자동으로 분리하고 무시하는 능력이 뛰어나다. 그리고 클러스터의 형태에 대한 가정이 없어 다양한 길이와 불균일한 분포를 가진 데이터에도 적합하다. 본 논문에서는 각 특성의 시간 변화까지 포함하며, DBSCAN은 고밀도 지역을 기반으로 유사한 형태를 잘 묶어 복잡한 시계열 구조를 효과적으로 클러스터링한다. 이런 특성을 기반으로 본 논문은 DBSCAN을 적용하였다.

DBSCAN은 두 개의 주요 파라미터인 eps (epsilon)와 min_samples가 중요한 역할을 한다. Eps는 한 포인트에서 이웃으로 간주할 수 있는 최대 거리를 정의하며, Min_samples는 한 데이터 포인트가 핵심 포인트로 간주하기 위해, 필요한 최소 이웃 수를 나타낸다. 알고리즘은 데이터 포인트를 순회하며, eps 반경 내에 min_samples 이상의 이웃이 있으면 해당 포인트를 핵심 포인트로 식별하고, 클러스터 확장을 시작한다. 핵심 포인트가 아닌 이웃 포인트는 경계 포인트로 분류되고, 클러스터에 속하지 않는 포인트는 노이즈로 간주한다^[5-6][11-12].

이 방식으로 DBSCAN은 지역적 밀도를 기반으로 자연스러운 클러스터를 효과적으로 형성하며, 복잡한 데이터 구조에서도 노이즈를 구분하는데 좋은 성능을 발휘한다.

1. 데이터세트와 표절 기준

본 연구에서 사용된 음악 데이터세트는 저작권 문제가 없는 MIDI 파일을 제공하는 공개 데이터베이스에서 수집되었다. 주요 데이터 출처로는 FreeMidi.org 등 저작권이 만료되었거나 저작권 문제가 없는 MIDI 파일을 제공하는 사이트들을 활용하였다.

이러한 MIDI 파일들은 클래식, 팝, 재즈 등 다양한 장르를 포괄하고 있다.

데이터세트는 200곡의 원본 곡과 200곡의 변형 곡으로 이루어져 있다. 변형 곡은 원본 음악 200곡을 바탕으로 멜로디, 리듬, 음정의 다양한 변형을 가하여 생성된 200곡이다. 변형은 실제 표절 사례와 유사한 조건을 반영하여, 유사성 검사의 성능을 현실적으로 평가할 수 있도록 세 가지 주요 방법으로 이루어졌다.

첫째, 음정 변형은 원본 곡의 음높이를 ±1에서 ±3의 MIDI 번호 범위 내에서 임의로 조정하여 이루어졌으며, 전체 변형 곡의 약 50%를 차지하였다. 이는 멜로디의 큰 변화 없이도 음정만을 조정하여 미세한 표절을 감지할 수 있는지 평가하기 위함이다.

둘째, 리듬 변형은 특정 음표의 길이를 변경하거나 쉼표를 추가하여 새로운 리듬 패턴을 생성하는 방식으로, 전체 변형 곡의 25%에 적용되었다.

셋째, 멜로디 변형은 원본 곡의 멜로디에서 일부 음표를 삭제하거나 새로운 음표를 추가하여 곡의 주요 멜로디 라인을 변경하는 방식으로 수행되었다. 이 방법은 나머지 25%의 변형 곡에 적용되었다.

이와 같은 변형 방식은 실제 표절 사례에서 사용되는 음악적 변형을 최대한 반영하여, 제안된 유사성 검사 방법의 현실적 적용 가능성을 높이는 데 중점을 두었다.

2. 음악 파일의 사전 분류

클러스터링 과정을 통하여 유사도가 높은 음악끼리 그룹화되며, 이는 K-means Clustering 혹은 DBSCAN (Density-ased Spatial Clustering of Applications with Noise)을 통한 알고리즘을 통해 수행된다. 음악은 그들의 패턴의 유사도를 기반으로 여러 클러스터로 분류되며, 이 결과 각 클러스터는 유사한 특성을 가진 음악들로 구성된다. 본 논문에서는 음악 파일 간의 유사도 측정을 위하여 클러스터링별 사전 분류 능력에 관하여 비교하고 그 측정 결과에 기초한 실용적인 클러스터링 방법을 선택한다.

3. Elbow 방법을 통한 최적 클러스터 수 결정

K-means Clustering은 클러스터의 수를 사전에 정의해야 하며, 초기 중심점의 선택과 클러스터의 형태에 따라 결과가 달라질 수 있으므로 K-means Clustering의 성공적인 적용은 클러스터의 수 K를 적절히 선택하는 것에 크게 의존한다는 것이다.

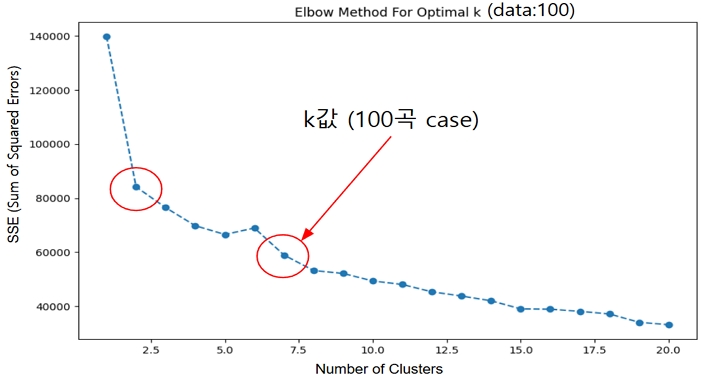
본 논문에서는 Elbow 방법을 사용하여 최적의 K값을 도출하였다. K-means Clustering을 적용하여 다양한 K값에 대해 SSE (Sum of Squared Errors)를 계산하였다. SSE는 클러스터 내 각 점과 해당 클러스터 중심점 사이 거리의 제곱합을 나타낸다. 클러스터 수에 따른 SSE의 변화를 시각화하여, SSE의 감소가 상대적으로 완만해지는 지점을 Elbow로 식별하였다. 코드 구현에서는 1부터 20까지의 K값에 대해 반복적으로 클러스터링을 수행하고 각 경우에 대한 SSE를 기록하였다.

Elbow 지점을 보다 정확히 식별하기 위하여, SSE의 변화율과 그 변화율의 차이(변화율의 변화율)를 계산하였다. 이를 통해 SSE의 감소가 급격히 완만해지는 지점을 프로그래밍적으로 찾아내어 데이터의 클러스터링을 효과적으로 수행할 수 있는 K값을 선정하였다 (그림 1). 이러한 방법을 통해 결정된 Elbow 지점은 클러스터 수를 결정하는 데 중요한 기준으로 사용할 수 있다.

Fig. 1.

Example of K value used in this study (Elbow graph)

4. 유사성 검사의 본 과정

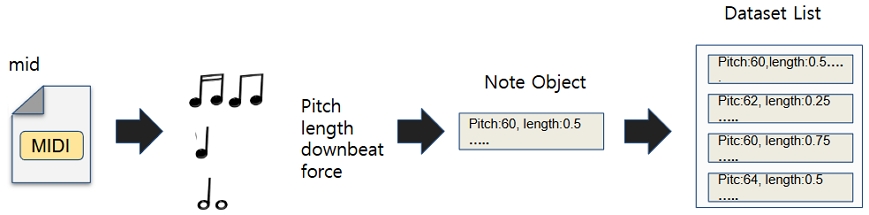
우선 데이터 전처리에서 음악 파일이 MIDI 형식에서 유사도 검사 하기 쉬운 형식으로 변환되어야 한다. 이 단계에서는 MIDI 파일에서 노트 정보를 추출하고, 이를 사용하기 쉬운 형태로 저장하는 역할을 한다. 각 노트의 핵심 특성인 pitch(음높이), length(지속 시간), downbeat(강박 여부), 그리고 force(음의 강도)가 포함되어, 이러한 정보가 다음 단계의 패턴 추출 및 특성 벡터 생성에 활용된다. 그림 2에서 이 과정을 나타낸다.

Fig. 2.

Note list creation process

우선 음악 특징에 따라 음악을 여러 개의 세그먼트로 분할하고, 유사한 특징을 갖는 세그먼트들을 같은 그룹으로 패턴화 한다^[9]. 특성 벡터 생성을 위해 pitch, length의 모든 값을 패턴에 넣고 downbeat와 force는 값이 거의 변하지 않으므로 각각의 평균치를 넣었다. 그리고 각 음악에서 이 패턴들의 발생 빈도를 계산하여 음악의 특성 벡터를 형성한다. 이렇게 추출된 특성 벡터는 K-means Clustering에 사용된다.

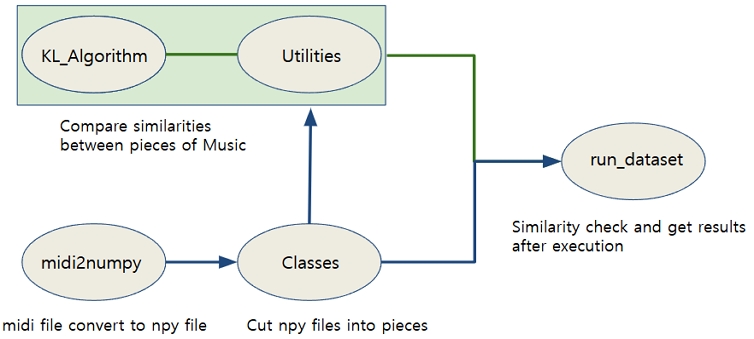
유사도 검사 단계에서 음악 간의 유사도 차이를 계산한다. 특히 두 가지 주요 방법, 즉 편집 거리(Edit Distance)와 최대 흐름(Max Flow) 방법을 사용한다. 편집 거리는 두 음악 조각 간의 유사도를 측정하는 데 사용되며, 최대 흐름 방법은 각 음악 조각 간의 최적의 매칭을 찾아 유사도를 계산한다. 이러한 방법들은 음악의 구조적인 특성과 유사성을 포착하여, 음악 간의 유사도 측정에 사용된다. 그림 3은 기존 BMM-Det의 전체 과정을 나타낸다.

Fig. 3.

Flow chart of similarity measurement process (BMM-Det)

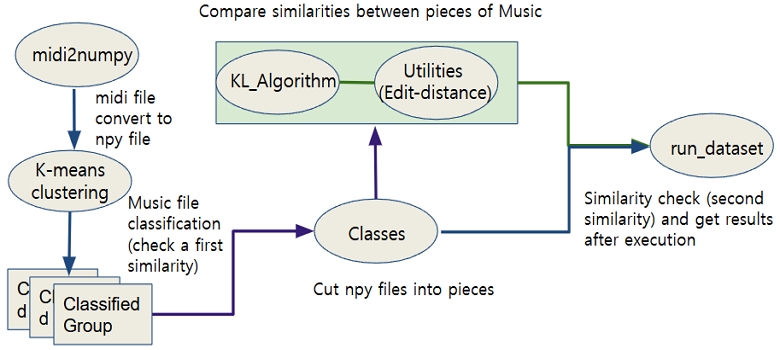
그림 4는 K-means Clustering을 이용한 유사도 측정의 전체 과정을 보여준다.

Fig. 4.

Flow chart of similarity measurement process (K-means clustering)

1. 음악 분류 단계에서의 K-means clustering과 DTW&DBSCAN의 비교

먼저, 사전 분류 단계에서 K-means Clustering과 DTW&DBSCAN 간의 Music Classification Accuracy와 Execute Time을 비교하였다.

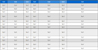
표 1에서 보는 바와 같이 DTW&DBSCAN의 결과가 58개일 때는 352초가 걸렸었는데 80개를 실행하니 1시간 23분 39초로 기하급수적으로 늘어난 것을 볼 수가 있다. 이에 따라 최대 80개의 곡에 대해서만 실험을 진행하였으며, 80개 이상의 곡에 대한 실험은 실험 도중에 멈추어 제외되었다. Music Classification Accuracy는 음악 사전 분류 단계에서 각 클러스터에 유사한 곡이 분류되었는지를 평가하는 것이다. DTW&DBSCAN 방법은 높은 Music Classification Accuracy를 가졌지만, Execute Time이 오래 걸려 유사성 검사에서의 실제 적용이 불가능하므로 DTW&DBSCAN이 아닌 K-means Clustering을 이용하였다.

Table 1.

Comparison between K-means clustering and DTW&DBSCAN

다음, 음악의 유사성 검사에 대하여 기존 논문의 BMM-Det와 본 논문의 Clustering-Det의 성능을 유사성 검사에 의한 Accuracy와 Average Index를 통해 비교하였다. 이는 각 음악 조각이 얼마나 정확하게 그룹화되고, 특정 음악이 해당 클러스터 내에서 어떻게 위치하는지에 대한 평가를 제공한다.

N_c는 정확히 예측된 상위 1개 매칭의 수를 의미하며, 유사성 검사가 정확한 경우를 나타낸다. N_q​는 전체 쿼리의 수를 나타낸다. ∑I_c는 정확히 예측된 매칭의 인덱스 합을 의미하며, 유사성 검사의 평균적 성능을 평가하는 데 사용된다. Accuracy (1)은 가장 유사한 음악 조각이 쿼리 음악 조각과 동일한 원본 음악에서 추출된 것이 얼마나 자주 발생하는지를 나타내며, Average Index (2)는 쿼리 음악 조각과 동일한 원본 음악의 조각이 검색 결과에서 평균적으로 어느 위치에 나타나는지를 알려준다. 다양한 파라미터와 조건변화에 따른 실험을 통해, 어떤 파라미터를 사용할 경우, Average Index와 Accuracy가 높은 값을 가지고 낮은 값을 가지는지에 대한 깊은 이해를 얻을 수 있다.

표 2는 기존 논문의 BMM-Det에서 각각의 매개변수에 따른 Average Index와 Accuracy의 결과를 보여주고, 표 3은 본 논문의 Clustering-Det에서 각각의 매개변수에 따른 Average Index와 Accuracy의 결과를 보여준다. 표 2와 표 3의 매개변수 RelativeDuration은 상대적 지속 시간 시퀀스를 사용하는 것을 의미한다. RelativePitch는 상대적 피치 시퀀스를 사용하는 것을 의미하며, MaxMatch는 시퀀스를 분할하고 최대 가중치 매칭을 계산하는 것을 의미한다. Downbeat는 노트가 다운비트인지 여부를 고려하는 것을 의미한다. NoteDistance는 편집 거리를 계산할 때 피치의 이동을 고려하는 것을 의미한다^[2]. 표 2에서 확인되는 바와 같이 매개변수의 조합에 따라 Average Index와 Accuracy의 차이가 크다. 그에 반하여 표 3은 매개변수의 조합에 따라 Average Index와 Accuracy가 크게 달라지지 않는다. Clustering-Det는 매개변수에 큰 영향을 받지 않아 매개변수의 사용 여부와 변화에도 불구하고 일정 이상의 Accuracy를 나타냄을 의미한다.

Table 2.

Changes according to different parameters (for BMM-Det)

Table 3.

Changes in Accuracy and Average Index according to various parameters (for this study)

한편 유사성 검사의 측정 시간에 관해서 기존 논문의 BMM-Det 논문에서는 음악 파일 간의 유사성을 직접적으로 측정하는 방식이었기 때문에, 전체 데이터세트에 대한 유사성 검사가 필요하므로 계산 복잡도와 실행 시간이 상당히 크게 나타났다. 특히, 큰 데이터세트에서 시간이 수백 배로 늘어났다.

반면에 본 논문의 Clustering-Det 방법에서는 K-means Clustering을 사용하여 전체 음악 파일을 여러 그룹으로 미리 분류하였다. 이렇게 분류된 각 그룹 내에서만 유사성 검사를 수행하므로, 비교 대상이 줄어들게 되어 검사 시간이 단축되었다.

실험은 2개의 데이터세트(58, 200)에 대해 수행되었고, 각 경우에 대해 기존 논문의 BMM-Det 방법과 제안된 Clustering-Det 방법의 Execute Time, Music Classification Accuracy를 측정하였다. 곡 200개에서 실행 시간이 약 64% 줄어든 것을 볼 수 있다 (표 4). 제안된 Clustering-Det 방법은 BMM-Det 방법에 비하여 음악 개수가 증가할수록 유의미하게 검사 시간을 줄일 수 있음을 확인하였다.

Table 4.

Accuracy and measurement time comparison between similarity test methods