삼중항 샘플링 전략과 HNSW 알고리즘을 이용한 딥러닝 기반의 유사 이미지 검색 기법

1. 삼중항 손실

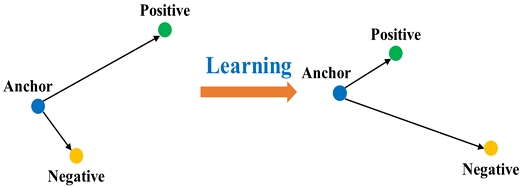
샘플 간의 거리를 이용해 유사도를 학습하기 위해 대조 손실(contrastive loss)과 삼중항 손실을 이용하는 방법이 있다. 대조 손실은 두 샘플 간의 유사성을 고려하여 positive 샘플과의 거리는 최소화하고 negative 샘플과의 거리를 최대화하는 방법으로 학습한다. 그러나 대조 손실은 한 번에 두 개의 샘플만을 고려하므로, 삼중 관계를 이용해 상대적 거리를 학습하는 삼중항 손실보다 학습하기 어렵다. 삼중항 손실은 임베딩 공간에서 anchor 샘플에 대하여 positive 샘플, negative 샘플과의 거리를 동시에 고려해 negative 샘플이 positive 샘플보다 anchor 샘플에 대해 멀어지게 한다. 그림 1은 삼중항 손실을 이용한 학습의 동작 방식이다.

Fig. 1.

Training mechanism based on triplet loss

삼중항 손실은 임베딩 벡터 사이의 상대적 거리 정보를 직접적으로 학습한다. 삼중항은 anchor, positive, negative 세 개의 샘플로 구성된다. 학습은 anchor와 positive 샘플 사이의 거리는 최소화되고 anchor와 negative 샘플 사이의 거리는 최대화되는 방향으로 진행된다. 삼중항 손실 함수는 식 (1)과 같다.

여기서 L(A, P, N)은 삼중항 손실을 나타내며 d(A, P)는 anchor와 positive 샘플 사이의 거리를 의미하고 d(A, N)은 anchor와 negative 샘플 사이의 거리를 의미한다. 또한 α는 positive 샘플과 negative 샘플 사이의 margin을 의미한다. 임의의 α를 설정하여 positive 샘플과 negative 샘플이 일정 거리 이상을 유지하며 멀어지도록 학습한다.

삼중항 손실을 이용해 적절한 임베딩 벡터를 만들어내기 위한 여러 연구가 진행되어왔다. 특히, Hard mining, Easy mining을 통해 positive 중 가장 가까운 샘플 이외의 데이터의 상대적 거리를 멀도록 학습하는 방법이 연구되었다^[4]. 그러나 해당 방법은 positive 샘플에 대한 상대적 거리를 집중적으로 연구하였으며, class 정보를 적극적으로 활용하여 negative 샘플을 구성하지 않은 한계점을 갖고 있다.

2. ANN

임베딩 벡터를 이용하여 유사한 이미지를 찾는 가장 기본적인 형태인 brute force KNN은 모든 후보 벡터와의 유사도를 비교하여 가장 가까운 순서대로 정렬하는 방식이다. 이러한 방식은 검색 대상의 규모에 비례하여 유사도를 비교하는 시간이 늘어나는 단점이 있다. 근사적으로 근접 이웃을 계산하는 ANN의 방법을 이용하여 이러한 문제를 해결할 수 있다.

ANNOY^[5](Approximate Nearest Neighbor Oh Yeah) 방법은 전체 샘플을 이진 트리 형태의 부분들로 나누어 구성하고 트리 탐색 방식으로 특정 샘플이 속하는 구역을 찾은 후 이 구역 안의 샘플 중에서 가장 유사한 샘플을 추출한다.

HNSW^[6](Hierarchical Navigable Small World) 방법은 검색 대상의 수를 계층적으로 늘려가면서 인접 위치를 계산한다. 그림 2와 같이 가장 처음 계층에서 랜덤하게 초기 위치를 설정하고, Greedy Search 알고리즘을 통해 query와 가장 가까운 벡터를 찾아낸다. 해당 벡터의 위치를 더 많은 샘플이 있는 계층에서의 초기 위치로 사용하고 마찬가지로 가장 가까운 벡터를 찾아낸다. 이러한 반복 과정을 통해 전체 샘플과의 비교 없이 인접한 위치와 주변 샘플들을 추출한다.

Fig. 2.

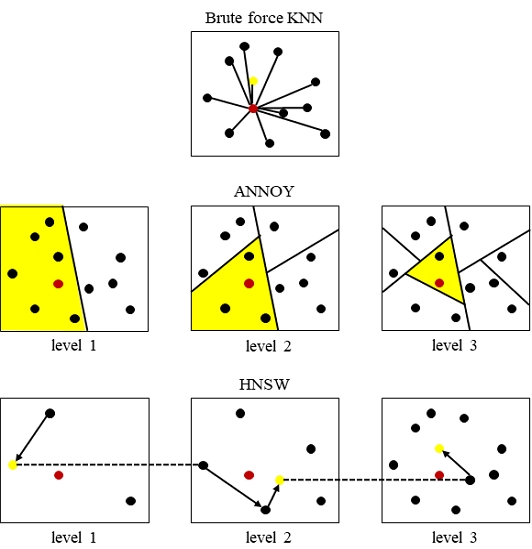
Search method for each algorithm. Processes of finding the node (yellow) closest to the query (red). Brute force KNN compares all nodes, while ANNOY continuously divides sections in each layer in the form of a binary tree and narrows down the section close to the query to find adjacent nodes. HNSW greedily searches for adjacent nodes starting from a random initial node in the first layer and sets them as initial nodes in the next layer with a gradually denser embedding space to find adjacent nodes.

1. 이미지 인코더

유사 이미지 검색 방법은 입력 이미지의 임베딩 벡터와 가장 가까운 벡터에 대응하는 이미지를 찾아내는 것을 목표로 한다. 이를 위해 이미지를 임베딩 벡터로 변환하기 위한 이미지 인코더가 필요하다. 제안하는 방법에서는 Swin Transformer v2-B^[7] 구조를 적용한 이미지 인코더를 사용한다. Swin Transformer v2는 지역적인 self-attention 메커니즘을 도입하여 연산 효율성과 개선된 성능을 갖는 모델로 기존의 CNN 모델 대비 더 풍부한 특징 표현을 제공할 수 있다. 효율적인 학습을 위해 ImageNet 데이터로 사전 학습된 모델로부터 학습을 진행하고 임베딩 벡터의 크기는 2048을 사용한다.

2. 삼중항 샘플링 전략

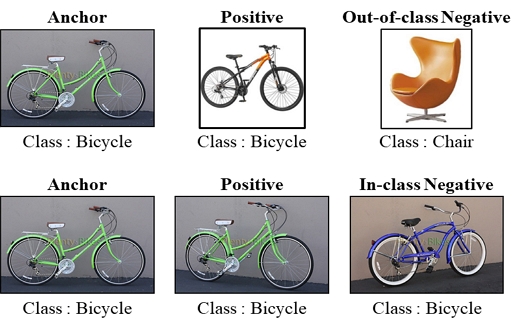
삼중항 손실을 효율적으로 적용하기 위해서는 삼중항을 구성하는 방법이 중요하다. 일반적인 삼중항 샘플링의 경우에 anchor와 동일한 class에 속하는 이미지는 positive 샘플로, 그 외의 class에 속하는 이미지는 negative 샘플로 구성한다. 이러한 삼중항 샘플링은 학습이 진행됨에 따라 이미 상대적 거리가 조정된 결과가 출력되어 학습에 도움이 되지 못하는 문제가 발생한다. 따라서 차이를 구분하기 어려운 샘플이 어느 정도 비율에 따라 구성되어야 한다.

제안하는 방법에서는 어려운 샘플을 구성하기 위해 클래스 정보를 이용한다. 클래스 내부의 이미지 간의 비교는 더 정교한 차이를 학습해야 하므로 클래스 외부 이미지 간의 비교보다는 상대적으로 어렵다. 그래서 삼중항 샘플링을 적용할 때, anchor와 같은 상품 이미지를 positive 샘플로, anchor가 속한 class의 다른 이미지를 negative 샘플로 사용하는 in-class negative 샘플링과 기존과 같이 클래스 외부 이미지를 사용하는 out-of-class negative 샘플링으로 구분하고 각 배치를 4:6 비율로 구성되도록 한다. 이러한 샘플링 전략을 통해 모델에게 더 어려운 구분 문제를 제시하여 학습 효율을 높일 수 있다. 그림 3은 구성되는 샘플링 형태에 따른 삼중항 샘플링의 예시를 보여준다. 그림 4에서 해당 샘플링 방법을 이용해 학습을 진행하였을 때, 각 상품 이미지의 임베딩 벡터가 변화하는 결과를 시각적으로 표현하였다.

Fig. 3.

Examples of triplet sampling by using class information

Fig. 4.

The process of learning the relative position of an embedding vector generated through the Swin Transformer v2 encoder. Triplet sampling is performed by varying the ratio of the probability of selecting a negative sample in-class and out-of-class at 4:6.

3. HNSW 알고리즘

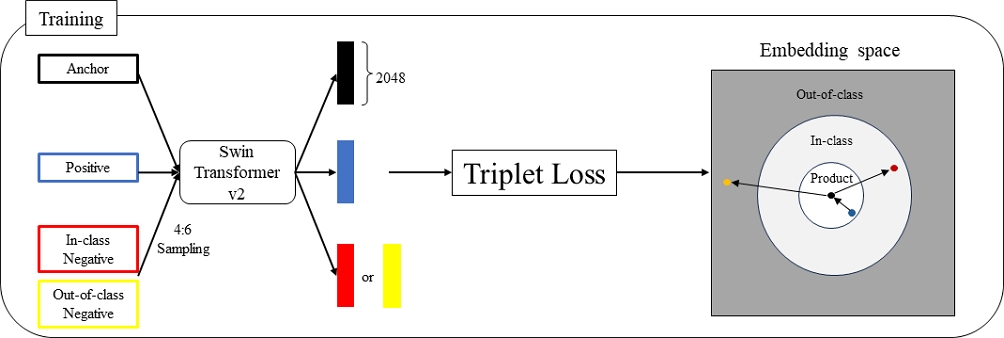
HNSW 알고리즘은 brute force KNN에 비해 훨씬 적은 시간복잡도를 지닌다. 이는 IV장의 실험 결과를 통해 확인할 수 있다. 본 논문에서는 학습이 완료된 Swin Transformer v2 모델을 이용해 SOP 데이터 세트를 임베딩 벡터로 변환한 매트릭스를 저장하고, 새로운 query 이미지를 입력으로 받아 임베딩 벡터로 변환한 후 HNSW 알고리즘을 통해 유사한 이미지 K개의 인덱스를 추출하고 이에 해당하는 상품 이미지를 출력한다. 전체적인 알고리즘의 적용 과정은 그림 5를 통해 확인할 수 있다.

Fig. 5.

Image retrieval process in our method

1. 데이터 세트

제안하는 방법의 성능을 평가하기 위해 SOP(Stanford Online Products) 데이터 세트를 이용한다^[8]. SOP 데이터 세트는 12개의 상품 클래스와 22,634개의 상품으로 구성된다. 상품별로 다른 각도에서 촬영한 여러 장의 이미지로 이루어져 총 120,053장의 상품 이미지로 구성된다. 쇼핑몰의 데이터 형태와 비슷한 구조로 되어 있어 이미지 검색 성능 평가에 적합하다.

2. 모델 평가 지표

모델의 성능 평가는 Recall@K 지표를 사용한다. 각 query 이미지로 검색한 K개의 유사 이미지 안에 query와 같은 제품의 이미지가 검색되는 경우 매칭된 것으로 판단한다. 매칭되는 이미지가 하나라도 있는 경우를 1, 어떠한 이미지도 매칭되지 않았을 경우를 0으로 측정한다. 본 논문에서는 전체 query에 대해 해당 점수의 평균을 낸 평균 Recall@K을 통해 유사도 이미지 검색 성능을 평가한다^[4].

3. 모델 학습 파라미터 및 실험 환경

실험은 NVIDIA V100 그래픽 카드를 사용하여 진행하고, 50 epoch 학습을 진행한다. 학습 파라미터는 다음과 같이 설정한다.

• •Image Size : 256
• •Optimizer : AdamW
• •LR Scheduler : Cosine Annealing
• •Learning Rate : 0.001
• •Triplet Size : 15
• •Margin(α) : 0.5

4. 유사 이미지 검색 성능

성능 평가를 위해 ImageNet 데이터 세트로 사전 학습된 pre-trained 모델, out-of-class만 사용하는 기존의 랜덤 삼중항 샘플링을 학습한 모델, 제안하는 방법의 삼중항 샘플링 기법을 적용한 모델의 성능을 비교한다. 표 1은 제안하는 방법의 유사 이미지 검색 성능을 나타낸다. 실험 결과를 통해 제안하는 방법의 성능이 모든 Recall@K 지표에서 높게 나온 것을 확인할 수 있다. 이는 모델이 더 어려운 구분 문제를 학습함으로써 임베딩 공간에서의 구분 능력이 더 높아진 것으로 판단된다.

Table 1.

Performance of the proposed method with brute force KNN

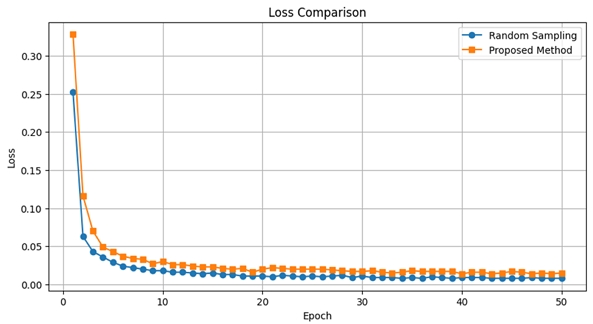
앞선 3.2절에서 구별이 쉬운 데이터만을 사용해 학습에 사용할 때, 상대적 거리를 모델이 빠르게 학습하여 더 이상 훈련이 진행되지 않는 문제가 발생하므로 구별이 더욱 어려운 데이터를 학습시키는 것이 성능의 향상에 영향을 미칠 것이라 가정하였다. 그림 6은 학습을 진행하며 삼중항 손실을 출력한 값이다. 랜덤하게 샘플링한 기존의 방법론의 경우 모델이 더 빠르게 수렴하고 또한 손실값이 더욱 낮다. 하지만, 삼중항 샘플의 구성이 더욱 쉬우므로 이러한 현상이 발생한 것이며, 표 1에서 확인한 바와 같이 제안한 샘플링 방법론을 사용해 학습할 때 더욱 높은 일반화 성능을 기대할 수 있다.

Fig. 6.

Triplet loss in training

최적의 샘플링 비율을 찾기 위해 표 2와 같이 샘플링 비율(in-class : out-of-class)을 달리하였을 때, 성능지표가 어떻게 변화하는지 brute force KNN 알고리즘을 통해 비교하였다. 0:10은 모든 negative 샘플이 out-of-class인 랜덤 샘플링에 해당한다. 이에 비교하여 점차 어려운 데이터의 비율이 증가할수록 성능이 향상하였고, in-class negative와 out-of-class negative 샘플의 비율이 4:6 혹은 5:5일 때 가장 좋은 성능을 보였다.

Table 2.

Performance comparison according to sampling ratio (in-class: out-of-class) using brute force KNN algorithm

그림 7은 기존의 샘플링 방법과 제안한 샘플링 방법으로 학습한 모델에 대하여 같은 클래스인 bicycle 내에서 동일한 상품은 같은 색으로 표현해 5개의 상품을 t-SNE^[9]로 시각화한 결과이다. 붉은 원으로 표시한 내부를 살펴보면 기존의 랜덤하게 샘플링한 방법으로 학습한 모델(좌)은 서로 다른 상품임에도 가장 근접한 임베딩 벡터로 변환하였다. 이에 반하여 클래스 정보를 주어 학습한 모델은 해당 이미지를 적절하게 변환하였다. 그림 8은 그림 7에서 붉은 원으로 감싼 두 임베딩 벡터의 실제 데이터이다. 서로 다른 상품이지만, 자전거의 체인에 해당하는 특징에 집중하여 비슷한 이미지라고 판단하였다고 볼 수 있다. 따라서 클래스에 따라 샘플링하는 본 논문의 전략은 상품 이미지 검색 모델을 학습하는 데에 있어 핵심이 되는 기술이다.

Fig. 7.

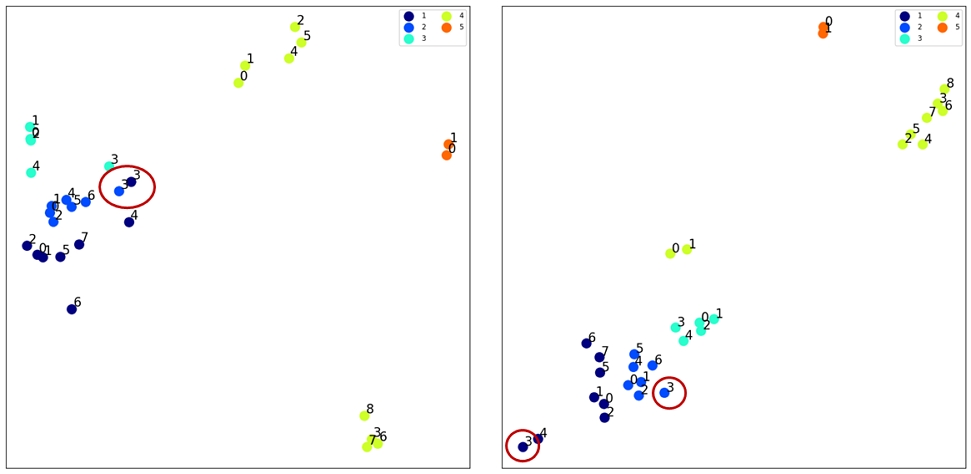
Visualization of 5 products from the bicycle_final dataset using t-SNE for random sampling method (left) and ours (right)

Fig. 8.

The random sampling model reasoned that these two images was very similar, but it’s not

5. 검색 알고리즘 간 성능 비교

각 유사 이미지 검색 알고리즘 간 속도, 정확도, 메모리 요구량을 측정하였다. 학습을 완료한 유사도 검색 모델을 사용하였으며 brute force KNN, ANNOY, HNSW을 적용하여 성능을 비교하였다. 아래의 표 3과 표 4는 총 60,502장의 테스트 데이터 세트에 대해, 제안하는 방법을 이용해 검색할 때 소요되는 시간과 정확도를 나타낸다.

Table 3.

Comparison of speed between ANN algorithms

Table 4.

Comparison of accuracy between ANN algorithms

실험 결과를 통해 제안하는 방법이 가장 빠른 검색 속도를 보이는 것을 확인할 수 있다. Brute force KNN 기법은 특별히 605,020장의 데이터 세트에 대하여 10초 이상의 검색 시간이 소요되었다. 구글 리서치의 조사자료에 따르면, 웹페이지의 로딩 시간이 1초에서 10초로 늘어날 경우, 사용자가 해당 페이지를 이탈할 확률이 123% 증가한다고 한다^[10]. 즉, brute force KNN 기법은 실제 온라인 쇼핑 서비스에 적용하기에 큰 어려움이 예상된다. 이에 비해 HNSW 알고리즘을 적용하면 약 224배 빠른 검색 속도를 보였으며, 실제 서비스 구현에도 크게 영향을 끼치지 않는 수치에 해당한다. 다만, 전체적인 Recall@K 값은 HNSW 알고리즘이 brute force KNN에 비해 다소 감소하였음을 확인할 수 있다. 이는 HNSW 알고리즘의 검색 방식으로 인해 local optima를 찾아냈기 때문이다. 그 이유는 첫째로, 각 계층에서 query와 가장 가까운 데이터를 greedy 알고리즘으로 근사적으로 찾는 과정에서 발생한다. 둘째로, 계층적으로 찾아가는 방법에서도 발생한다. 이전 계층에서 최적의 노드를 놓치면, 이후의 층에서도 최적의 노드를 찾지 못하고 잘못된 경로로 탐색이 이어질 가능성이 높아진다. 마지막으로, 시작점이 랜덤하게 초기화되기 때문에 결과 역시 이에 따라 달라질 수 있다.

실제 서비스에 이용하기 위해 메모리 요구량은 매우 중요한 지표이다. 표 5는 각 알고리즘을 사용하였을 때의 메모리 사용량을 비교한 결과이다. 각 원소는 float32를 기준으로 하였다. brute force KNN는 기존의 임베딩 매트릭스를 이용해 dot product method로 계산하므로 메모리의 크기는 임베딩 매트릭스 전체에 해당한다. 따라서 주어진 데이터의 개수를 이용해 계산할 수 있다. 각 원소가 4바이트에 해당하며 임베딩 벡터의 크기는 2048이므로 이를 통해 간단하게 필요한 메모리의 양을 MB 단위로 계산할 수 있다. HNSW 알고리즘은 이에 더해 인덱스를 생성하고 저장하기 위한 메모리가 요구된다. 이는 주요 파라미터 중 하나인 M의 값에 따라 달라지는데, 각 노드당 M개의 양방향 연결을 통해 그래프를 생성하기 때문이다. 따라서 HNSW 알고리즘의 경우 각 벡터당 2048*4 + M*2*4으로 계산할 수 있다. 표 5는 직접 계산을 통해 요구되는 메모리를 나타내었고, 가장 오른쪽의 열은 파이썬의 psutil 라이브러리를 통해 실제로 인덱스 생성 후 증가하는 메모리를 측정한 결과이다. 1,000,000장의 데이터에 대해 약 8GB에 해당하는 메모리가 필요함을 알 수 있다.

Table 5.

Comparison of memory usage comparison between ANN algorithms

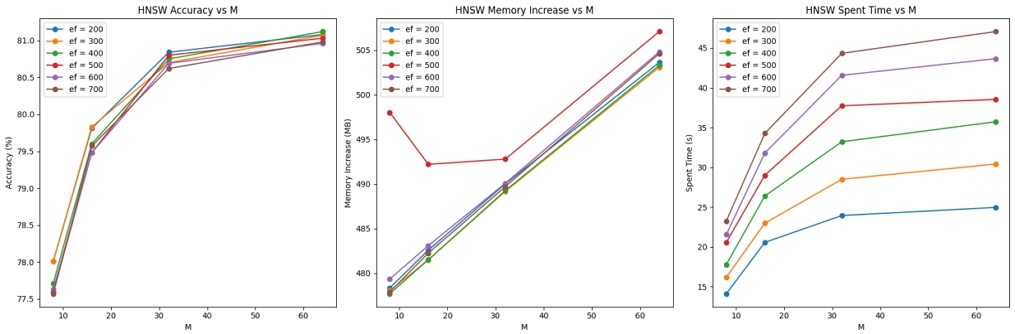
그림 9는 HNSW 알고리즘의 두 파라미터인 ef(검색 시 저장하는 dynamic list의 크기), M(인덱스 생성 시 사용하는 link의 수)에 따라 변화하는 정확도(Recall@1), 메모리 요구량, 소요 시간을 측정한 결과이다. ef가 400, M가 64일 때 가장 성능이 좋으며 메모리와 속도 측면에서 준수한 수치를 기록하므로 해당 방법론을 최종적으로 채택하였다.

Fig. 9.

Performance of HNSW algorithm according to hyperparameters

표 6은 각 샘플링 비율(in-class : out-of-class)에 따라 학습을 완료한 임베딩 벡터에 대해 HNSW 알고리즘을 적용하였을 때 이미지 검색 정확도를 비교한 결과이다. 샘플링 비율이 4:6일 때, 모든 K 값에 대하여 가장 좋은 성능을 보인다. 그러므로 본 논문에서는 제안한 모델의 성능을 비교하기 위하여 샘플링 비율로 4:6을 사용하였다. 표 7은 기존의 삼중항 학습을 사용하여 가장 높은 성능을 보인 방법^[4]과 비교한 결과이다. 그 결과 본 논문에서 제안하는 방법론이 모든 지표에서 좋은 성능을 보인다.

Table 6.

Comparison of accuracy between sampling ratios (in-class : out-of-class) with HNSW algorithm

Table 7.

Comparison of performance between current method