[ Letter Paper ]

JOURNAL OF BROADCAST ENGINEERING - Vol. 30, No. 1, pp.76-79

ISSN: 1226-7953 (Print) 2287-9137 (Online)

Print publication date 31 Jan 2025

Received 14 Nov 2024 Revised 10 Dec 2024 Accepted 11 Dec 2024

DOI: https://doi.org/10.5909/JBE.2025.30.1.76

변환 오디오 부호화를 위한 기계 학습 기반의 시간 영역 신호 제어 기술

김재원^a) ; 유정찬^a) ; 박호종^a)^{, ‡}

a)광운대학교 전자공학과

Time-Domain Signal Control based on Machine Learning for Transform Audio Coding

Jaewon Kim^a) ; Jeongchan Yu^a) ; Hochong Park^a)^{, ‡}

a)Dept. of Electronics Engineering, Kwangwoon Univ.

Correspondence to: ^‡박호종(Hochong Park) E-mail: hcpark@kw.ac.kr Tel: +82-2-940-5104

Copyright © 2025 Korean Institute of Broadcast and Media Engineers. All rights reserved.
“This is an Open-Access article distributed under the terms of the Creative Commons BY-NC-ND (http://creativecommons.org/licenses/by-nc-nd/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited and not altered.”

초록

본 논문에서는 변환 오디오 부호화를 위한 기계 학습 기반의 신호 제어 방법을 제안하고, 그 결과를 시간 영역 평탄화 동작과 비교한다. 입력 신호와 기계 학습으로 결정된 제어 신호를 시간 영역에서 곱한 후 부호화하고, 복호화 후에 제어 신호를 제거하여 출력한다. 학습 단계에서 부호화 과정을 포함한 종단 간 학습을 위해 부호화 동작을 미분 가능 형태로 모델링 한다. 학습을 통해 얻은 최적의 신호 제어 동작이 시간 영역 평탄화에 해당하고 과도 신호 구간에서 성능 향상을 제공하는 것을 확인하였다.

Abstract

This paper proposes a signal control method based on machine learning for transform audio coding and compares the results with time-domain flattening operation. The input signal and the control signal determined by machine learning are multiplied in the time domain before encoding, and the control signal is removed after decoding. In the training stage, the encoding operation is modeled in a differentiable form for end-to-end training. It is confirmed that the optimal signal control corresponds to the time-domain flattening and provides performance improvement in the transient region.

Keywords:

Transform audio coding, Machine learning, Time-domain signal control

Ⅰ. 서 론

변환 오디오 부호화(transform audio coding)는 입력 신호를 주파수 영역으로 변환하여 주파수 계수를 양자화하며, 성능 향상을 위해 주파수 영역 예측, 스펙트럼 포락선 평탄화, 대역폭 확장 등의 도구들이 개발되었다^[1-4]. 최근, 과도 신호(transient signal) 구간에서 프리 에코(pre-echo) 문제를 해결하기 위해 입력 신호의 시간 영역 포락선(temporal envelope)을 적용하여 신호를 평탄화한 후에 부호화하는 방법이 개발되었고 성능 향상이 확인되었다^[5]. 그러나 이 방법은 과도 신호 구간에서의 시간 영역 평탄화라는 미리 정해진 목표에 따라 설계된 동작에 불과하고, 시간 영역 평탄화가 부호화를 위한 최적의 시간 영역 제어인지는 검증하지 못하였다.

본 논문에서는 기계 학습 기반으로 시간 영역에서 입력 신호를 제어하는 방법을 제안하고, 이를 통해 최적의 신호 제어 동작과 [5]의 시간 영역 평탄화와의 관계를 확인하고자 한다. 제안하는 방법은 시간 영역에서 입력 신호와 제어 신호를 곱한 후에 부호화하고, 복호화 후에 제어 신호를 제거하여 최종 출력을 구하는 과정으로 수행되고, 최상의 부호화 성능을 가지도록 기계 학습 기반으로 제어 신호를 구하는 것이 핵심이다.

제안 방법의 개발을 위해 부호화 동작을 포함하여 종단 간(end-to-end) 학습을 수행해야 한다. 즉, 학습 대상인 제어 신호는 부호화 전에 적용되고, 최종 복호화된 신호의 왜곡이 최소가 되도록 학습해야 한다. 그러나 부호화 과정은 미분 불가능하여 역전파(back-propagation)를 그대로 사용할 수 없다. 이를 해결하기 위해 본 논문에서는 학습 단계에서 부호화 왜곡을 곱셈 가우스 잡음(multiplicative Gaussian noise)으로 모델링 하는 방법을 제안한다.

학습을 통해 결정된 최적의 제어 신호가 입력 신호의 시간 영역 포락선과 관련되고, 최적의 신호 제어 동작이 시간 영역 평탄화에 해당하는 것을 확인하였다. 또한, 제안한 신호 제어를 통해 과도 신호 구간에서 부호화 성능이 향상되는 것을 확인하였다.

Ⅱ. 제안하는 신호 제어 방법

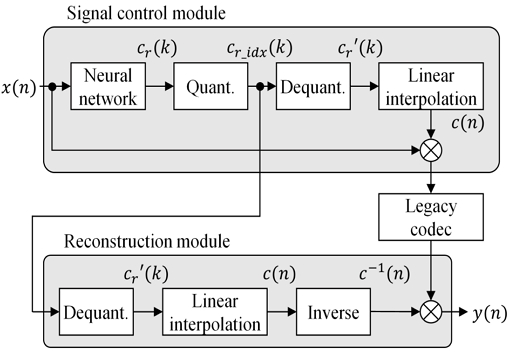
제안하는 방법의 전체 동작 구조는 그림 1과 같다. 신호 제어 모듈(signal control module)에서 신경망을 통해 입력 신호 x(n)으로부터 제어 신호 c(n)을 결정하고 두 신호를 곱하여 x(n)c(n)을 생성하고, 이를 기존 코덱(legacy codec)으로 부호화하여 전송한다. 복원 모듈(reconstruction module)에서는 복호화된 신호에 c^-1(n)을 곱하여 최종 신호 y(n)을 출력한다.

Fig. 1.

Overall structure of the proposed method

신호의 완벽한 복원을 위해 두 모듈에서 동일한 c(n)을 사용해야 하며 이를 위해 해당 정보를 전송해야 한다. 이 때, c(n)을 직접 양자화하면 많은 비트가 필요하므로 제안 방법에서는 한 프레임을 8개의 균일한 시간 구간으로 분할하고 구간별 파라미터를 구하여 양자화한다. 그림 1과 같이 신경망은 x(n)의 구간별 레벨에 해당하는 c_r(k), 0 ≦ k < 8를 출력하고, 이를 양자화하여 복원 모듈로 전송한다. c_r(0)과 c_r(7)은 각 2비트, 나머지 c_r(k)는 각 3비트로 비균등 스칼라(scalar) 양자화하여 총 22비트를 사용하고, 성능 평가에서 사용한 32 kHz 샘플링 주파수와 1024 샘플 프레임을 기준으로 비트율 688 bps에 해당한다. 두 모듈에서 양자화된 c_r′(k)를 각 구간의 중앙값으로 설정하고 샘플 단위로 선형 보간(linear interpolation)하여 c(n)을 정의한다.

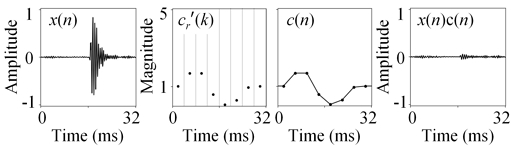
그림 2가 신호 제어 모듈에서의 신호 예를 보여준다. 한 프레임의 x(n)로부터 구간별 c_r(k)를 구하여 양자화된 c_r′(k)를 계산한다. 다음, c_r′(k)를 선형 보간하여 샘플 단위의 c(n)을 계산하고, 마지막으로 x(n)c(n)을 구한다.

Fig. 2.

Example of signal for each step in signal control module

그림 1에서 신경망 학습을 위해 x(n)과 y(n) 사이의 오류를 기반으로 종단 간 학습을 해야 한다. 그러나 부호화의 양자화 동작은 미분할 수 없으므로 그림 1의 legacy codec을 그대로 적용하여 학습을 수행하는 것은 불가능하고, 따라서 해당 동작을 실제 부호화 동작에 따른 학습 결과를 제공할 수 있는 미분 가능 동작으로 대체하여야 한다. 또한, 특정 부호화기 동작에 종속되지 않도록 학습시키기 위해 부호화기의 일반적인 동작만을 학습해야 한다. 이를 위해 본 논문에서는 주파수 영역에서의 양자화 동작을 곱셈 가우스 잡음으로 모델링 하는 방법을 제안한다.

학습 단계에서 x(n)c(n)의 modified discrete cosine transform (MDCT) 계수를 구하고, MDCT 계수에 가우스 잡음을 곱하는 방법으로 양자화 동작을 모델링 한다. 이 동작은 미분 가능하고, 오차가 곱해지므로 MDCT 계수 크기에 따라 가변적인 양자화 오차 크기를 모델링 할 수 있다. 따라서 학습 단계에서는 그림 1의 legacy codec이 MDCT 계수에 대한 잡음 곱하기 동작으로 대체된다. 또한 c_r(k) 양자화는 전송을 위한 것이므로 학습 단계에서는 제거된다. 성능 평가에서 사용하는 부호화 규격과 동일한 신호 대 잡음 비(signal-to-noise ratio, SNR)가 되도록 가우스 잡음의 평균은 1.0, 분산은 0.2로 설정하였다.

변환 부호화는 프레임 단위로 동작하고 제안 방법도 프레임 단위로 c(n)을 구하므로 프레임 사이의 c(n) 연속성을 보장하는 방법이 필요하다. 그림 3이 이 과정의 예를 보여주며, 프레임 단위로 구한 c(n)은 일반적으로 그림 3 (a)와 같이 프레임 사이에서 불연속하다. 제안 방법은 이를 해결하기 위하여 신경망 학습 시 c_r(0)과 c_r(7) 값이 1.0이 되도록 학습 조건을 추가하며, 이 조건을 포함하여 학습하여 c_r(k)을 구하면 그림 3 (b)와 같이 c_r(0)과 c_r(7) 값이 1.0에 근접하게 된다. 마지막으로 그림 3 (b)와 같이 이전 프레임의 마지막 c(n) 값을 현재 프레임 선형 보간의 시작 값으로 설정하고 c(n)을 구하면 불연속 문제가 해결된다.

Fig. 3.

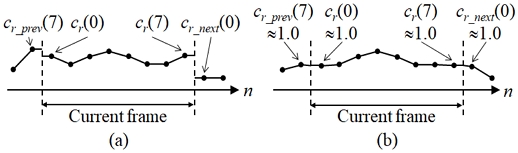
Frame continuity of control signal, (a) discontinuous control signal, (b) continuous control signal after extra training criterion

제안 방법에서 신경망은 6개의 완전 연결 계층(fully connected layer)으로 구성된다. 각 층의 크기(layer dimension)는 1024, 1024, 1024, 64, 32, 8이고, 1024 샘플의 x(n)을 입력 받고 8개의 c_r(k)을 출력한다. 모든 층에서 활성화 함수(activation function)는 rectified linear unit(ReLU)이다.

Ⅲ. 성능 평가

성능 평가를 위한 부호화기는 샘플링 주파수 32 kHz와 비트율 48 kbps의 모노 MPEG-H 3DA-FD로 설정하였고, 윈도우 전환(window switching)은 적용하지 않는다^[4]. 신경망 학습에는 Beethoven piano sonata, VCTK　speech dataset^[6], RWC music dataset^[7]에서 수집한 총 약 57시간 길이의 학습 데이터와 검증(validation) 데이터를 사용하였고, 식 (1)의 손실 함수를 사용하였고, N=1024이다.

L = ∑ n = 0 N - 1 y n - x n 2 + c r 0 - 1.0 2 + c r 7 - 1.0 2

(1)

그림 4는 캐스터네츠 신호(상단)와 음성 신호(하단)에 대하여 세 프레임 길이의 입력 신호, [5]에서 구한 시간 축 포락선, 제안 방법이 구한 최적 제어 신호의 역 c^-1(n)을 보여준다. 이 결과로부터 최적의 제어 신호가 시간 축 포락선과 관련되고, 제안 방법의 x(n)c(n) 동작이 시간 영역에서의 평탄화 과정에 해당하는 것을 알 수 있고, [5]의 방법이 변환 오디오 부호화의 성능 향상을 위한 최적의 시간 영역 신호 제어라는 것을 알 수 있다.

Fig. 4.

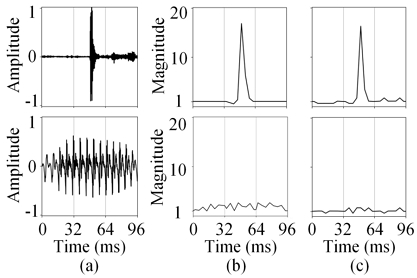
Results of proposed method, (a) input signal, (b) temporal envelope in [5], (c) inverse control signal of proposed method

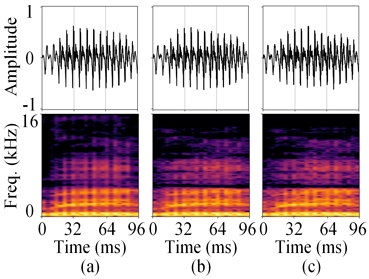
그림 5는 그림 4의 캐스터네츠 신호에 대하여 여러 부호화 방법의 결과를 보여준다. [5] 방법을 적용한 그림 5 (c)와 제안 방법을 적용한 그림 5 (d)에서 프리 에코가 감소되어 3DA-FD에 비하여 부호화 성능이 향상된 것을 확인할 수 있다. 그림 6은 그림 4의 음성 신호에 대한 결과를 보여준다. 이 신호는 정상(stationary) 구간에 해당하고 그림 4 (c) 하단의 c^-1(n)이 평탄하므로 x(n)c(n) 동작을 수행하여도 근본적인 신호 변화가 발생하지 않고 3DA-FD와 동등한 부호화 동작을 수행한다. [5]에서는 별도의 선택 과정으로 과도 신호 구간을 검출하고 시간 영역 평탄화 과정을 수행하지만, 제안 방법은 구간 선택 없이 모든 구간에서 동일한 신호 제어를 수행하고 그에 따라 성능 향상을 얻는 차이점을 가진다.

Fig. 5.

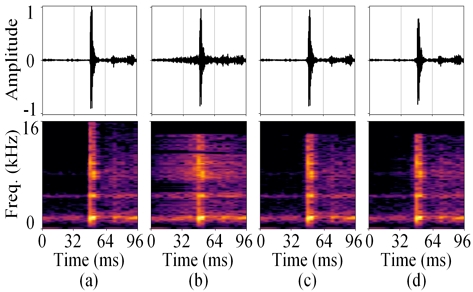
Result of each coding method for castanet signal, (a) original, (b) 3DA-FD, (c) [5] method, (d) proposed method

Fig. 6.

Result of each coding method for speech signal, (a) original, (b) 3DA-FD, (c) proposed method

Ⅳ. 결 론

본 논문에서는 변환 오디오 부호화를 위한 기계 학습 기반의 시간 영역 신호 제어 방법을 제안하였다. 학습 단계에서 부호화 과정을 미분 가능한 동작으로 모델링 하고, 종단 간 학습을 통해 최적의 제어 신호를 구하였다. 학습을 통한 최적 제어 신호가 입력 신호의 시간 축 포락선의 역과 유사함을 확인하였고, 이로부터 기계 학습 기반의 최적 시간 영역 신호 제어 동작이 시간 영역 평탄화에 해당하는 것을 검증하였다.

Acknowledgments

이 논문은 한국전자통신연구원 지원사업(24ZC1100_07, 정보량 감축 오디오 압축 툴 기술 개발)과 2024년도 광운대학교 교내학술연구비 지원을 받아 수행된 연구임.

References

D. Pan, “A tutorial on MPEG/audio compression,” IEEE Multimedia, vol. 2, no. 2, pp. 60-74, 1995. [https://doi.org/10.1109/93.388209]
M. Dietz, L. Liljeryd, K. Kjörling, and O. Kunz, “Spectral band replication, a novel approach in audio coding,” Proc. 112th Audio Eng. Soc. Conv., 2002.
J. Herre and M. Dietz, “MPEG-4 high-efficiency AAC coding,” IEEE Signal Processing Magazine, vol. 25, pp. 137-142, 2008. [https://doi.org/10.1109/MSP.2008.918684]
J. Herre, J. Hilpert, A. Kuntz, and J. Plogsties, “MPEG-H 3D audio – the new standard for coding of immersive spatial audio,” IEEE J. of Selected Topics in Sig. Proc., vol. 9, no. 5, pp. 770-779, 2015. [https://doi.org/10.1109/JSTSP.2015.2411578]
J.-W. Kim, B. Jo, S. Beack, and H. Park, “Pre-echo reduction in transform audio coding via temporal envelope control with machine learning based estimation,” Proc. IEEE Int. Conf. on Acoustics, Speech and Sig. Proc., pp. 536-540, 2024. [https://doi.org/10.1109/ICASSP48485.2024.10448341]
C. Veaux, J. Yamagishi, and K. MacDonald, “Superseded-CSTR VCTK corpus: English multi-speaker corpus for CSTR voice cloning toolkit,” 2016.
M. Goto, “Development of the RWC music database,” Proc. Int. Congress on Acoustics (ICA), pp. I-553-556, April 2004.