LLaMA 3 온디바이스 가속기의 구현을 위한 고정소수점 연산 분석
 ; Seunghwan Yoona)
; Seunghwan Yoona) ; Seongwon Lima)
; Seongwon Lima) ; Sumin Oha)
; Sumin Oha) ; Hakbum Leea)
; Hakbum Leea) ; Minji Leea)
; Minji Leea) ; Dongkyeong Kanga)
; Dongkyeong Kanga) ; Young-Ho Seoa), ‡
; Young-Ho Seoa), ‡
Copyright © 2024 Korean Institute of Broadcast and Media Engineers. All rights reserved.
“This is an Open-Access article distributed under the terms of the Creative Commons BY-NC-ND (http://creativecommons.org/licenses/by-nc-nd/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited and not altered.”
초록
LLM(대규모 언어 모델)은 RNN과 LSTM의 발전된 모델로, 트랜스포머 구조를 갖는다. 트랜스포머는 2017년 ‘Attention Is All You Need’ 논문 이후 발전해 OpenAI GPT-4, Google Gemini Pro 1.5 등 성공적인 LLM이 출시되었다. LLM은 방대한 데이터를 학습하기 위해 고성능 GPU가 필요해 일반적으로 로컬에서 개인 사용자에게 공개되지 않는다. Meta AI의 LLaMA 3는 연구적/상업적 목적으로 사용 가능한 오픈소스로, 8B와 70B 모델로 제공된다. LLaMA 3는 로컬에서 실행 가능하지만, 다중 GPU 환경이 필요하다. 온디바이스 LLM을 구동하려면 양자화와 고정 소수점 연산이 필요하며, 엣지 디바이스에서 부동 소수점 연산은 자원 부담이 크다. 고정 소수점 연산은 빠르지만 표현 범위가 좁아 LLM의 답변 정확도에 영향을 미칠 수 있다. 본 논문은 LLaMA 3 8B 모델의 구조와 연산을 분석하고, 고정 소수점 실험 결과와 하드웨어 자원 사용량을 제시한다.
Abstract
LLM (Large Language Model) is an advanced model for processing sequential data, evolving from RNN and LSTM models, and is based on the transformer architecture. Since the publication of the ‘Attention Is All You Need’ paper in 2017, transformers have continuously developed, leading to successful LLMs such as OpenAI's GPT-4 and Google's Gemini Pro 1.5. LLMs require extensive data training, necessitating high-performance GPUs and prolonged training times, which is why they are typically not available for local use by individual users. Meta AI's LLaMA 3, an open-source model for research and commercial use, is available in 8B and 70B parameter models. While LLaMA 3 can be run locally, it requires a multi-GPU environment. To run LLMs on-device, quantization and fixed-point arithmetic are needed due to the resource constraints of edge devices. Floating-point operations are resource-intensive and challenging for edge devices, though fixed-point operations, while faster, have a narrower range and may affect LLM accuracy. This paper analyzes the structure and operations of the LLaMA 3 8B model, presents fixed-point experiment results, and discusses hardware resource usage.
Keywords:
LLaMA 3, LLM, Accelerator, Fixed-Point, ASICⅠ. 서 론
LLM(대규모 언어 모델)은 기존 순차 데이터를 처리하기 위한 RNN과 LSTM 모델의 발전된 모델로, 트랜스포머의 구조를 갖는다. LLM의 기본이 되는 트랜스포머 구조는, 2017년 ‘Attention Is All You Need’ 논문이 공개된 이후로 지속적으로 발전되고 있으며, 현재 OpenAI의 GPT-4, Google의 Gemini Pro 1.5와 같은 성공적인 LLM들이 출시되고 있다[1-3]. 이러한 LLM은 매우 방대한 양의 데이터를 학습하기 때문에 학습시간이 매우 오래걸리며, 학습을 위한 뛰어난 성능의 GPU(Nvidia H100, A100 등)의 대규모 서버가 필요하다. 이처럼 어렵게 학습이 된 특징 때문에 일반적으로 LLM 모델은 로컬에서 개인 사용자에게 공개가 잘 되지 않고, 또한 학습된 파라미터는 수십, 수백만개의 크기를 가지기 때문에 좋은 로컬 GPU에서 동작하기 어려운 특징이 있다.
한편 Meta AI에서 LLaMA 3라는 LLM을 출시하였다. LLaMA는 Large Language Model Meta AI라는 뜻으로 연구적/상업적 목적으로 사용이 가능한 오픈소스로 사전 훈련된 파라미터와 함께 공개되었다. LLaMA 3는 8B, 70B로 학습된 파라미터 수가 다른 두 가지 모델로 공개되었는데, 70B 모델의 경우 Google의 Gemini Pro 1.5 정도의 성능이며, 8B 모델의 경우 OpenAI의 GPT-3.5 turbo 수준의 성능을 갖는다. LLaMA 3의 경우 오픈소스로 공개되어 있기 때문에 로컬에서 직접 실행이 가능하나, 이 역시 8B, 70B 모델의 크기는 각각 약 15GB, 150GB에 해당하며 다중 GPU 환경이 아니면 모델 구동이 어렵다. 이처럼 LLM 모델은 로컬 환경에서 성능이 좋은 GPU가 있어야만 사용할 수 있으며, LLM 모델을 스마트폰과 같은 엣지 디바이스에서 그대로 동작시키기에는 어려움이 존재한다[5].
온디바이스에서 LLM을 구동하기 위해서 거대한 파라미터를 양자화하고 이를 효율적으로 읽고 쓰는 아키텍쳐로 재설계해야 하며 연산 속도가 빠른 LLM 전용 가속기를 설계해야 한다. 한편 LLM은 대부분 Pytorch나 Tensorflow 등의 딥러닝 프레임 워크를 이용해 학습이 되었고, 내부 연산은 모두 부동소수점 단정밀도나 반정밀도를 사용해 연산이 이루어진다. 이 때문에 기존 LLM과 동일한 답변 정확도를 위해선 온디바이스 연산에서 부동 소수점 연산을 수행해야 하는데, 자원이 극도로 한정된 엣지 디바이스에서는 이러한 부동 소수점 연산 동작이 부담스러울뿐더러 GPU처럼 대규모 부동 소수점 병렬 연산을 수행할 수 없다. 반면 고정 소수점(정수 연산) 연산은 부동 소수점 연산에 비해 매우 빠르며 파이프라이닝이 용이하기 때문에 온디바이스 LLM 가속기를 설계하는 관점에서, 기존 LLM 연산을 부동 소수점 체계에서 고정 소수점 체계로 바꾸는 과정이 필요하게 된다[6-9]. 하지만 수를 표현할 수 있는 범위가 매우 넓은 부동 소수점 체계와 달리 고정 소수점은 그 표현 범위가 좁아, LLM의 답변 정확도가 어떻게 변할지 예측할 수 없다[10-11].
따라서 본 논문의 2장에서는 LLaMA 3 8B 모델의 구조 및 수행되는 연산들을 분석한 뒤, 3장에서 고정소수점 실험 방법을 소개한다. 4장에서 고정소수점 실험의 정량적인 결과와 이에 따른 하드웨어 사용량을 분석하고, 5장에서 결론을 맺는다.
Ⅱ. LLaMA 3
1. LLaMA 3의 소개
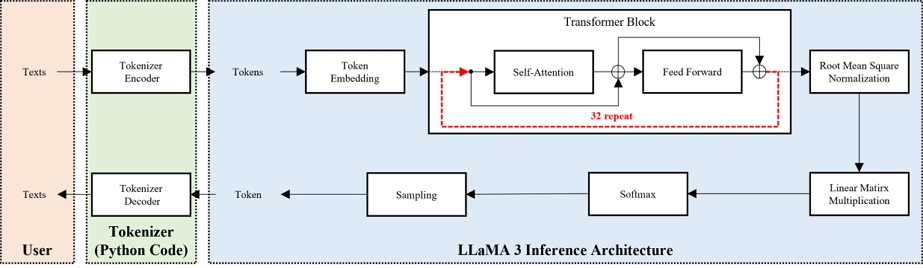
LLaMA 3 모델은 Meta에서 개발한 최신 대형 언어 모델로, 80억(8B) 및 700억(70B) 파라미터의 두 가지 버전으로 제공된다. 이 모델은 최적화된 트랜스포머 아키텍처를 사용하여 뛰어난 처리 능력과 다목적성을 제공하며 특히, 대화 사용 사례에 최적화된 지시 튜닝 버전도 포함하고 있다. LLaMA 3는 확장된 어휘와 토크나이저를 통해 128,000개의 토큰을 지원하여 더 넓고 정밀한 언어적 표현을 가능하게 한다. 이 모델은 15조 개 이상의 토큰으로 훈련되어 LLaMA 2보다 7배 큰 데이터셋을 사용함으로써 더 정교한 이해와 콘텐츠 생성을 실현했다. Meta LLaMA 3는 오픈 소스로 제공되어 개발자, 연구자, 기업이 책임감 있게 생성형 AI 애플리케이션을 구축하고 확장할 수 있게 하였으며, AWS, Google Cloud, Microsoft Azure와 같은 플랫폼과 통합하여 접근성을 높였다. 이를 통해 LLaMA 3는 다양한 산업 분야에서 창의적 콘텐츠 생성 및 고객 서비스 등 여러 응용 프로그램에서 활용될 수 있는 강력한 도구로 자리 잡고 있다. LLaMA 3의 전반적인 구조는 트랜스포머의 디코더만 존재하는 구조를 가지고 있다. 전체적인 구조는 그림 1과 같다.
그림 1과 같이 LLaMA 3는 먼저 사용자의 텍스트 입력으로부터 출발한다. 사용자의 질문에 해당되는 텍스트를 연산에 사용할 수 있게 학습된 정수로 변환하는 과정이 필요하고, 이 과정을 거쳐 나온 정수들을 토큰이라고 한다. 이렇게 변환된 토큰이 LLaMA 3 아키텍쳐에 입력으로 사용되며, 여러 연산을 수행한 뒤, 다시 토큰을 출력하게 된다. 이렇게 출력된 토큰은 다시 각 토큰에 해당되는 텍스트로 변환되어 최종적으로 사용자에게 보여지게 된다.
이 LLaMA 3의 자세한 아키텍쳐가 그림 2에 나타나 있다. LLaMA 3의 입력으로 토큰이 들어가게 되면, 토큰 임베딩이라는 과정을 통해 해당 토큰의 정보가 확장된 학습된 데이터인 고차원의 벡터로 바뀌게 되며, 이 벡터가 트랜스포머 블록으로 입력되게 된다. 이때 정수였던 토큰이 여러 개의 부동소수점의 실수로 변환이 되며 8B 모델의 경우 4096개의 실수로 변환된다. LLaMA 3는 RMSNorm(Root Mean Square Normalization) 과정이 self-attention과 feed-forward 이후가 아닌, 이전에 수행된다. 이렇게 정규화된 데이터는 각각 self-attention과 feedforward로 입력된다. self-attention에서는 입력된 데이터는 사전 학습된 파라미터와 행렬 곱을 통해 각각 Q, K, V로 구분되며, Q와 K에 대해 Position Embedding 과정인 RoPE(Rotary Position Embedding)을 수행한다. 이후 다른 LLM과 같이 softmax 함수가 적용되어 식 (1)과 같이 self-attention이 수행된다.
| (1) |
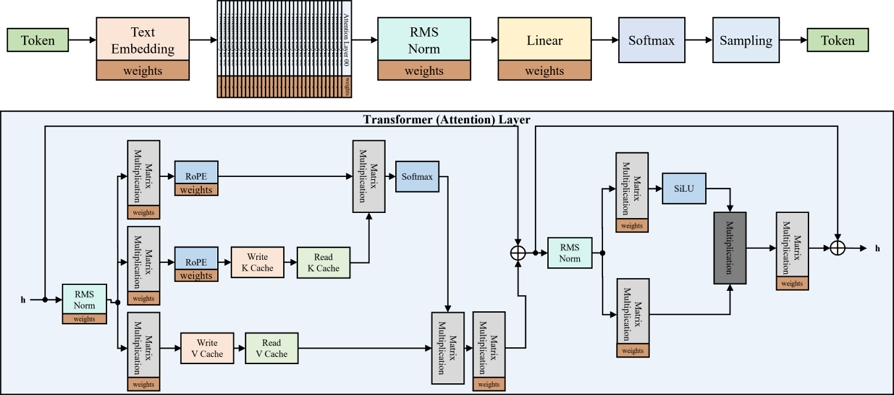
Illustration of the Various Computational Blocks and Internal Structure of Transformer Blocks in LLaMA 3
이때 빠른 학습과 메모리 사용량을 줄이기 위해, Grouped Query Attention이 적용이 되었고, 중간 K, V값은 캐싱을 통해 효율적인 인코더 구조 없이도, 이전 토큰에 대한 정보를 self-attention 과정에서 사용한다. 또한 다른 LLM과 같이 multi-head attention을 수행하기에, 수식 (1)에서 dk는 8B 모델의 경우 4096개의 차원 중 32개의 head를 가져 128의 값을 갖는다. 이후 skip-connetion을 통해 self-attention 결과와 더하고, feedforward 연산을 수행한다. 이때도 역시 RMSNorm이 수행된 후, feedforward 연산을 수행하며 비선형 함수인 SiLU가 사용된다. 이후 이러한 트랜스포머 연산이 여러 번(8B 모델의 경우 32회) 반복되어 최종적으로 다시 RMSNorm 과정을 거친 후, Linear 연산을 통해 표현할 수 있는 토큰의 개수만큼의 벡터(logits)로 변환하여 주고, 이 벡터를 정규분포로 만들어 샘플링하여 다음에 올 토큰 1개를 생성해낸다. 위 과정은 토큰을 1개씩 생성해 낼 때마다 반복되게 되며, LLaMA 3 8B 모델의 경우 파라미터가 약 15GB이므로 토큰 1개를 출력하기 위해 최소 15GB의 파라미터를 연산에 참여시켜야 한다.
한편 대부분의 연산 노드가 부동소수점 반정밀도로 연산을 수행해도 LLM 성능에 변화가 없지만, 그림 2의 RMSNorm과 RoPE, Softmax 과정은 부동소수점 단정밀도로 연산을 수행해야지만 LLM 성능이 유지된다. 이때, LLaMA 3 연산을 고정 소수점 체계로 바꾸는 관점에서, RMSNorm, RoPE, Softmax는 이미 부동소수점 체계에서도 수의 표현 범위에 민감한 것을 알 수 있는데, 고정 소수점 체계로 바꾸었을 때는 이 연산 블록이 표현해야 하는 수의 범위와 정밀도를 표현할 수 있을 정도로의 고정 소수점의 비트 폭과 소수부 비트를 결정해야 할 것이며, LLaMA 3의 정확도를 유지할 수 있게 구현해야 한다.
2. LLM의 평가지표
LLM의 성능을 측정하는 평가지표는 모델의 이해력, 생성 능력, 추론 능력 등을 다양한 방식으로 평가하기 위해 사용된다. 대표적인 평가지표로는 BLEU(Bilingual Evaluation Understudy), ROUGE(Recall-Oriented Understudy for Gisting Evaluation), GLUE(General Language Understanding Evaluation), SuperGLUE, MMLU(Massive Multitask Language Understanding), 그리고 모델의 추론 속도와 메모리 사용량 등이 있다. BLEU와 ROUGE는 주로 기계 번역과 요약 과제에서 모델의 출력과 참조 문장 간의 유사도를 측정하는 데 사용되며, GLUE와 SuperGLUE는 자연어 이해(NLU) 과제를 평가하는 데 사용된다. MMLU는 특히 다양한 분야에서 모델의 전반적인 언어 이해 능력을 평가하는 중요한 지표로, 대규모 멀티태스크 학습 평가를 통해 모델의 지식을 테스트한다.
좀 더 자세히 소개하자면, BLEU는 기계 번역의 품질을 평가하기 위해 개발된 지표로, 생성된 텍스트와 참조 텍스트 간의 n-그램 일치를 측정한다. BLEU 점수는 0에서 1 사이의 값을 가지며, 1에 가까울수록 더 높은 유사성을 의미한다. 이 지표는 텍스트의 길이와 번역의 정확성을 고려하여 평가한다. ROUGE는 주로 텍스트 요약의 품질을 평가하는 데 사용되며, ROUGE-N, ROUGE-L, ROUGE-W 등의 다양한 변형이 있다. 주로 생성된 요약과 참조 요약 간의 중복된 n-그램, 긴 공통 부분, 또는 가중된 길이를 기반으로 평가하며, 요약의 포괄성과 정확성을 측정하는 데 유용하다. GLUE는 자연어 이해(NLU) 모델의 성능을 종합적으로 평가하기 위한 벤치마크로, 문장 유사성, 자연어 추론, 질의 응답 등 다양한 NLU 과제를 포함한다. GLUE 점수는 모델의 전반적인 NLU 능력을 평가하는 데 사용되며, 각 과제에서의 성능을 종합하여 최종 점수를 산출한다. SuperGLUE는 GLUE의 확장판으로, 더 어려운 NLU 과제를 포함하여 모델의 자연어 이해 능력을 더욱 정밀하게 평가한다. SuperGLUE는 단순한 단답형 질문부터 복잡한 추론 문제까지 다양한 과제를 통해 모델의 성능을 평가하며, 기존 GLUE 벤치마크를 뛰어넘는 도전적인 평가를 제공한다.
특히, MMLU는 다양한 주제와 난이도의 57개 과제를 통해 모델의 언어 이해 능력을 평가하는 지표다. MMLU는 문서 이해, 상식 추론, 수학적 추론, 과학, 역사, 법률 등 여러 분야에서 모델이 얼마나 잘 수행하는지를 측정한다. 각 과제는 객관식 질문 형식으로 구성되며, 모델의 답변 정확도를 기반으로 평가된다. MMLU는 특정 도메인에 과도하게 최적화되지 않은 모델의 다목적성과 포괄적인 언어 처리 능력을 평가하는 데 중점을 둔다. 이를 통해 MMLU는 LLM의 전반적인 언어 이해 능력과 실질적인 지식 적용 능력을 평가할 수 있는 강력한 도구로 작용한다. 이러한 평가지표들은 LLM의 다양한 능력을 평가하며, 모델의 전반적인 성능을 종합적으로 이해하는 데 중요한 역할을 한다. MMLU는 특히 다양한 주제와 난이도를 포함한 종합적인 평가를 통해 모델의 다목적성과 포괄적인 성능을 측정하는 데 중요한 역할을 한다.
Ⅲ. 고정소수점 변환
LLaMA 3의 각 연산 블록에서 부동 소수점 연산 체계를 고정 소수점 체계로 변환하는 작업은 가속기 설계에 있어 중요하다. 부동 소수점은 IEEE 표준으로, 부호 비트와 지수부, 가수부 비트가 구분되어 있어 절대값이 매우 큰 수나 매우 작은 수를 표현하는 것이 가능하다. x라는 수가 부동 소수점으로 표현되어 있다면, 부동 소수점의 부호를 s, 지수부 값을 E, 가수부 값을 F라고 할 때, x는 다음과 같이 나타난다.
| (2) |
식 (2)는 부동 소수점 수를 나타내는 기본적인 식이며, subnormal이나 NaN은 고려하지 않았다. LLaMA 3의 연산 노드와 학습된 파라미터들은 기본적으로 부동 소수점 수 체계를 따르며, 이들간의 연산을 위해서는, 연산을 수행할 프로세서 내부의 FPU(Floating Point Unit)의 도움을 받아야 한다. 부동 소수점은 고정 소수점과 달리, NaN, subnormal, inf 등의 예외처리를 해주어야 하며, 모든 연산마다 가수부의 비트를 조절해야 하기 때문이다. 따라서 일반적으로 고정 소수점 (정수)연산보다, 부동 소수점 연산이 오래 걸린다.
하드웨어 가속기 설계의 관점에서 빠른 연산 속도를 달성하기 위해서 LLaMA 3의 수행되는 연산을 부동 소수점 체계에서 고정 소수점 체계로 바꾸어야 한다. 고정 소수점은 정수부와 소수부로 나뉘어져 있다. 정수부 비트 수가 많아짐에 따라 표현 가능한 수의 범위가 넓어지게 되고, 소수부의 비트 수가 많아짐에 따라 표현 가능한 정밀도가 높아지게 된다. 설계에 있어서, 비트 수를 무한정 늘릴 수 없기 때문에, LLaMA 3의 부동 소수점 연산시의 정확도를 유지하면서, 조금씩 비트수를 제한해 가며 고정 소수점 체계의 수로 바꾸며 실험하는 과정이 필요하다.
한편, 일반적인 프로세서에서는 고정 소수점 형식을 지원하지 않으며 실수의 연산은 부동 소수점연산으로 수행할 수 밖에 없다. 따라서 고정 소수점으로 표현되는 데이터를 부동 소수점 형식에 담아 FPU를 이용해 실험을 수행해야 한다. 이러한 실험을 고정 소수점 실험이라고 하며 부동 소수점을 xfloat, 변환된 고정 소수점을 xfixed라고 하고, 고정 소수점의 크기의 최대값을 Mmax, 최솟값을 Mmin, 정수부 비트 길이를 il, 소수부 비트 길이를 fl라고 하면 xfixed는 다음과 같이 나타난다.
| (3) |
| (4) |
식 (5)에서 고정 소수점의 xfloat에 2fl만큼 곱해준 뒤, 가장 가까운 정수로 반올림 한다. 이때 반올림 결과가 변환하고자 하는 고정 소수점의 표현 범위 밖에 존재하는 것을 방지하기 위해 max와 min함수로 각각 정수 비트를 이용해 계산한 식 (3), (4)를 이용해 범위를 제한해준다. 위 방법을 이용해 LLaMA 3의 모든 연산 노드에 식 (5)를 적용하여 고정 소수점의 비트 수를 조절함에 따라 달라지는 LLaMA 3의 정확도 변화를 비교할 수 있다.
| (5) |
Ⅳ. 실험결과
1. 실험 환경
본 논문에서는 LLaMA 3 8B 모델의 부동소수점 데이터를 고정 소수점으로 바꾸어 이에 따른 LLaMA 3의 정확도 변화를 측정하였다. 실험 환경은 Intel(R) Xeon(R) Gold 6338 CPU, Single-Nvidia A100이며 LLaMA 3의 정확도는 MMLU를 측정하여 이용했다. 이때, MMLU 테스트 데이터셋 중 의학 유전학(medical genetics) 분야에 대한 테스트를 수행했다. 의학 유전학 분야의 문제는 4지 선다형으로 100문제가 존재하며, HELM 방식을 이용하여 채점하였고, 모두 1-shot으로 테스트 되었다. 1-shot과 MMLU 질문을 함께 LLaMA 3에 입력한 뒤, 출력되는 첫 토큰만을 채점하여 맞으면 1점, 틀리면 0점으로 환산하며, 의학 유전학 분야의 경우 100문제이기 때문에, 만점은 100점이다.
실험은 다음 순서로 진행되었다. 먼저, 고정 소수점 변환을 하지 않고, PyTorch 프레임워크가 지원하는 연산자로 MMLU 측정을 하여, 기본 모델에 대한 점수를 측정한다. 이 점수가 기준이 되어 고정 소수점 시뮬레이션을 진행한다. 고정 소수점 실험은 두 가지 실험을 수행했는데, 변환할 고정 소수점의 전체 비트 수를 미리 결정하여 모든 연산 노드에서 QPyTorch를 이용해 고정 소수점 시뮬레이션을 진행하여 MMLU 측정을 하는 실험과, 부동 소수점 모델의 점수를 최대한 유지해가며 3장에서 소개한 방법으로 소수부 비트 길이와 정수부 비트 길이를 각각 따로 고정 소수점 시뮬레이션을 수행하는 실험을 수행했다. 또한 LLaMA 3에서 덧셈기와 곱셈기의 하드웨어 양을 비교함으로 어떤 방법이 효율적인지 확인한다.
2. 기존 부동 소수점 추론 결과
먼저 고정 소수점 변환을 하지 않은 기본 부동 소수점 2배 정밀도, 단정밀도, 반정밀도와 bfloat16 데이터 타입에서 테스트한 MMLU(medical genetics)의 점수를 표 1에 정하였다.
부동 소수점을 이용하는 모든 데이터 타입이 82점으로 동일하게 나온 것을 확인할 수 있고, 이 82점이라는 점수가 고정 소수점 실험에서 정확도의 판단 기준이 된다.
3. QPytorch 고정 소수점 실험 결과
고정 소수점 실험의 첫 번째 실험은 QPyTorch라는 파이썬 라이브러리를 사용하였다[12]. QPyTorch 라이브러리는 3장에 소개한 고정 소수점 변환 연산이 구현되어 있다. 이 경우 수식 (3)과 같이 min함수와 max함수가 동시에 적용이 되므로, 고정 소수점의 전체 비트 길이를 정한 후, 사용해야 한다. QPytorch 고정소수점 변환 모듈은 크게 3가지로 생성하였으며 이를 <전체 비트, 소수부 비트>로 표현하면, 각각 <16, N>, <32, 24>, <36, 24>로 구성하였다. <32, 24>, <36, 24>의 고정 소수점 변환 모듈은 LLaMA 3 연산 블록에서 매우 작은 수와 큰 수가 동시에 존재하는 모듈인 RMSNorm과 Softmax 부분에 고정적으로 적용하였고, 나머지 연산 블록은 소수부 비트 길이인 N을 1부터 15비트까지 <16, N> 고정소수점 변환 모듈을 적용하였다.
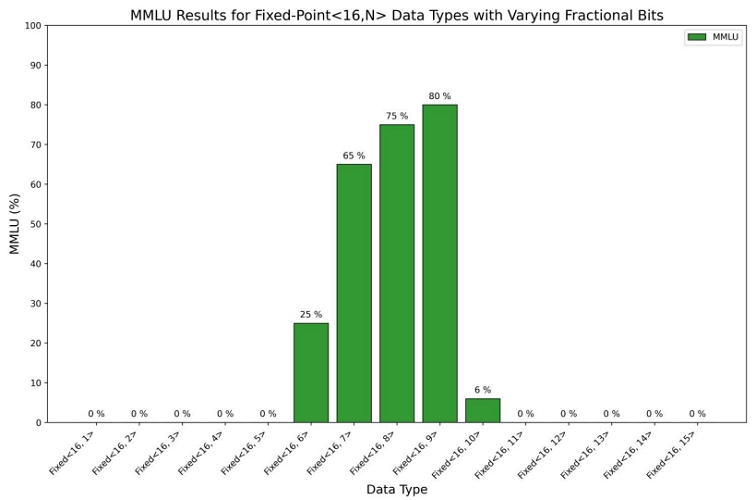
이렇게 3가지 변환 모듈을 고정 소수점 변환을 수행하여 MMLU를 측정한 결과는 표 2와 같다.
실험 결과 표 2와 그림 3과 같이 소수부가 9비트인 <16, 9>체계에서 모델의 정확도가 고정소수점 변환 전인 82점 보다 2점 낮은 80점으로 최대값을 갖게 되며, 소수부가 9비트 보다 작은 경우 모델의 정확도가 낮아지는 것을 확인할 수 있다. 한편, 소수부가 9비트보다 많아질 경우, 정수부 비트가 감소함에 따라 표현할 수 있는 수의 범위가 줄어든다. 이 경우, 모델의 정확도가 급격하게 낮아짐을 알 수 있다. 이것은 적어도 고정 소수점 <16, N>에서 N이 9인 경우 정수부가 7이 되므로, –64와 63사이의 데이터가 표현이 되어야, 모델의 정확도가 80점 선에서 유지되는 것을 알 수 있다.
4. MMLU를 유지하는 고정 소수점 실험 결과
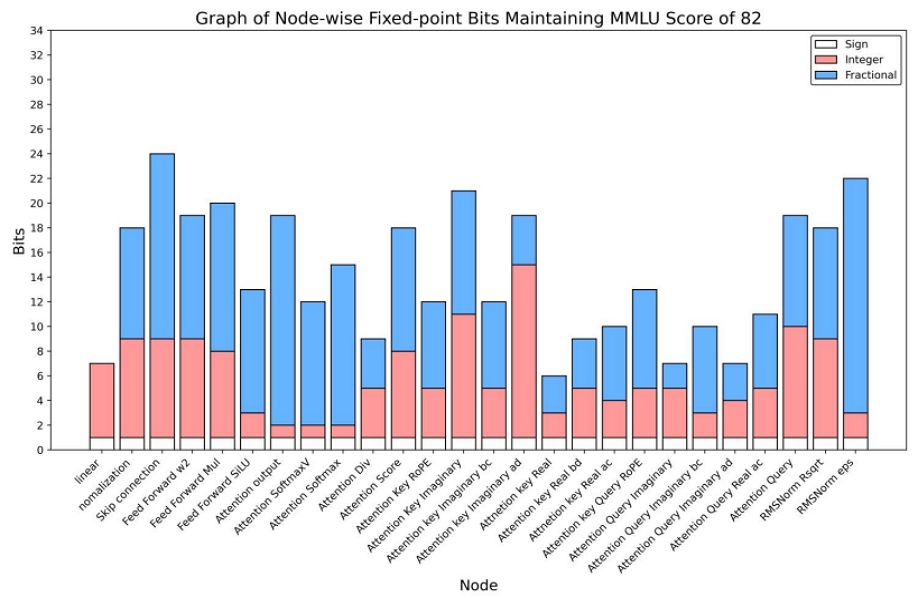
부동 소수점 모델의 MMLU 점수인 82점을 유지하며 최적의 정수/소수부 비트를 찾는 시뮬레이션을 진행하였다. 이 과정은 정수부, 소수부 비트 시뮬레이션을 따로 진행하였다. 수식 (3)을 변형하여 소수부 실험의 경우에는 min/max함수를 적용하지 않고 수행하였고, 정수부 실험의 경우 원본 입력에 min/max함수만을 적용하여 수행할 수 있다. 총 연산 노드 26개에서 최적의 고정 소수점 비트 수를 찾는 실험을 수행했으며, 그 결과가 표 3과 그림 4에 나타나있다.
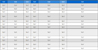
Simulation Results of Optimal Fixed-Point Integer/Fractional Bits per Node Maintaining MMLU Score of 82
그림 4에서 부호비트 1비트를 추가로 고려하여 표시해두었다. 시뮬에이션 상에서는 il이 정수부 비트 길이라고 할 때, 2il - 1또는 –2-il로 clamping이 될 것이지만, 이것은 2의 보수 체계를 이용하기 때문에 결국 고정 소수점에서 사용하는 2의 보수를 위한 부호비트 1비트를 고려해주어야 한다. 시뮬레이션 결과 노드 별로 필요한 정수부와 소수부의 비트수가 상이하지만, 해당 연산 노드에서 고정 소수점의 비트수를 확보해주면, MMLU 점수가 82점으로 유지되는 것을 알 수 있다. 이 경우 QPyTorch 실험과 달리 MMLU 점수가 유지될 수 있지만, 연산블록마다 다른 비트를 사용하는 연산 블록이 사용되어야 할 것이다.
5. 하드웨어 양 측정 결과
LLaMA 3의 연산을 구현하기 위해 각 노드별 필요한 덧셈기 및 곱셈기는 표 4와 같다. 트랜스포머 블록이 LLaMA 3 8B 모델의 경우 32회 반복되기 때문에, 전체적으로 18개의 덧셈기와 22개의 곱셈기가 필요하다. 표 5에 16bit, 24bit, 32bit의 각 덧셈기와 곱셈기가 가지는 게이트 수를 정리하였다. 고정 소수점 연산의 경우 최대 비트수에 따라 연산기가 정해지므로 표 5의 게이트 수와 표 4의 각 노드별 필요한 연산기 수를 기준으로 최대 MMLU를 유지하는 연산기를 분석하였다. 표 6에는 표 4를 기반으로 LLaMA 3 8B에서 사용되는 전체 덧셈기, 곱셈기를 고정소수점 32bit를 사용했을 때를 기준으로 다른 고정 소수점 비트 길이를 사용하는 연산기의 개수의 비율을 나타냈다. 고정 소수점 16bit 연산기를 사용한 경우 32bit 연산기 대비 25~27% 정도의 비율만큼 하드웨어를 사용하지만, MMLU는 2점 낮은 80점이다. 한편 그림 4와 같이 노드 별 여러 고정 소수점 변환 모듈을 이용한 경우 최대 32bit 연산기 대비 51~52%의 하드웨어를 사용하면서 MMLU를 유지하도록 비트 수를 결정했기 MMLU는 최대값인 82점이다. 결과적으로 고정 소수점 실험을 통해 적은 하드웨어 사용량을 달성하면서도 MMLU를 유지하며 모델의 정확도 저하 없이 가속기를 설계할 수 있다.

The number of adders and multipliers required per node in the computational blocks of the LLaMA 3 8B model
Ⅴ. 결 론
본 논문에서는 LLaMA 3 8B 모델의 기존의 부동 소수점 연산 대신 고정 소수점 연산을 사용하는 LLM 가속기를 설계하기 위한 연산 구조를 분석한 뒤, 각 연산 노드별 고정 소수점 시뮬레이션을 수행한 결과를 분석했다. 실험 결과 여러 연산 노드별 고정 소수점을 달리하여 연산기를 설계한다면 MMLU를 충분히 유지하면서도 효율적인 하드웨어 사용량을 가질 수 있음을 확인했다. 하지만 연산 노드별 정수/소수부가 다른 연산기를 설계하면, 부가적인 컨트롤 유닛이 필요할 것이므로 그 균형을 잘 맞추어 설계해야 할 것이다.
Acknowledgments
본 연구는 IDEC에서 EDA Tool의 지원과 과학기술정보통신부 및 정보통신기획평가원의 대학ICT연구센터육성지원사업의 연구결과로 수행되었으며(IITP-2023-RS-2022-00156225), 서울시 산학연 협력사업 2023년 인공지능 기술사업화 지원사업(CY230030)의 지원을 받아 수행된 연구임.
References
-
A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, ... & I. Polosukhin, “Attention is all you need,” Proceeding of Advances in Neural Information Processing Systems (NeurIPS), vol. 30, 2017.
[https://doi.org/10.48550/arXiv.1706.03762]

-
J. Gallifant, A. Fiske, Y. A. Levites Strekalova, J. S. Osorio-Valencia, R. Parke, R. Mwavu, ... & R. Pierce, “Peer review of GPT-4 technical report and systems card,” PLOS Digital Health, vol. 3, no. 1, p. e0000417, 2024.
[https://doi.org/10.1371/journal.pdig.0000417]

-
M. M. Carlà, G. Gambini, A. Baldascino, F. Giannuzzi, F. Boselli, E. Crincoli, ... & S. Rizzo, “Exploring AI-chatbots’ capability to suggest surgical planning in ophthalmology: ChatGPT versus Google Gemini analysis of retinal detachment cases,” British Journal of Ophthalmology, 2024.
[https://doi.org/10.1136/bjo-2023-325143]

-
P. Ersoy, & M. Erşahin, “Benchmarking Llama 3 70B for Code Generation: A Comprehensive Evaluation,” Orclever Proceedings of Research and Development, vol. 4, no. 1, pp. 52-58, 2024.
[https://doi.org/10.56038/oprd.v4i1.444]

-
B. Kim, S. Cha, S. Park, J. Lee, S. Lee, S. H. Kang, ... & K. Sohn, “The Breakthrough Memory Solutions for Improved Performance on LLM Inference,” IEEE Micro, 2024.
[https://doi.org/10.1109/MM.2024.3375352]

-
C. Lai, Z. Zhou, A. Poptani, & W. Zhang, “LCM: LLM-focused Hybrid SPM-cache Architecture with Cache Management for Multi-Core AI Accelerators,” Proceedings of the 38th ACM International Conference on Supercomputing, pp. 62-73, May 2024.
[https://doi.org/10.1145/3650200.3656592]

-
C. H. Yu, H. E. Kim, S. Shin, K. Bong, H. Kim, Y. Boo, ... & J. Oh, “2.4 ATOMUS: A 5nm 32TFLOPS/128TOPS ML System-on-Chip for Latency Critical Applications,” Proceedings of the 2024 IEEE International Solid-State Circuits Conference (ISSCC), vol. 67, pp. 42-44, Feb. 2024. IEEE.
[https://doi.org/10.1109/ISSCC49657.2024.10454509]

-
Y. Fu, Y. Zhang, Z. Yu, S. Li, Z. Ye, C. Li, ... & Y. C. Lin, “Gpt4aigchip: Towards next-generation ai accelerator design automation via large language models,” Proceedings of the 2023 IEEE/ACM International Conference on Computer Aided Design (ICCAD), pp. 1-9, Oct. 2023.
[https://doi.org/10.1109/ICCAD57390.2023.10323953]

-
H. Chen, J. Zhang, Y. Du, S. Xiang, Z. Yue, N. Zhang, ... & Z. Zhang, “A comprehensive evaluation of FPGA-based spatial acceleration of LLMs,” Proceedings of the 2024 ACM/SIGDA International Symposium on Field Programmable Gate Arrays, pp. 185-185, Apr. 2024.
[https://doi.org/10.1145/3626202.3637600]

-
M. Fasi, & M. Mikaitis, “CPFloat: AC library for simulating low-precision arithmetic,” ACM Transactions on Mathematical Software, vol. 49, no. 2, pp. 1-32, 2023.
[https://doi.org/10.1145/3585515]

-
Z. Zhu, A. B. Klein, G. Li, & S. Pang, “Fixed-point iterative linear inverse solver with extended precision,” Scientific Reports, vol. 13, no. 1, p. 5198, 2023.
[https://doi.org/10.1038/s41598-023-32338-5]

-
T. Zhang, Z. Lin, G. Yang, & C. De Sa, “Qpytorch: A low-precision arithmetic simulation framework,” Proceedings of the 2019 Fifth Workshop on Energy Efficient Machine Learning and Cognitive Computing-NeurIPS Edition (EMC2-NIPS), pp. 10-13, Dec. 2019. IEEE.
[https://doi.org/10.1109/EMC2-NIPS53020.2019.00010]


- 2024년 2월 : 광운대학교 전자재료공학과 졸업(공학사)
- 2024년 3월 ~ 현재 : 광운대학교 전자재료공학과 일반대학원(석사과정)
- ORCID : https://orcid.org/0009-0003-0913-0709
- 주관심분야 : 하드웨어 설계, 딥러닝, 3D 영상 처리

- 2019년 3월 ~ 현재 : 광운대학교 전자재료공학과(학사과정)
- ORCID : https://orcid.org/0009-0004-2066-6376
- 주관심분야 : 하드웨어 설계, 딥러닝, 영상 코덱

- 2024년 2월 : 광운대학교 전자재료공학과학과 졸업
- 2024년 3월 ~ 현재 : 광운대학교 전자재료공학과(석사과정)
- ORCID : https://orcid.org/0009-0002-2713-6672
- 주관심분야 : NPU 설계, 홀로그램 코덱

- 2025년 2월 : 광운대학교 전자재료공학과(학사과정)
- ORCID : https://orcid.org/0009-0008-9583-5399
- 주관심분야 : 하드웨어 설계, NPU 가속기 설계

- 2024년 2월 : 광운대학교 전자재료공학과학과 졸업
- 2024년 3월 ~ 현재 : 광운대학교 전자재료공학과(석사과정)
- ORCID : https://orcid.org/0000-0003-0721-4944
- 주관심분야 : 다중 카메라 Calibration, 3D 휴먼 모션 재구성, NPU설계

- 광운대학교 전자재료공학과(학사과정)
- ORCID : https://orcid.org/0009-0005-1173-9809
- 주관심분야 : AI 가속기 설계, 인메모리 컴퓨팅

- 2023년 9월 : 광운대학교 전자재료공학과(석사과정)
- ORCID : https://orcid.org/0009-0006-9627-7734
- 주관심분야 : 하드웨어 설계, Dram MMS 설계, FPGA 검증

- 1999년 2월 : 광운대학교 전자재료공학과 졸업(공학사)
- 2001년 2월 : 광운대학교 일반대학원 졸업(공학석사)
- 2004년 8월 : 광운대학교 일반대학원 졸업(공학박사)
- 2005년 9월 ~ 2008년 2월 : 한성대학교 조교수
- 2008년 3월 ~ 현재 : 광운대학교 전자재료공학과 교수
- ORCID : https://orcid.org/0000-0003-1046-395X
- 주관심분야 : 실감미디어, 2D/3D 영상 신호처리, SoC 설계, 디지털 홀로그램