신경망 기반 블록 단위 위상 홀로그램 이미지 압축
Copyright © 2023, The Korean Institute of Broadcast and Media Engineers
This is an Open-Access article distributed under the terms of the Creative Commons BY-NC-ND (http://creativecommons.org/licenses/by-nc-nd/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited and not altered.
초록
방대한 홀로그램 데이터를 디지털 형식으로 압축하는 것은 중요한 문제이다. 특히, 상용화를 위해 위상 전용 홀로그램의 압축에 관한 연구가 주목된다. 자연 영상에 최적화된 기존 표준 압축 기술은 위상 신호를 압축하는데 적합하지 않으며, 위상 신호에 대해 최적화 가능한 신경망 기반 압축 기술은 좋은 성능을 기대할 수 있으나 고해상도 홀로그램 데이터를 학습하는 데 메모리 문제가 존재한다. 본 논문에서는 메모리 문제를 해결할 수 있는 학습 가능한 신경망 기반의 블록 단위 압축 기술을 위상 전용 홀로그램에 적용해봄으로써 블록 기반이라는 동일 조건 내에서도 제안 방식이 표준 코덱보다 상당한 성능향상을 보일 수 있음을 밝혔다. 신경망 기반의 블록 단위 압축은 기존 코덱과의 호환성을 제공할 수 있으며, 메모리 문제를 해결하는 동시에 위상 전용 홀로그램 압축에 대해 월등히 좋은 성능을 보일 수 있다
Abstract
It is an important issue to compress huge holographic data in a digital format. In particular, research on the compression of phase-only holograms for commercialization is noteworthy. Conventional video coding standards optimized for natural images are not suitable for compressing phase signals, and neural network-based compression model that can be optimized for phase signals can achieve high performance, but has a memory issue in learning high-resolution holographic data. In this paper, we show that by applying a block-based learned image compression model that can solve memory problems to phase-only holograms, the proposed method can demonstrate significant performance improvement over standard codecs even under the same conditions as block-based. Block-based learned compression model can provide compatibility with conventional standard codecs, solve memory problems, and can perform significantly better against phase-only hologram compression.
Keywords:
Phase Only Hologram, Block-based Image Compression, Learned Image Compression, Hologram CompressionⅠ. 서 론
디지털 홀로그래피는 빛의 위상과 세기를 동시에 기록함으로써 복잡한 3D 정보를 기록하고 재구성할 수 있는 차세대 이미지 기술이다. 디지털 홀로그램은 넓은 시야각을 제공하기 위해 다소 작은 단위의 픽셀 크기가 요구되며 하나의 홀로그램에는 대량의 픽셀 수가 포함될 수 있다. 따라서 홀로그램을 기록할 때 발생 되는 상당한 저장 비용과 대역폭 문제를 해결하기 위한 효율적인 홀로그램 압축 방식이 필요하다[1].
디지털 홀로그램은 복소 데이터로 진폭(Amplitude)과 위상(Phase) 혹은 실수(Real)와 허수(Imaginary)의 2D 이미지 조합으로 표현될 수 있다[1]. 홀로그램 데이터는 특수 광 변조기(SLM)에 의해 변조될 수 있으며, 현재 일반적으로 사용되는 SLM은 진폭 또는 위상 신호만 변조할 수 있다. 특히, 위상 변조 방식은 진폭 변조 방식보다 광 효율이 높고, DC, Twin 이미지가 발생하지 않기 때문에 주로 사용된다[2]. 그러나 대부분의 기존 디지털 홀로그램 압축 연구는 실수와 허수 표현의 복소 홀로그램 압축에 대한 것으로 상용화에 적합하지 않다. 따라서 실제 상용화를 위해서는 위상 전용 홀로그램(POH, Phase Only Hologram) 압축을 위한 연구가 필요한 실정이다.
2014년 JPEG는 홀로그램 압축을 위한 JPEG Pleno holography[3]를 포함하는 JPEG Pleno라는 새로운 3D 이미지 압축 표준화 프로젝트를 시작했다. JPEG Pleno에서는 실수와 허수 표현의 복소 홀로그램 압축에 대해 JPEG[4], JPEG 2000[5], H.264/AVC[6], H.265/HEVC[7]의 기존 이미지 및 비디오 코딩 표준을 사용한 사전 압축 실험을 진행했다. 기존의 표준 압축 기술은 자연 영상에 최적화되어 있어 홀로그램 압축 성능에 한계를 보였다. 복소 홀로그램 압축을 위한 Interfere Codec[8]도 개발되어 기존 표준 코덱 대비 높은 성능 향상을 보였지만 이는 복소 홀로그램에 대한 압축 기술로 POH에 적용하는 연구는 부족하다.
한편, 최근에는 POH 압축을 위한 연구들도 진행되고 있다. [9]는 JPEG으로 압축 복원된 POH의 아티팩트를 신경망 학습을 통해 줄이는 후처리 방법을 제안하였다. 또한 랜덤 위상 최적화를 시도한 [10]과 신경망 기반 POH 압축 방법[11,12]도 제안되었다. 딥러닝 기반의 압축 방식은 높은 압축 효율을 보였지만, 큰 해상도의 홀로그램 데이터를 학습하기 위해 매우 큰 메모리가 필요하다는 물리적 어려움이 존재한다.
본 논문에서는 학습 가능한 신경망 기반의 블록 단위 POH 압축 방법이 기존의 표준 비디오 코딩 방법보다 높은 압축 성능을 달성할 수 있음을 밝히고자 한다. 2장에서는 POH의 생성 방법과 기존 압축 기술에 대해 제시한다. 3장에서는 POH를 위한 신경망 기반 블록 단위 압축 방법을 제시한다. 제안 방법은 학습 가능한 신경망 기반 블록 단위 이미지 압축 모델을 사용함으로써 메모리 문제를 해결하고 표준 코덱 간의 호환성을 제공할 수 있다. 4장에서는 제안 방법과 기존 기술의 압축 성능 결과를 비교한다. 4장의 실험 결과를 통해 알 수 있듯, 제안 방법은 최신 비디오 압축 표준인 VVC 대비 BD-rate –48.5%의 상당히 향상된 성능을 보여준다.
Ⅱ. 관련 연구
1. 위상 전용 홀로그램 생성
POH는 복소 데이터인 홀로그램으로부터 위상 정보만을 갖도록 생성된 홀로그램으로 위상 변조 방식에 사용된다. POH는 생성과정에서 진폭 정보의 누락으로 재구성 품질 저하가 발생하는데, 이를 최소화하려는 방법으로 반복적, 비반복적 최적화 기술이 사용될 수 있다. Gerchberg-Saxton (GS) 알고리즘은 대표적인 반복 최적화 방법으로 위상 전용 홀로그램을 생성하는 고전적인 접근 방식이다[13]. Double Phase Amplitude Coding (DPAC)은 진폭과 위상값을 두 위상값으로 인코딩하여 두 위상을 격자 모양의 패턴으로 배치하는 생성기술이다[14]. 이는 비반복적 최적화 기술의 하나로 물리적 이론에 기반을 두며, 다른 반복적 기술 대비 빠른 생성 속도로 사용에 용이하다는 장점이 있다. [15]는 Stochastic Gradient Descent (SGD) 방식을 이용한 반복 최적화 기반의 위상 홀로그램을 생성 방식을 제안했다. SGD 알고리즘은 기존의 알고리즘들보다 좋은 복원화질을 보였지만 최적화까지 많은 시간이 요구된다는 단점이 있다. 본 논문에서는 고전적인 방식의 GS 알고리즘보다 좋은 복원 화질을 가지면서도[15] 빠른 생성 시간으로 널리 사용될 수 있는 DPAC 알고리즘으로 생성된 POH를 실험 대상으로 한다.
DPAC은 이중 위상 방법[16]의 이론에 기반한 방식이다. 이중 위상 방법은 복소 홀로그램의 진폭과 위상 신호를 두 위상 신호로 변환하여 POH를 생성하는 방법이다. 복소 홀로그램 C가 [0,1] 범위를 갖는 진폭 A, 위상 P로 표현될 때, C는 식 (1)과 같이 두 위상 Pa,Pb로 표현 가능하다. 이때 두 항의 위상은 가변적이지만 진폭은 일정한 값을 가진다.
이중 위상 방법에서는 이를 디스플레이할 때 두 위상이 하나의 복소수 값이 되도록 물리적 통합을 용이하게 하기 위해 두 위상을 광학적으로 결합하는 맞춤형 SLM[17]이 사용된다. DPAC은 이를 더 간단하게 통합하는 방식으로 식 (1)로 계산된 인접한 두 위상값을 바둑판 패턴으로 배치한다. 이 과정에서 sub-sampling으로 인한 정보 손실이 발생한다. 그림1의 예시와 같이 DPAC으로 생성된 위상 전용 홀로그램이 체크보드 패턴을 보이는 것을 확인할 수 있다.
2. 표준 압축 기술
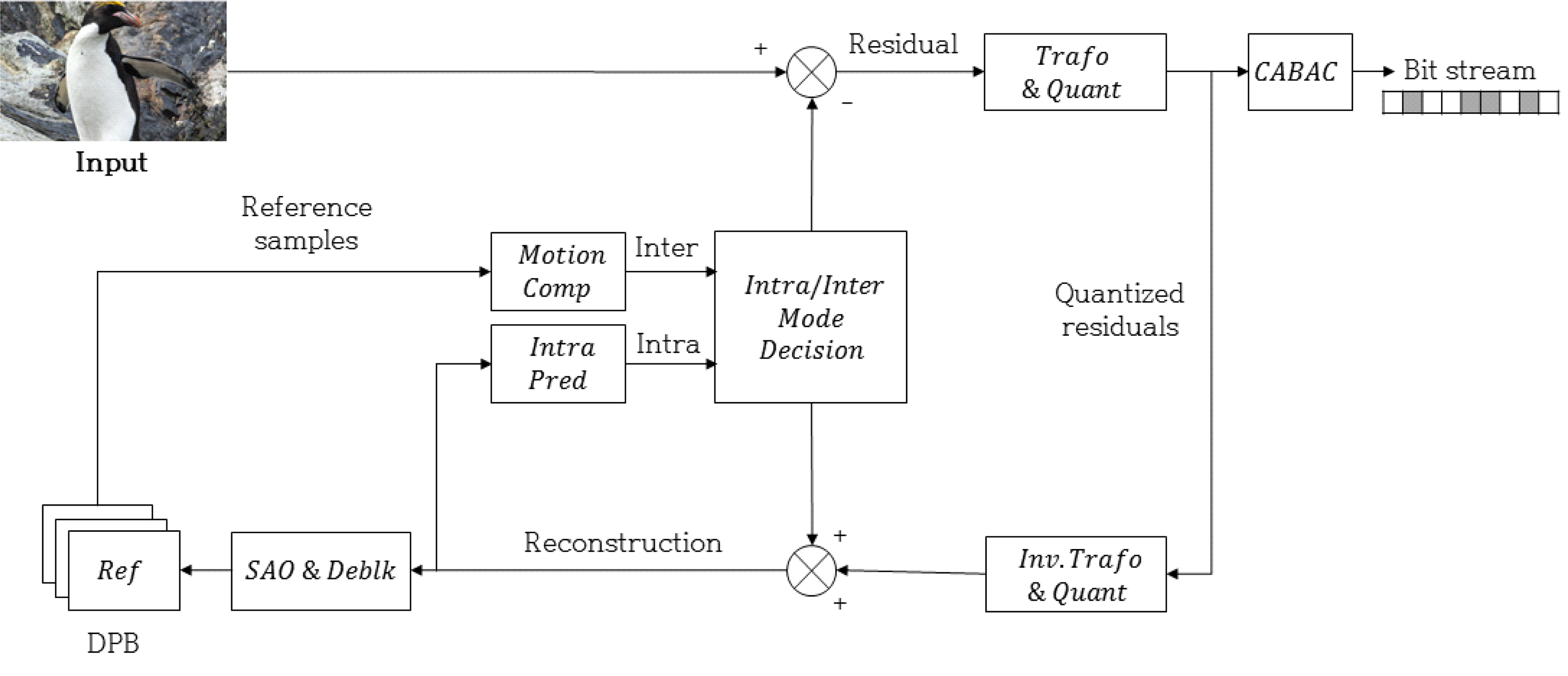
HEVC (High Efficiency Video Coding)는 고해상도 및 초고속 프레임율을 갖는 초고화질 디지털 비디오에 대한 수요가 증가함에 따라 ITU-T의 VCEG와 ISO/IEC MPEG에서 JCT-VC (Joint Collaborative Team on Video Coding)를 결성하며 개발되었다. HEVC는 이전 표준이었던 H.264/AVC과 전체적인 부호화 및 복호화 형태는 비슷하게 유지하면서 더욱 높은 고화질, 해상도의 비디오 압축 성능과 고속 병렬처리를 주요 목표로 하여 표준화되었다.
HEVC는 블록 단위의 하이브리드 영상 압축 기술로 입력 이미지 프레임 또는 슬라이스가 최대 크기 64×64의 여러 기본 처리 단위인 코딩 트리 단위(CTU)로 분할되어 처리된다. 래스터 스캔의 순서로 처리되는 각 블록은 공간적 또는 시간적 중복성을 제거하기 위해 공간적 또는 시간적 예측이 수행된다. 예측 후의 잔차 신호는 에너지 압축 계수를 얻기 위한 변환 모듈에 이어 양자화 모듈로 처리된다. 양자화 모듈은 양자화 매개변수(QP)에 의해 압축 강도가 결정되며 변환된 계수를 양자화하여 손실 코딩을 수행한다. 마지막으로 CABAC (Context-Adaptive Binary arithmetic coding)을 수행하여 통계적 중복성을 제거해 비트스트림으로 전송한다. 또한, 2개의 인루프 필터를 순차적으로 수행하여 코딩 효율성과 시각적 품질을 모두 높일 수 있다. 인루프 필터는 블로킹 아티팩트을 완화하기 위한 DBF (Deblocking Filter)와 재구성 샘플 간의 픽셀 오류를 줄이기 위한 SAO (Sample Adaptive Offset)로 구성되어 있다. HEVC 부호화기는 그림 2와 같다[18].
VVC (Versatile Video Coding)는 HEVC 이후의 최신 표준화 기술로 이전 세대의 코덱인 HEVC보다 2배 이상의 효율을 목표로 개발되었다. VVC에 포함된 기술들은 부호화 효율 향상과 복잡도 감소를 위해 HEVC의 영상분할구조, 화면 내 예측, 화면 간 예측, 변환, 양자화, 인 루프필터 및 엔트로피 코딩 각각의 단계에서 여러 모드 및 기술들이 변경되고 추가되었다[19].
3. 신경망 기반의 이미지 압축 기술
최근 몇 년간 신경망이 크게 주목받음에 따라 신경망 기반의 이미지 및 비디오 압축 모델이 활발히 연구되고 있다. 신경망 기반의 이미지 압축모델은 일반적으로 그림 3과 같이 Auto-encoder 구조로 인코더 분석기, 양자화 모듈, 엔트로피 인코더, 엔트로피 디코더, 디코더 합성기를 가진다. 초기 CNN 기반의 end-to-end 이미지 압축모델은 [20]에서 제안되었다. [20]의 모델을 발전시킨 구조로 [21]에서는 잠재 확률 분포의 매개변수를 예측하기 위한 부가정보로 hyperprior를 도입하였으며, [22]에서는 공간적 중복성을 활용하여 autoregressive 기반의 모듈을 도입한 모델로 확장했다. [23]은 인코더 및 디코더에 Attention module을 도입하고, 잠재 벡터 추정을 위해 가우시안 혼합 모델을 사용했다. 최근에는 [24]와 같이 전역적인 정보를 활용하여 CNN 구조의 단점을 보완할 수 있는 트랜스포머 기반의 압축모델들도 활발히 연구되고 있다.
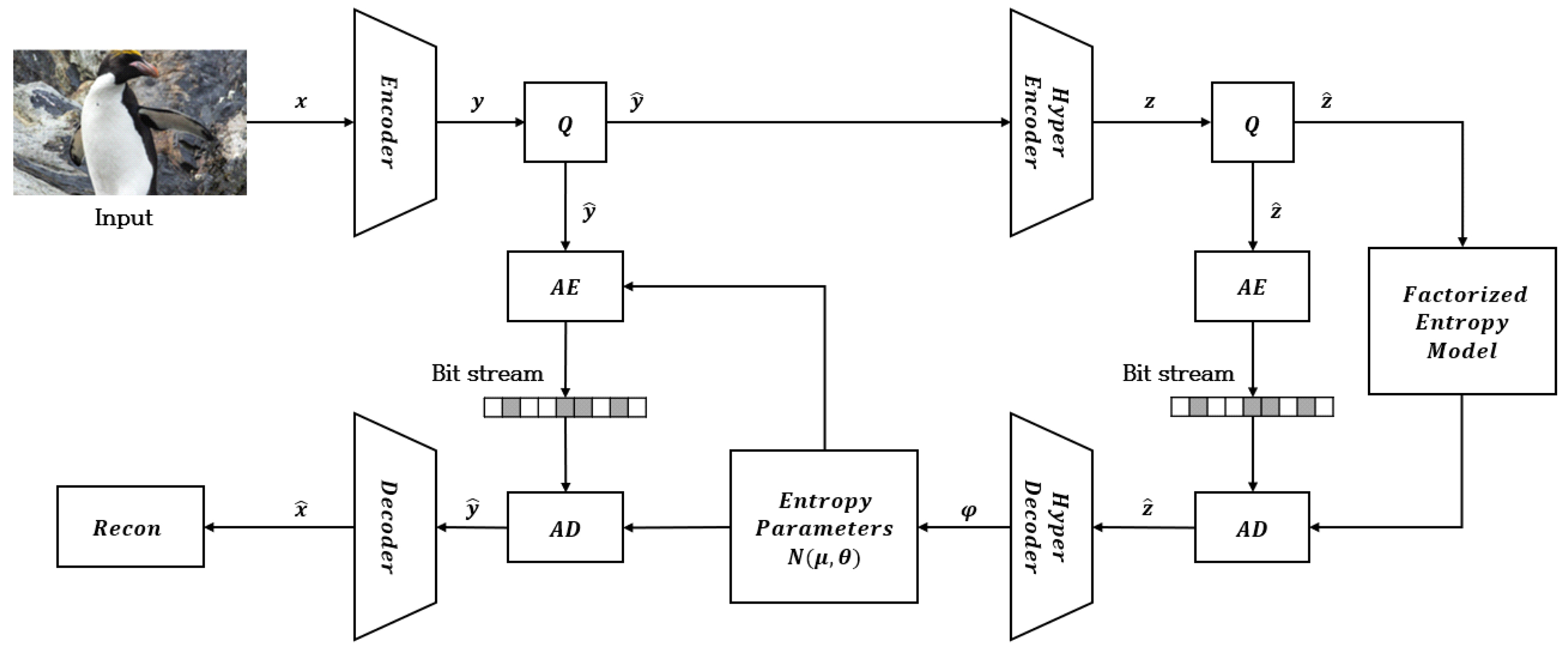
신경망 기반 부호화기 블록도Fig. 3. Block diagram of neural network based encoder, Q : Quantization, AE : Arithmetic Encoder, AD : Arithmetic Decoder
신경망 기반의 이미지 압축모델은 대부분 전체 이미지 단위로 처리된다. 이는 높은 계산 복잡도와 메모리 이슈를 가지며, 표준 코덱과의 호환성을 제공하기 어렵다. 블록 단위의 압축모델을 사용하면 이미지를 더 작은 블록 단위로 분할하여 처리하기 때문에 메모리 요구 사항을 줄일 수 있으며, 통상의 표준 코덱과도 호환될 수 있다[25]. 또한, 이전에 디코딩된 블록을 현재 블록 압축, 복원에 추가적인 정보로 활용할 수 있기 때문에 효율적인 코딩이 가능하다. [25]에서는 엔트로피 코딩을 위한 매개변수 예측에 디코딩된 주변 블록을 활용하여 좋은 성능을 보였다. [26]은 주변 블록을 인코딩 과정에 활용하고, 루마 신호를 크로마 신호 인코딩에 활용하면서 압축 효율을 높였다. [27]에서는 디코딩된 주변 블록 정보를 활용하여 공간적 예측을 수행하고 예측과의 잔차를 코딩하는 LBHIC (Learned Block-based Hybrid Image Compression) 모델을 제안하였다. 일반적으로 블록 단위 신경망 압축모델은 이미지 단위 모델보다 낮은 성능을 보이는 것에 반에 LBHIC은 이미지 단위 압축 모델과 비교해서도 좋은 성능을 달성했다. 본 논문에서는 신경망 기반의 블록 단위 압축에서 좋은 성능을 보인 LBHIC 모델을 POH 압축에 사용하였다.
4. 성능척도
POH의 압축 성능평가는 위상 홀로그램 도메인과 수치적 재구성(NR) 도메인 모두에서 수행된다. 홀로그램 도메인은 압축이 적용되는 위상 신호의 영역을 의미하며, NR 도메인은 수치적으로 재구성된 객체가 영상으로 표시되는 영역을 의미한다. 각 도메인에서의 성능평가는 표준 코덱 개발 시 코딩 효율을 정량화하기 위해 통상적으로 사용되는 Rate Distortion performance (RD-curve)와 Bjontegaard delta rate (BD-rate)[28]를 사용한다. 이때 화질평가는 객관적인 품질 메트릭인 PSNR (Peak Signal-to-Noise Ratio)을 사용한다. 위상 도메인에서의 PSNR 계산은 위상 주기성을 고려하기 위해 [29]에서 제안된 방식을 사용한다. 비트 전송률은 BPP (bits per pixel)로 측정되며 수식 (2)와 같이 계산할 수 있다.
Ⅲ. 제안 방법
위상 신호는 무작위적인 특성이 매우 강해 자연 영상과는 그 특성이 매우 다르다. 따라서 자연 영상에 대해 최적화된 통상의 압축 표준에서는 위상 신호를 효율적으로 압축하기 어렵다. 가장 최신 표준인 VVC는 자연 영상에서 좋은 압축 성능을 보이지만 위상 신호 압축은 잘되지 않는다.
최근 위상 신호 압축을 위한 툴로 학습 가능한 신경망 기반의 방법론이 연구되고 있다. 통상의 표준 압축 코덱은 다양한 입력 영상에 대해 적응적으로 최적화되기 어렵고, 개별 모듈을 공동으로 최적화하기 어렵다는 단점이 있지만, 신경망 기반의 방법론은 입력 영상에 대한 적응적 최적화가 가능하여 위상 신호 압축에 대해 좋은 성능을 기대할 수 있다. [12]는 POH의 생성 및 압축을 위한 end-to-end 기반의 신경망 모델을 제안하여 높은 압축 성능을 달성했다. 그러나 이는 이미지 단위의 신경망 모델로 높은 해상도의 홀로그램을 학습하기에는 큰 메모리가 요구된다.
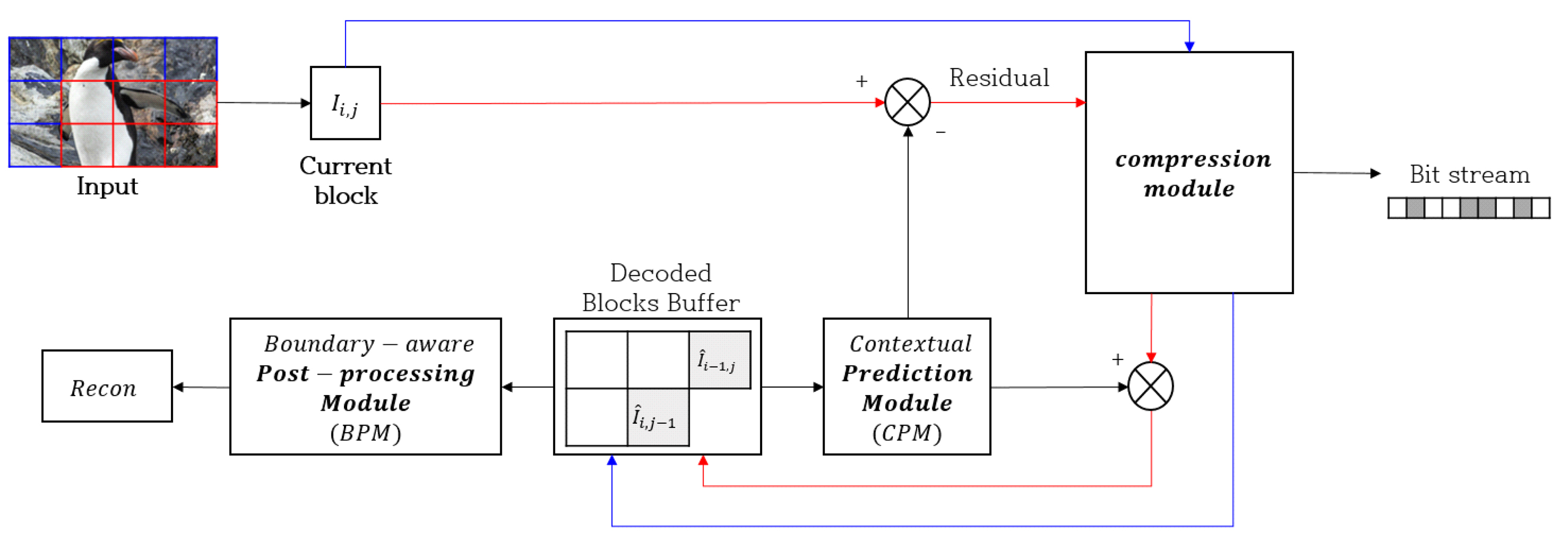
본 논문에서는 위상 신호에 대해 학습이 가능한 신경망 기반의 블록 단위 압축 모델을 사용하면 메모리 이슈를 해결하면서도 기존의 표준 압축 기술보다 높은 성능을 달성할 수 있음을 보였다. 실험에 사용된 신경망 모델 구조는 자연 영상에 대해 좋은 성능을 보인 LBHIC[27]을 기반으로 한다. LBHIC은 주변 블록을 활용하여 부호화하려는 대상 블록을 예측하는 예측 모듈(CPM), 대상 블록을 압축 복원하는 압축 모듈(Compression Module), 복원 화질을 높이기 위한 후처리 모듈(BPM)로 구성되어 있다. 입력 이미지는 블록 단위의 패치로 분할되어 순차적으로 예측, 압축, 후처리 모듈에 처리된다. 예측 모듈은 부호화할 대상 블록의 참조 블록이 디코딩되어 있다면 참조 블록을 입력으로 하여 예측 블록을 생성한다. 참조 블록은 부호화하고자 하는 블록(Ii,j)의 왼쪽
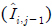 , 위
, 위
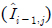 블록을 의미한다. 압축 모듈은 CNN 기반의 Auto-encoder 구조로 현재 블록과 예측 모듈에서 예측된 예측 블록과의 차분을 압축한다. 만일, 참조 블록이 없거나 부호화되지 않았다면 대상 블록을 압축한다. 압축 모듈에 입력된 블록은 비선형 레이어로 구성된 인코더에서 잠재 공간으로 변환되고, 변환된 잠재 벡터는 양자화된 후, 학습 가능한 엔트로피 모델과 산술 코딩을 걸쳐 비트스트림으로 압축된다. 이때 엔트로피 모델에서의 잠재 벡터 분포 추정을 위한 hyperprior 정보도 인코딩된다. hyperprior 인코더에서는 확률 모델의 파라미터를 추정하며, 잠재 벡터 분포의 매개변수화에는 정교한 추정을 위해 가우시안 혼합 모델이 사용된다. 추가적으로 autoregressive한 context model을 사용하여 엔트로피 파라미터 예측에 도움을 준다. 압축된 비트스트림은 압축 모듈 내의 디코딩 네트워크들을 걸쳐 복원 신호로 디코딩될 수 있다. 전체 블록에 대해 부호화 및 복호화가 완료되면 블로킹 아티팩트를 제거하기 위한 후처리 모듈이 수행된다. LBHIC의 전체적인 모델 구조는 그림 4와 같다.
블록을 의미한다. 압축 모듈은 CNN 기반의 Auto-encoder 구조로 현재 블록과 예측 모듈에서 예측된 예측 블록과의 차분을 압축한다. 만일, 참조 블록이 없거나 부호화되지 않았다면 대상 블록을 압축한다. 압축 모듈에 입력된 블록은 비선형 레이어로 구성된 인코더에서 잠재 공간으로 변환되고, 변환된 잠재 벡터는 양자화된 후, 학습 가능한 엔트로피 모델과 산술 코딩을 걸쳐 비트스트림으로 압축된다. 이때 엔트로피 모델에서의 잠재 벡터 분포 추정을 위한 hyperprior 정보도 인코딩된다. hyperprior 인코더에서는 확률 모델의 파라미터를 추정하며, 잠재 벡터 분포의 매개변수화에는 정교한 추정을 위해 가우시안 혼합 모델이 사용된다. 추가적으로 autoregressive한 context model을 사용하여 엔트로피 파라미터 예측에 도움을 준다. 압축된 비트스트림은 압축 모듈 내의 디코딩 네트워크들을 걸쳐 복원 신호로 디코딩될 수 있다. 전체 블록에 대해 부호화 및 복호화가 완료되면 블로킹 아티팩트를 제거하기 위한 후처리 모듈이 수행된다. LBHIC의 전체적인 모델 구조는 그림 4와 같다.
본 논문에서는 POH 압축에 대해 동일한 블록 기반의 압축 조건에서 학습 가능한 신경망 압축 기술이 자연 영상에 최적화된 기존의 표준 압축 코덱보다 좋은 성능을 달성할 수 있을지에 대한 가능성을 검증하기 위한 목적으로 단순화된 LBHIC 구조를 사용했다. 실제 사용된 네트워크는 후처리 모듈을 제외하고, 예측 모듈과 압축 모듈로만 구성되었다. 또한, 잠재 벡터의 분포 예측에는 싱글 가우시안 모델을 사용했다. 후처리 모듈을 통해 블로킹 아티팩트를 제거한다면 더 좋은 성능을 달성하겠지만, 본 논문에서는 가능성 검증 단계로써 블로킹 아티팩트가 존재하는 상황에서도 좋은 성능을 보일 수 있을지 확인하였다. 결과적으로 단순화된 신경망 구조로도 제안 방법이 매우 좋은 성능을 달성한 것을 확인할 수 있었다.
단순화된 신경망은 2.2절의 방식으로 생성한 POH 데이터셋에 대해 최적화되었으며, 학습은 총 세 개의 단계로 진행하였다. 첫 번째 단계에서는 각 블록에 대한 압축 성능을 높이기 위해 예측 모듈이 제외된 압축 모듈만을 학습했다. 두 번째 단계에서는 복원된 주변 블록으로부터 예측을 잘할 수 있도록 예측 모듈만을 학습했다. 세 번째 단계에서는 예측 및 차분 인코딩과 블록 인코딩을 동시에 잘할 수 있도록 전체 네트워크를 학습했다. 위상 신호는 자연 영상과 달리 채널 간 상관관계가 거의 없으므로 모든 학습 과정과 테스트 과정은 채널별로 진행하였다.
전체 학습 과정에서 신경망을 최적화하기 위한 손실함수 L은 수식 (3)에 나타낸 바와 같이 비트율 지표 R과 왜곡지표 D가 가중합하여 사용한다. 이때 비트율 R은 잠재 벡터의 엔트로피로 계산되며, 왜곡 D는 원본 영상(x)과 복원 영상(
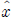 ) 간의 MSE를 이용하여 계산한다. λ는 비트율과 화질(복원 오차) 사이의 중요도에 따라 그 비율을 결정해주는 상수로, λ값이 증가할수록 복원 왜곡이 줄어들지만 비트율이 증가하게 된다[30].
) 간의 MSE를 이용하여 계산한다. λ는 비트율과 화질(복원 오차) 사이의 중요도에 따라 그 비율을 결정해주는 상수로, λ값이 증가할수록 복원 왜곡이 줄어들지만 비트율이 증가하게 된다[30].
Ⅳ. 실험결과
1. 실험 조건
실험을 위한 이미지 데이터셋으로는 DIV2K[31]를 사용했다. 홀로그램을 SLM에 변조하기 위해서는 물리적인 기술의 어려움으로 통상 2K 이상의 해상도가 요구되며, 실제 SLM 환경에서는 의미 있는 영역에 대한 관찰이 중요하기 때문에 최대한 SLM에서의 환경과 유사할 수 있도록 [15]와 같이 모든 이미지 데이터셋을 1600×880의 픽셀 영역을 갖도록 crop하고 1920×1080의 해상도를 갖도록 0으로 패딩하여 사용하였다. 의미 있는 영역에 대한 평가가 중요하므로 성능평가 시 원본 영상과 복원 영상의 왜곡은 픽셀 영역에서만 계산되었다. 신경망 학습에는 800개의 DIV2K train 데이터셋을 DPAC, GS, SGD의 방식으로 생성한 총 2400개의 POH를 사용하였고, 성능평가에는 100개의 DIV2K valid 데이터셋을 DPAC 방식으로 생성한 POH를 사용하였다. 이미지 데이터셋을 홀로그램으로 생성 시 [15]에서와 같은 조건으로 wavelength는 638, 520, 450nm, propagation distance는 20cm, pixel pitch는 6.4μm을 사용하였다. 이때, 이미지 데이터셋과 생성된 POH 데이터셋은 모두 각 색상 채널별로 8bit로 표현된다.
성능평가를 위한 기존의 표준 소프트웨어로는 HEVC reference software인 HM16.20[32]와 VVC reference software인 VTM11.0[33]을 사용하였다. HEVC의 QP는 22, 27, 32, 27, VVC의 QP는 17, 27, 32, 37을 사용하였으며, RGB 4:4:4 환경에서 압축을 진행했다. 신경망 모델의 학습 과정에서 수식 (3)의 λ는 128, 2048, 8192, 32768을 사용하였으며, 코딩 블록 단위는 128x128을 사용하였다. 신경망에 대한 테스트는 각각의 λ와 색상 채널별로 학습된 모델을 사용하였다. 실험에 사용된 모든 QP 및 λ는 각 코덱의 비트율-왜곡 그래프의 bpp range가 최대한 겹칠 수 있도록 설정하였다.
2. 표준 압축 코덱과의 비교
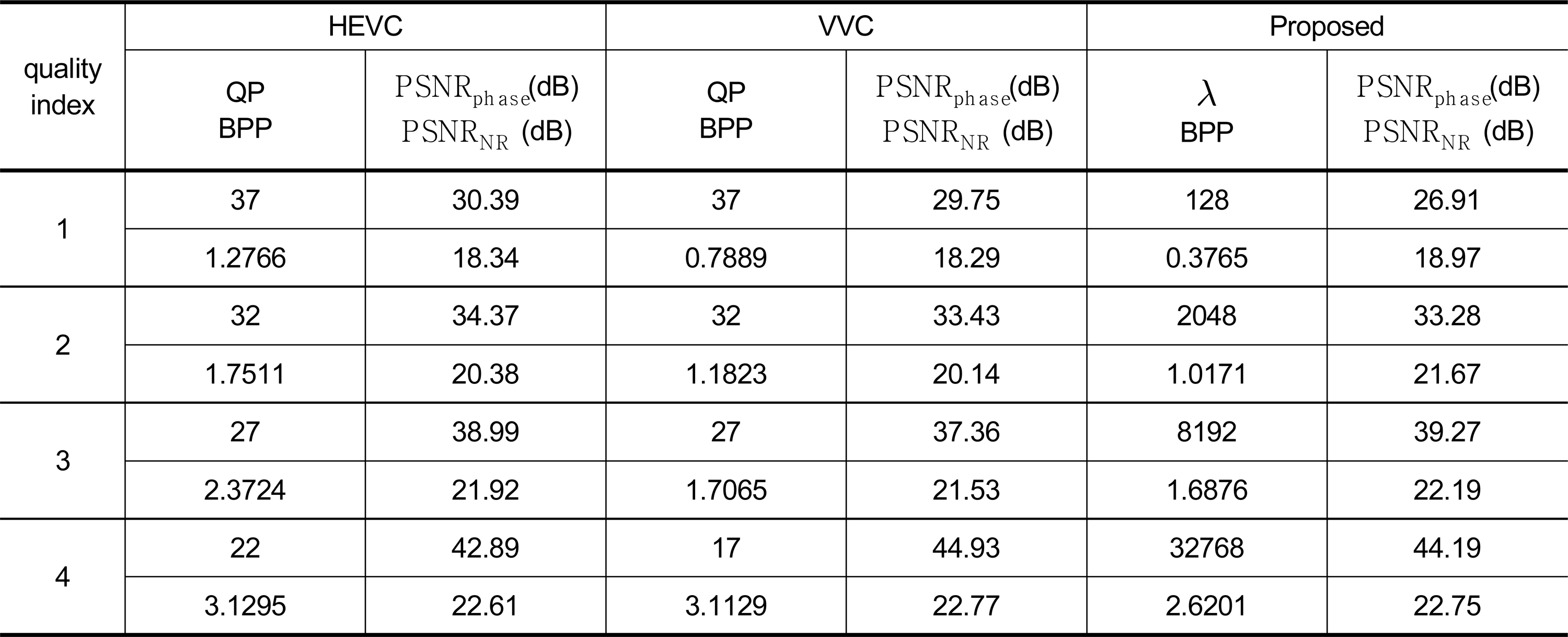
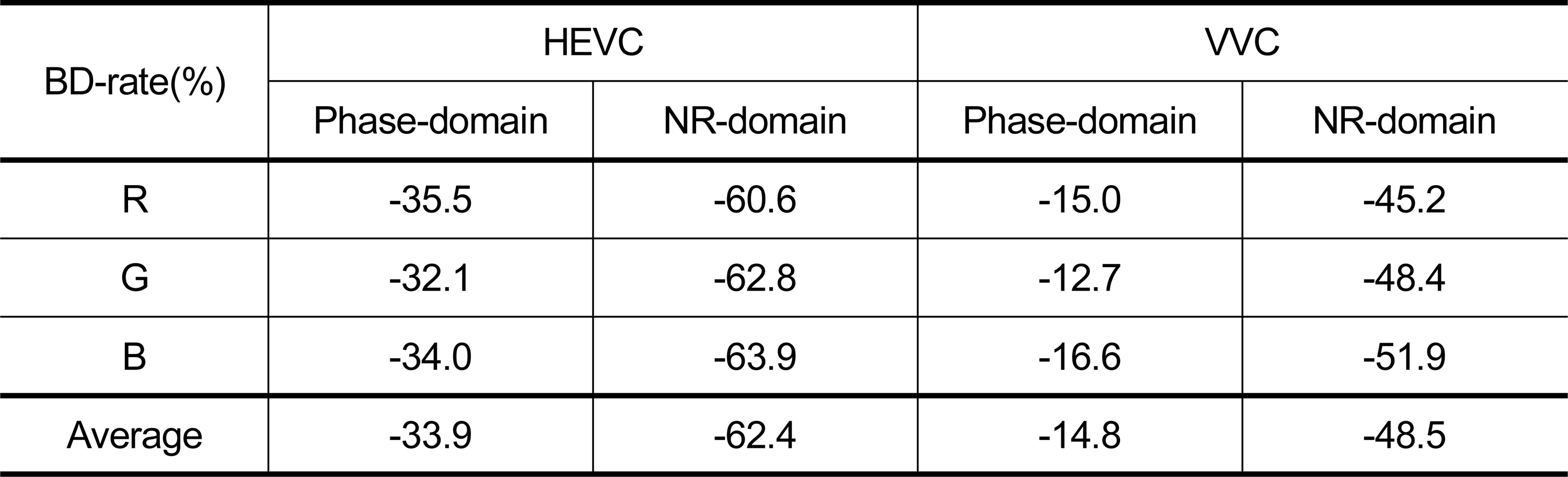
그림 5는 위상 도메인, 그림 6는 NR 도메인에서의 비트율-왜곡 성능을 보여준다. PSNR과 BPP는 100개의 모든 테스트 데이터셋 평균을 나타낸다. 그림 6의 DPAC 그래프는 무압축 상황에서 DPAC으로 생성한 POH의 수치적 복원 화질 평균으로 ground truth를 의미한다. 표 1은 여러 quality index에서 압축 복원된 각 기술의 성능을 보여준다. 실험 결과, 제안 방식은 블록 단위 인코딩이라는 동일 조건에서 HEVC와 VVC 대비 월등한 성능을 보여줬다. 표 2에서 볼 수 있듯이 제안 방식은 위상 도메인에서 HEVC 대비 –33.9%, VVC 대비 –14.8%의 평균 BD-rate 개선을 제공하였으며, NR 도메인에서 HEVC 대비 –62.4%, VVC 대비 –48.5%의 평균 BD-rate 개선을 달성하면서 월등히 좋은 성능을 보였다. 또한, 모든 채널에서 일관적으로 좋은 BD-rate를 보였음을 확인할 수 있다.
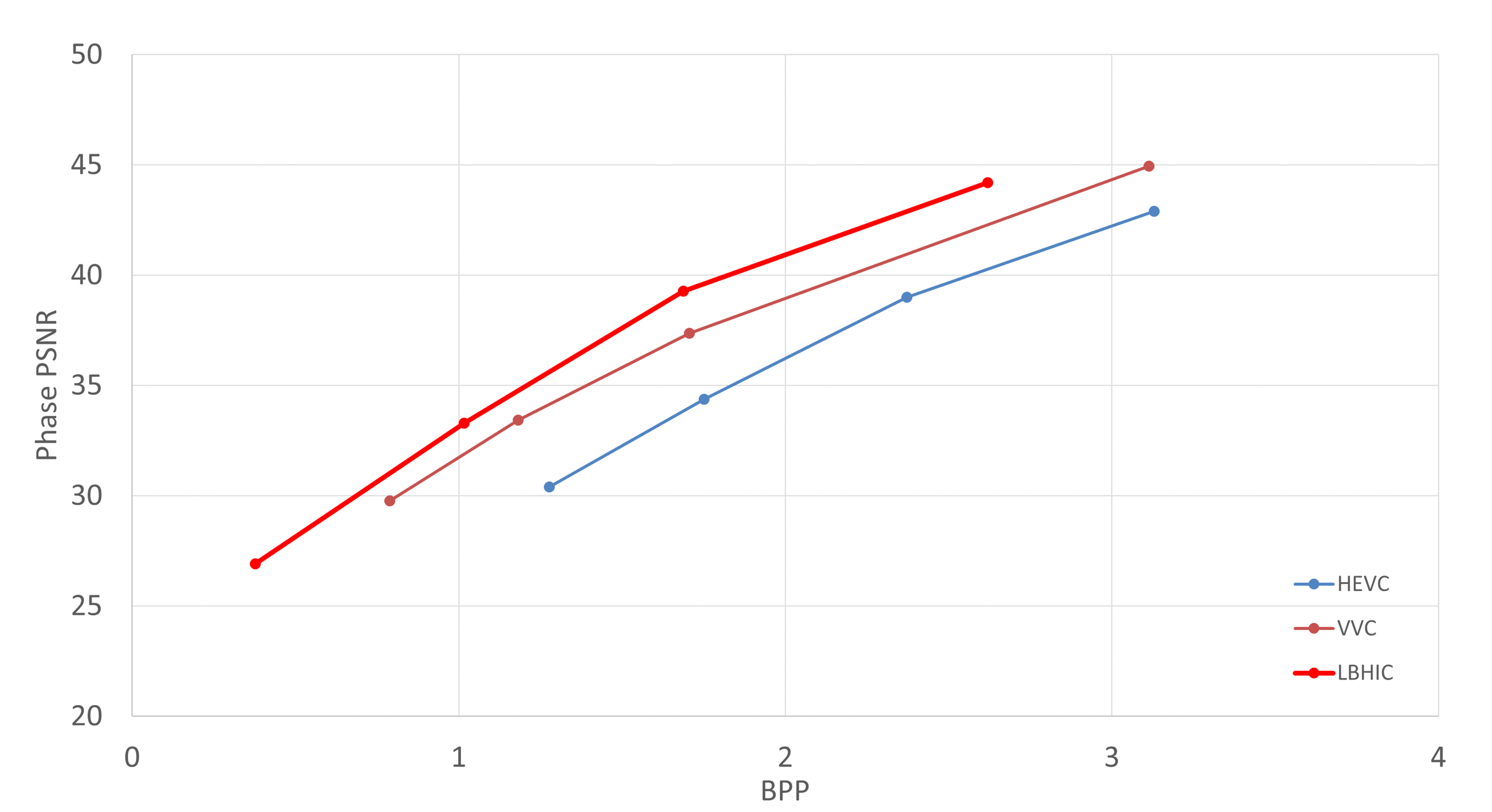
위상 도메인에서의 HEVC/VVC와 제안 방식의 비트율-왜곡 성능Fig. 5. Phase-domain RD performance of the HEVC/VVC and the proposed methods
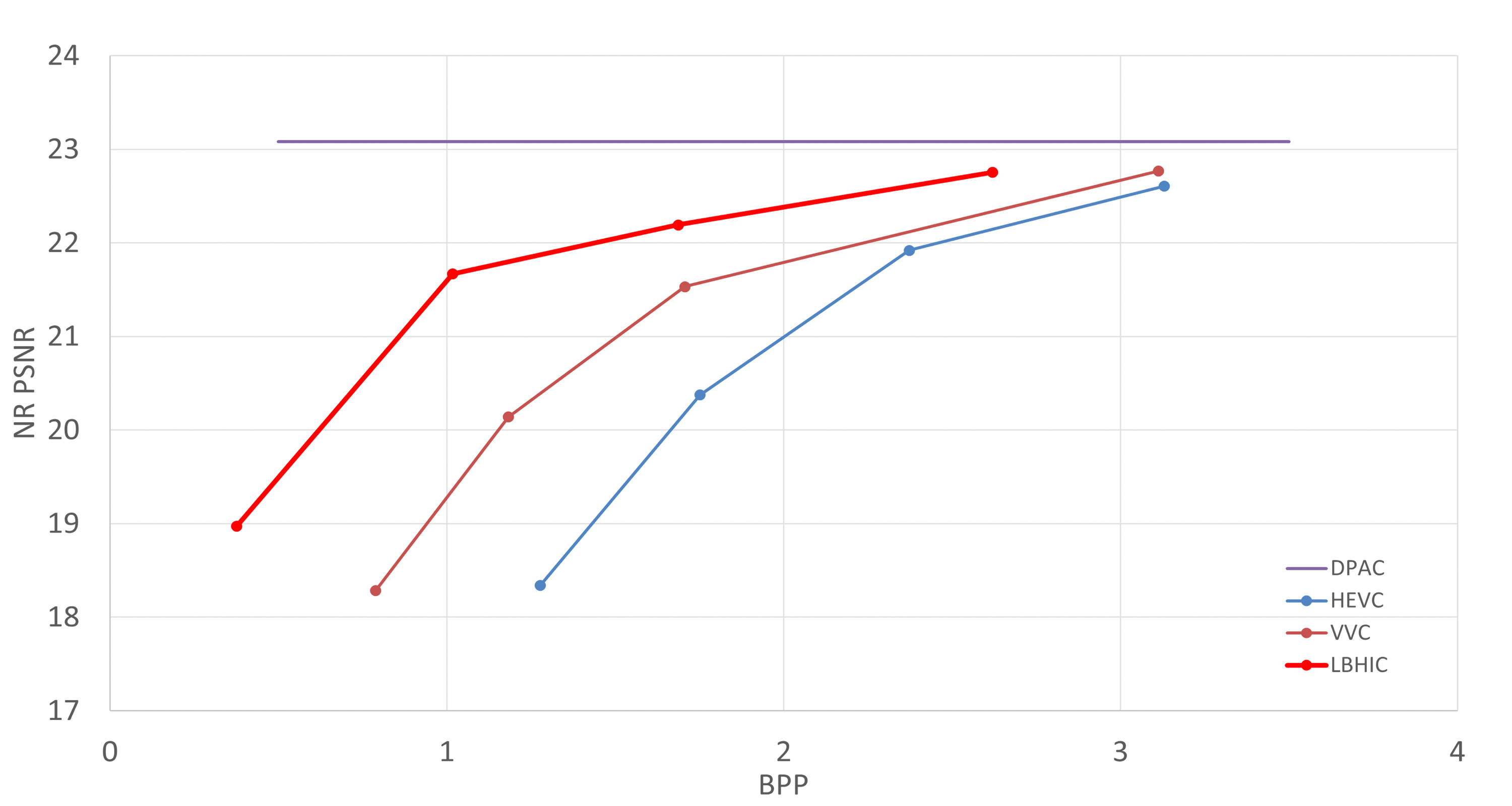
NR 도메인에서의 HEVC/VVC와 제안 방식의 비트율-왜곡 성능Fig. 6. NR-domain RD performance of the HEVC/VVC and the proposed methods
그림 7은 유사한 비트율에서 압축 복원된 홀로그램의 수치적 복원 화질을 차이를 보여준다. 비슷한 비트율 조건에서 압축 복원된 결과, 제안 방식이 기존 기술 대비 객관적 화질(PSNR)과 주관적 화질 모두 개선되었음을 알 수 있다. 제안 방식이 HEVC 및 VVC 대비 물체 영역에서 텍스쳐가 더 잘 표현되었으며, 배경 영역에서의 화질도 우수한 것을 확인하였다. 특히, HEVC와 제안 방식의 국소적인 화질을 비교해보면 전반적으로 컬러 노이즈가 줄어든 모습을 확인할 수 있다. 그림 8은 유사한 수치적 복원 화질을 가지는 조건에서 압축에 사용된 비트율 차이를 보여준다. 제안 방식은 기존 기술 대비 월등히 적은 비트량으로도 비슷한 화질을 달성했다. 반면, 유사한 PSNR에서 HEVC 대비 VVC를 비교한 결과, 비트율 측면에서 약 0.01~0.02 정도의 차이로 큰 성능 향상은 없었다. 실험 결과에 따라 POH 데이터에 대해서는 통상적인 표준 코덱보다 제안 방식과 같은 학습 가능한 신경망 기반의 압축 방식이 더 높은 압축 성능을 보일 수 있음을 알 수 있다.
3. 복소 홀로그램 코덱과의 비교
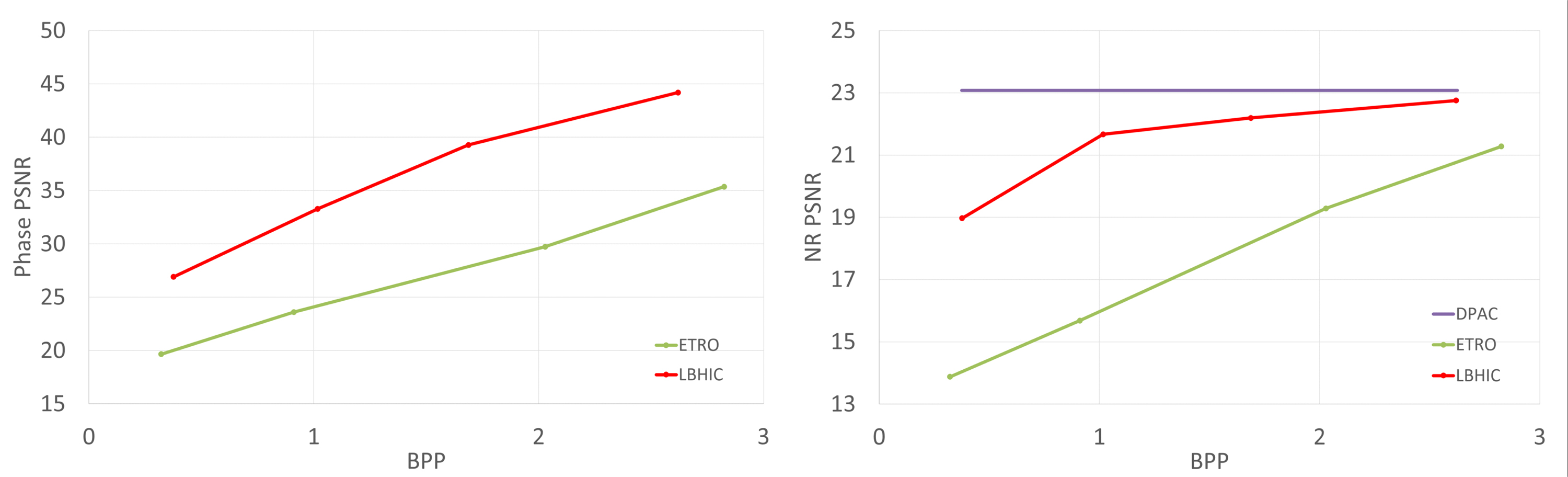
본 절에서는 ETRO에서 제안한 복소 홀로그램 압축 코덱(Interfere codec)[8]과의 성능을 비교한다. Interfere 코덱은 JPEG에 기고된 복소 홀로그램 압축을 위한 블록 단위 코딩 기술로 실수와 허수로 표현된 복소 데이터를 입력으로 받는다. Interfere 코덱은 복소 홀로그램 압축에 대해 HEVC보다 높은 성능을 낸 것으로 보고되고 있으나, 위상 전용 홀로그램 압축에 대한 성능평가는 아직 이루어지지 않았다. 본래 논문의 모티베이션은 위상 전용 홀로그램에 대한 신경망 기반의 블록 단위 압축 성능을 자연 영상에 최적화된 표준 코덱과 비교하여 검증하는 것이지만, 복소 홀로그램 압축을 위한 Interfere 코덱과 비교해서도 좋은 성능을 달성했음을 추가로 보였다.
본 논문에서는 위상 전용 홀로그램 압축에 대한 Interfere 코덱의 성능평가를 위해 실수, 허수부에 동일한 위상 전용 홀로그램을 입력하여 사용하였다. 공정한 비교를 위해 최종 비트량과 복원 성능 계산은 각 성분별 비트량의 평균과 각 성분별 복원성능의 평균을 사용하였다. 또한, 제안 방식의 코딩 블록 단위와 동일한 설정을 유지하기 위해 Coded block size를 128×128로 설정하였다. 압축 복원 신호의 SNR에 해당하는 코덱의 distortion option은 14.59, 18.82, 25.95, 31을 사용했다. 그림 9는 Phase 도메인, NR 도메인 각각에서 Interfere 코덱과 제안 방식의 평균 비트율-왜곡 성능을 보여준다. 실험 결과, 제안 방식이 Phase 도메인, NR 도메인에서 각각 Interfere 코덱 대비 BD-rate –78.8%, -66.3%로 모두에서 좋은 성능을 보인 것을 확인할 수 있다.
Ⅴ. 결론 및 향후 연구 방향
본 논문에서는 신경망 기반의 압축모델을 이용하면 블록 기반이라는 동일 조건 내에서도 표준 코덱보다 월등히 좋은 성능을 낼 수 있다는 것을 확인했다. 신경망 기반의 블록 단위 압축은 자연 영상을 위해 설계된 신경망 구조를 그대로 사용했음에도 불구하고 위상 전용 홀로그램에 대해 최적화한 것만으로 좋은 성능을 달성할 수 있었다. 기존 표준 코덱은 자연 영상에 최적화되어 있기 때문에 위상 홀로그램에서는 학습 가능한 신경망 기반의 압축이 더 유리한 것으로 분석된다. 추후의 연구에서 신경망 구조를 위상 신호에 적합한 구조로 설계한다면 더 좋은 성능을 얻을 수 있을 것으로 기대된다.
한편, 본 논문은 연구 결과의 한계도 존재한다. 본 논문에서는 수치적 복원 결과를 기반으로 평가를 진행했다. 그러나 홀로그램은 SLM을 통한 광학 복원 결과의 시각적 평가가 중요하므로 향후에는 이러한 평가를 추가할 필요가 있다. 또한, 본 논문에서는 [9], [12]의 기존 선행연구들과 같이 3D 홀로그램의 연구로 확장하기 전, 2D 홀로그램에 대해 먼저 아이디어를 적용하여 검증했다. 그러나 홀로그램은 3D 데이터이므로 다양한 깊이와 시야각을 고려한 압축 기술의 개발이 필요하며, 특히 다양한 깊이와 시야각 변화에 따라 입체감의 손실이나 chroma aberration 문제가 없는지 평가가 필요하다. 향후에는 본 논문의 방법을 기반으로 POH 압축의 성능을 개선하기 위한 연구를 진행할 예정이다.
Notes
References
-
Oh, K. J., Park, J., Research and Standardization Trends of Digital Hologram Compression, Electronics and telecommunications trends, (2019, Dec), 34(6), p145-155.
[https://doi.org/10.22648/ETRI.2019.J.340613]

-
Ko, Hyunsuk, Kim, Hui Yong, Deep learning-based compression for phase-only hologram, IEEE Access, (2021, May), 9, p79735-79751.
[https://doi.org/10.1109/ACCESS.2021.3084800]

-
Schelkens, Pete, et al , JPEG Pleno: Providing representation interoperability for holographic applications and devices, ETRI Journal, (2019, Feb), 41(1), p93-108.
[https://doi.org/10.4218/etrij.2018-0509]

-
Darakis, Emmanouil, Soraghan, John J., Compression of interference patterns with application to phase-shifting digital holography, Applied optics, (2006), 45(11), p2437-2443.
[https://doi.org/10.1364/AO.45.002437]

-
Blinder, David, et al. , JPEG 2000-based compression of fringe patterns for digital holographic microscopy, Optical Engineering, (2014, Dec), 53(12), p123102-123102.
[https://doi.org/10.1117/1.OE.53.12.123102]

-
Darakis, Emmanouil, et al. , Visually lossless compression of digital hologram sequences, Image Quality and System Performance VII, SPIE, (2010, Jan), 7529, p362-369.
[https://doi.org/10.1117/12.840234]

-
Xing, Yafei, Pesquet-Popescu, Béatrice, Dufaux, Frederic, Compression of computer generated phase-shifting hologram sequence using AVC and HEVC, Applications of Digital Image Processing XXXVI, SPIE, (2013, Sep), 8856, p531-538.
[https://doi.org/10.1117/12.2027148]

- JPEG (ISO/IEC JTC1/SC29/WG1), JPEG Pleno: Interfere codec V1.00 interface description, WG1M94003, (2021, November).
-
Jiao, Shuming, et al. , Compression of phase-only holograms with JPEG standard and deep learning, Applied Sciences, (2018, July), 8(8), p1258.
[https://doi.org/10.3390/app8081258]

-
Tu, Han-Yen, Hsieh, Ching-Huang, Hoang, Huong-Giang, Compression of phase image for three-dimensional object, 2014 21st International Workshop on Active-Matrix Flatpanel Displays and Devices (AM-FPD), IEEE, (2014, July), p97-100.
[https://doi.org/10.1109/AM-FPD.2014.6867135]

-
Shi, Liang, et al. , Towards real-time photorealistic 3D holography with deep neural networks, Nature, (2021, Mar), 591(7849), p234-239.
[https://doi.org/10.1038/s41586-021-03476-5]

-
Wang, Yujie, et al. , Joint Neural Phase Retrieval and Compression for Energy-and Computation-Efficient Holography on the Edge, Association for Computing Machinery, (2022, July), 41(4), p1-16.
[https://doi.org/10.1145/3528223.3530070]

-
Shechtman, Yoav, et al. , Phase retrieval with application to optical imaging: a contemporary overview, IEEE signal processing magazine, (2015, April), 32(3), p87-109.
[https://doi.org/10.1109/MSP.2014.2352673]

-
Maimone, Andrew, Georgiou, Andreas, Kollin, Joel S., Holographic near-eye displays for virtual and augmented reality, ACM Transactions on Graphics (Tog), (2017, Aug), 36(4), p1-16.
[https://doi.org/10.1145/3072959.3073624]

-
Peng, Yifan, et al. , Neural holography with camera-in-the-loop training, ACM Transactions on Graphics (TOG), (2020, Dec), 39(6), p1-14.
[https://doi.org/10.1145/3414685.3417802]

-
Hsueh, Chung-Kai, Sawchuk, Alexander A., Computer-generated double-phase holograms, Applied optics, (1978), 17(24), p3874-3883.
[https://doi.org/10.1364/AO.17.003874]

-
Reichelt, Stephan, Leister, Norbert, Computational hologram synthesis and representation on spatial light modulators for real-time 3D holographic imaging, Journal of Physics: Conference Series, IOP Publishing, (2013), 415(1), p012038.
[https://doi.org/10.1088/1742-6596/415/1/012038]

-
Sullivan, Gary J., et al , Overview of the high efficiency video coding (HEVC) standard, IEEE Transactions on circuits and systems for video technology, (2012, Dec), 22(12), p1649-1668.
[https://doi.org/10.1109/TCSVT.2012.2221191]

-
Bross, Benjamin, et al. , Overview of the versatile video coding (VVC) standard and its applications, IEEE Transactions on Circuits and Systems for Video Technology, (2021, Oct), 31(10), p3736-3764.
[https://doi.org/10.1109/TCSVT.2021.3101953]

-
Ballé, Johannes, Laparra, Valero, Simoncelli, Eero P., End-to-end optimized image compression, International Conference on Learning Representations, (2016, Nov).
[https://doi.org/10.48550/arXiv.1611.01704]

-
Ballé, Johannes, et al. , Variational image compression with a scale hyperprior, International Conference on Learning Representations, (2018).
[https://doi.org/10.48550/arXiv.1802.01436]

-
Minnen, David, Ballé, Johannes, Toderici, George D., Joint autoregressive and hierarchical priors for learned imagecompression, Advances in Neural Information Processing Systems, (2018), p10771-10780.
[https://doi.org/10.48550/arXiv.1809.02736]

-
Cheng, Zhengxue, et al. , Learned image compression with discretized gaussian mixture likelihoods and attention modules, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, (2020), p7939-7948.
[https://doi.org/10.48550/arXiv.2001.01568]

-
Zou, Renjie, Song, Chunfeng, Zhang, Zhaoxiang, The Devil Is in the Details: Window-based Attention for Image Compression, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, (2022, Mar), p17492-17501.
[https://doi.org/10.48550/arXiv.2203.08450]

-
Yuan, Zhongzheng, et al. , Block-based Learned Image Coding with-Convolutional Autoencoder and Intra-Prediction Aided Entropy Coding, 2021 Picture Coding Symposium (PCS), IEEE, (2021, June), p1-5.
[https://doi.org/10.1109/PCS50896.2021.9477503]

-
Brand, Fabian, Seiler, Jürgen, Kaup, Andre, Intra-frame coding using a conditional autoencoder, IEEE Journal of Selected Topics in Signal Processing, (2020, Feb), 15(2), p354-365.
[https://doi.org/10.1109/JSTSP.2020.3034768]

-
Wu, Yaojun, et al. , Learned block-based hybrid image compression, IEEE Transactions on Circuits and Systems for Video Technology, (2020, Dec), 32(6), p3978-3990.
[https://doi.org/10.48550/arXiv.2012.09550]

- Bjontegaard, G., Improvements of the BD-PSNR model, Doc. VCEG-AI11, ITU-T SG16/Q6 VCEG, 35th meeting, Berlin, (2008).
-
Oh, Kwan‐Jung, Kim, Jinwoong, Kim, Hui Yong, A New Objective Quality Metric for Phase Hologram Processing, ETRI Journal, (2022, Dec), 44(1), p94-104.
[https://doi.org/10.4218/etrij.2021-0209]

-
Kim, Yeongwoong, et al. , Latent Shifting and Compensation for Learned Video Compression, Journal of Broadcast Engineering, (2022, Jan), 27(1), p31-43.
[https://doi.org/10.5909/JBE.2022.27.1.31]

-
Agustsson, Eirikur, Timofte, Radu, Ntire 2017 challenge on single image super-resolution: Dataset and study, Proceedings of the IEEE conference on computer vision and pattern recognition workshops, (2017, Aug), p126-135.
[https://doi.org/10.1109/CVPRW.2017.150]

- Reference software of HEVC (HM), https://hevc.hhi.fraunhofer.de/svn/svn_HEVCSoftware/tags/HM-16.20/, accessed Dec, 31, 2020.
- Reference software of VVC (VTM), https://vcgit.hhi.fraunhofer.de/jvet/VVCSoftware_VTM/, accessed Oct, 12, 2021.
최 승 미
- 2022년 : 경희대학교 컴퓨터공학과 학사
- 2022년 ~ 현재 : 경희대학교 컴퓨터공학과 석사과정
- 주관심분야 : 영상처리, 비디오 부호화, 인공지능, 디지털 홀로그램
박 수 용
- 2017년 ~ 현재 : 경희대학교 전자공학과 학사
- 주관심분야 : 영상처리, 비디오 부호화, 인공지능
반 현 민
- 2021년 : 경희대학교 컴퓨터공학과 학사
- 2021년 ~ 현재 : 경희대학교 컴퓨터공학과 석사과정
- 주관심분야 : 영상처리, 비디오 부호화, 딥러닝, 디지털 홀로그램
차 준 영
- 2017년 3월 ~ 현재 : 경희대학교 소프트웨어융합학과 학사
- 주관심분야 : 영상처리, 비디오 부호화, 딥러닝, 디지털 홀로그램
김 휘 용
- 1994년 8월 : KAIST 전기및전자공학과 공학사
- 1998년 2월 : KAIST 전기및전자공학과 공학석사
- 2004년 2월 : KAIST 전기및전자공학과 공학박사
- 2003년 8월 ~ 2005년 10월 : ㈜애드팍테크놀러지 멀티미디어팀 팀장
- 2005년 11월 ~ 2019년 8월 : 한국전자통신연구원(ETRI) 실감AV연구그룹 그룹장
- 2013년 9월 ~ 2014년 8월 : Univ. of Southern California (USC) Visiting Scholar
- 2019년 9월 ~ 2020년 2월 : 숙명여자대학교 전자공학전공 부교수
- 2020년 3월 ~ 현재 : 경희대학교 컴퓨터공학과 부교수
- 주관심분야 : 비디오 부호화, 딥러닝 영상처리, 디지털 홀로그램