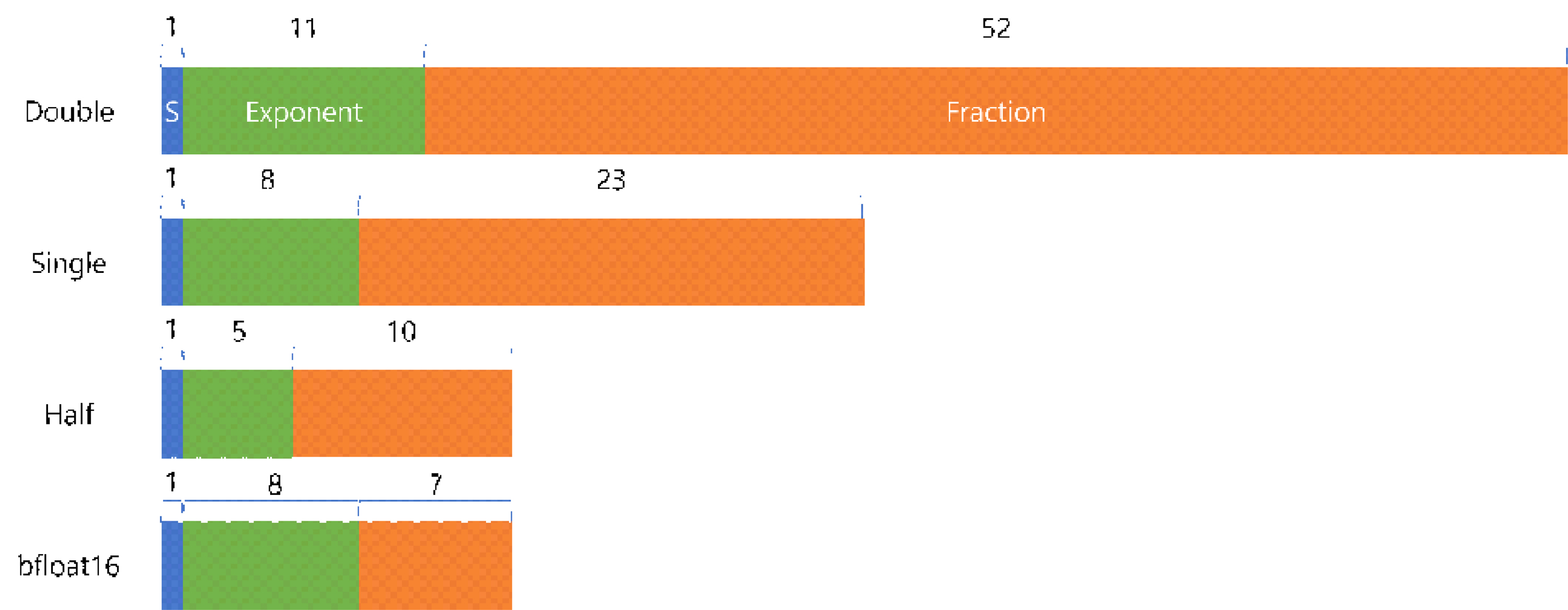회절연산 정밀도에 따른 CGH 기반 홀로그램 생성 품질 분석

Ⅰ. 서 론

홀로그래피(holography)는 빛의 파동을 홀로그램에 기록하는 기술로 빛의 세기(intensity)를 기록하는 사진(photography)과 다르게 기록한 장면의 3차원 정보를 재현할 수 있다는 장점을 가진다. 컴퓨터 생성 홀로그래피(computer generated holography, CGH)는 컴퓨터 연산을 통해 홀로그램을 생성하는 방법이다. CGH는 공간적, 시간적 제약을 넘어 가상 공간을 활용하여 홀로그램을 생성할 수 있다는 장점을 가진다. 하지만 홀로그램은 일반 이미지나 영상 대비 수~수십 배 높은 해상도를 요구하며 복소수 연산을 요구함에 따라, 연산 부하와 메모리 요구량이 크다. 이러한 연산적 공간적 요구 문제를 해결하기 위해, 다양한 CGH 가속 알고리즘들과 특화 하드웨어 장치들이 연구되고 있다^[1-4].

CGH는 빛의 회절(diffraction) 연산에 기반을 두며, 회절 연산은 복소수 행렬 연산과 푸리에 변환(Fourier transform)을 포함한다. 푸리에 변환은 주로 고속 푸리에 변환(fast Fourier transform, FFT)을 통해 수행된다. FFT는 이산 푸리에 변환(discrete Fourier transform, DFT)의 연산 복잡도를 낮춘 고속화 알고리즘으로, CGH 뿐만 아니라, 컴퓨터 비전, 파동 분석, 인공지능, 음향 기술 등 폭넓게 사용된다^[5,6]. FFT 연산 속도를 높이기 위해, 다중코어 CPU, SIMD (Single Instruction, Multiple Data), GPU(Graphics Processing Unit) 등과 같은 병렬처리 장치를 활용하는 기술들이 연구되어 왔다^[7-16]. 대표적인 병렬처리 기반 FFT 라이브러리에는 oneAPI^[17], cuFFT^[18], rocFFT^[19], 그리고 FFTW^[20,21] 등이 있다.

일반적인 연산장치(또는 산술연산코어)에서 연산 정밀도와 속도는 반비례한다. 따라서, 정확도를 일부 포기하며 연산 정밀도를 낮추면, 더 높은 연산 처리 성능을 기대할 수 있다. 정밀도를 낮춘다는 것은 또한 데이터의 크기도 작아진다는 것을 의미한다. 따라서, 데이터 접근시간이 감소하며, 한 번에 처리할 수 있는 데이터의 크기가 증가한다는 장점을 가진다. 최신 Nvidia사의 GPU들은 낮은 정밀도의 행렬 곱셈에 특화된 연산장치인 텐서 코어(tensor core)를 가지고 있으며, bfloat16(brain floating point)^[22,23]과 TF32(TensorFloat-32)등의 다양한 산술정밀도를 지원한다. 최근 인공지능, 빅데이터 연구 분야에서는 연산 정밀도(precision)를 낮추고 연산속도를 높이는 반정밀도(half precision, fp16) 연산과 혼합정밀도(mixed precision) 연산을 채용하고 있다^[23,24].

부동소수점(floating-point)에서 소수부에 대한 정확도는 사용하는 비트의 수에 따라 달라진다^[25]. 따라서 정밀도가 낮을수록 연산결과의 정확도가 낮아진다. 또한, 연산을 거듭해서 수행할수록 연산오류가 누적되어 오차가 커진다. 홀로그램 연산은 부동소수점을 이용한 복소수 연산을 반복한다. 그리고 수의 범위가 10-9-105 수준으로 넓기 때문에, 정밀도가 낮은 경우 홀로그램의 품질이 크게 저하될 수 있다. 아울러, 푸리에 변환은 행렬의 모든 원소에 인자를 곱하고 더하는 과정을 거치기 때문에, 행렬의 크기가 커질수록 연산횟수가 가파르게 증가하며, 정밀도 오차 더욱 커질 수 있다. 따라서, 적정 수준의 품질을 유지하면서 연산 속도를 높일 수 있는 정밀도에 대한 연구가 필요하다. 본 연구는 정밀도에 따라 생성된 홀로그램 결과를 비교 및 분석한다. 연구에 사용한 정밀도는 배정밀도(double-precision), 단정밀도(single-precision), 그리고 bfloat16를 포함하며, 각 스펙트럼 방법(angular spectrum method)을 회절에 연산에 사용하였다.

각각의 정밀도별 회절 연산을 비교분석한 결과 bfloat16이 배정밀도와 단정밀도 대비 최대 5.94배, 1.52배 빠른 연산 성능을 보여주었다. 또한, 해상도가 증가하면서 정밀도에 의한 오차가 홀로그램 정성적 품질에는 큰 영향을 끼치지 않음을 보여주었다. 이러한 결과는, 낮은 정밀도 연산을 CGH에 적용할 수 있는 가능성을 보여준다.

Ⅱ. 관련연구

CGH 생성방식은 3차원 장면의 샘플링 방법에 따라 포인트(point), 메시(mesh), 레이어(layer), 그리고 라이트필드(lightfield) 등으로 분류할 수 있다^[2]. 메시, 레이어, 라이트필드 등은 주로 푸리에 변환을 이용하며, 포인트 CGH는 WRP(Wavefront Recording Plane) 방법^[26]을 이용할 때 푸리에 변환을 사용한다. 최근 고성능 컴퓨팅 분야에서 방대한 데이터를 빠르게 처리하기 위해 정밀도를 낮추고 연산 속도와 메모리 이익을 얻는 방법이 연구되고 있다^{[23, 27-32]}. 이러한 저 정밀도 연산은 홀로그램에도 적용될 수 있다. David Blinder와 Peter Schelkens(2021)는 삼각함수를 8비트 정수로 연산하여 포인트 기반 홀로그램 생성 속도를 높이는 방법을 제안하였다^[33]. 8비트 연산을 이용하여 낮아진 정밀도를 보간하여 약 1.3배, 정밀도 보간 없이 최대 3.1배 빠른 홀로그램 생성 속도를 보인다.

텐서 코어는 합성곱 연산에 특화된 연산가속장치로 혼합 정밀도를 사용하여 기존 GPU코어 대비 2.5-12배 더 빠른 성능을 보인다^[34]. FFT는 연산과정에 행렬 곱셈을 이용하기 때문에 텐서 코어를 활용하는 것이 가능하다^[35-38]. A. Sorna 외(2018)는 텐서코어를 이용하여 FFT 연산을 가속화하고 낮은 정밀도에 의한 오차를 줄이는 방법을 제안하였다. 연산 속도가 cuFFT에 비해 낮은 문제가 있었지만, Binrui Li 외(2021), Sultan Durrani 외(2021), Louis Pisha와 Łukasz Ligowski(2021) 등의 연구에서 텐서코어를 활용하여 cuFFT에 비해 높은 연산속도를 갖는 FFT 연산 방법을 제안하였다^[35,37,38].

Ⅲ. 부동소수점과 정밀도

컴퓨터는 실수를 표현하기 위해서 부동소수점을 이용한다. 부동소수점은 IEEE754 표준에 따라서 배정밀도, 단정밀도, 반정밀도 등으로 분류된다^[25]. bfloat16는 최근 TPU(Tensor Processing Unit), GPU 등의 각종 전용 프로세서에서 지원하고 있는, 반정밀도의 단점을 완화하기 위한 정밀도이다. CPU는 일반적으로 단정밀도와 배정밀도를 동일한 부동소수점 처리장치에서 처리하기 때문에 연산속도 차이가 미미하다. 반면, GPU의 연산코어는 정밀도별 연산 속도가 다르다. 최근 GPU는 각 스트리밍 코어(streaming core)에 SIMD연산을 도입하여 반정밀도와 같은 낮은 정밀도 연산을 가속한다. 특히, Nvidia의 텐서 코어는 반정밀도와 단정밀도를 혼합한 혼합정밀도를 지원하며 반정밀도의 오차를 줄이면서도, 단정밀도보다 빠른 연산 성능을 보여준다^[34].

본 연구는 배정밀도, 단정밀도, 반정밀도, bfloat16를 활용한 홀로그램 생성 품질을 비교한다. 그림 1은 각 부동소수점의 정밀도 별 비트 크기와 구성을 보여준다. 부동소수점 방식은 실수를 부호비트(sign), 가수부(exponent), 소수부(fraction)의 조합으로 표현한다. 부호비트는 양수와 음수를 판단하는 비트이며 가수부는 숫자의 자릿수를 판단한다. 소수부는 표현하는 수의 소수점을 표현한다. 부호비트의 크기는 모든 정밀도가 1비트로 동일하며 가수부와 소수부는 정밀도에 따라 크기가 다르다. 부동소수점의 표현 방법은 수식 1과 같다.

그림 1.

부동소수점의 비트 구성Fig. 1. Structure of floating point numbers

n은 부동소수점으로 표현된 수, S는 부호비트, F는 소수부의 크기, E는 가수부의 바이어스(bias), e는 가수부의 값(0~2e), b_x는 x번째 비트 값이다. F가 클수록 소수점을 표현할 수 있으며 E가 클수록 더 넓은 범위의 수를 표현하는 것이 가능하다. 예를 들어, 배정밀도의 가수부는 11비트로 [2^-1023, 2¹⁰²⁴]의 자릿수를 표현할 수 있으며 소수부는 52비트로 1~(2^-252)의 수를 표현할 수 있다. 단정밀도의 가수부는 8비트로 [2^-126, 2¹²⁷]의 자릿수를 표현할 수 있으며 소수부는 23비트로 2²³개의 수를 표현할 수 있다. 반정밀도의 경우, 가수부의 길이가 5비트로 [2^-14, 2¹⁵]의 수를 표현할 수 있다.

부동소수점에서 e=0인 경우를 준 정규 값(subnormal number)이라 한다. 준 정규 값은 언더플로우(underflow)를 막기 위한 값으로 일반적인 부동소수점 표현방식에 차이가 있으며, 연산속도가 달라질 수 있다. 따라서, 본 논문에서는 준 정규 값을 배제하고 정규 값만을 비교 분석한다.

부동소수점이 표현할 수 있는 가장 작은 수는 수식 2, 가장 큰 수는 수식 3과 같다. 예를 들어, 반정밀도의 경우, F=10, E=15 이므로 표현가능한 가장 작은 수는 (1+2^-10) × 2^-14=6.10*10^-15이며, 가장 큰 수는 (2-2^-10) × 2¹⁵=65.504 이다. 표 1은 각 정밀도별 표현가능한 수를 보여준다.

표 1.

부동소수점 정밀도 표현 범위Table 1. Value range of floating point numbers

Ⅳ. 회절연산 구현

회절연산은 홀로그램 면에 도달하는 빛의 파동을 홀로그램 면에 기록하고 분석한다. 회절연산은 주로 각 스펙트럼 방법(angular spectrum method)과 프레넬 회절(Fresnel diffraction)을 이용한다. 본 논문의 실험에서는 각 스펙트럼 방법을 사용한다. 각 스펙트럼 방법은 수식 4와 같다. 수식 4의 연산절차와 본 연구에서 사용한 정밀도는 그림 2와 같다. 수식 4는 Forward FFT, Scaling, Multiply Transfer, Backward FFT 순으로 수행된다. 본 연구에서는 배정밀도(FP64), 단정밀도(FP32), bfloat16(BF16) 정밀도를 이용하며 Scaling과 Multiply Transfer 연산에는 BF16 대신 FP32를 이용하였다 (그림 2).

그림 2.

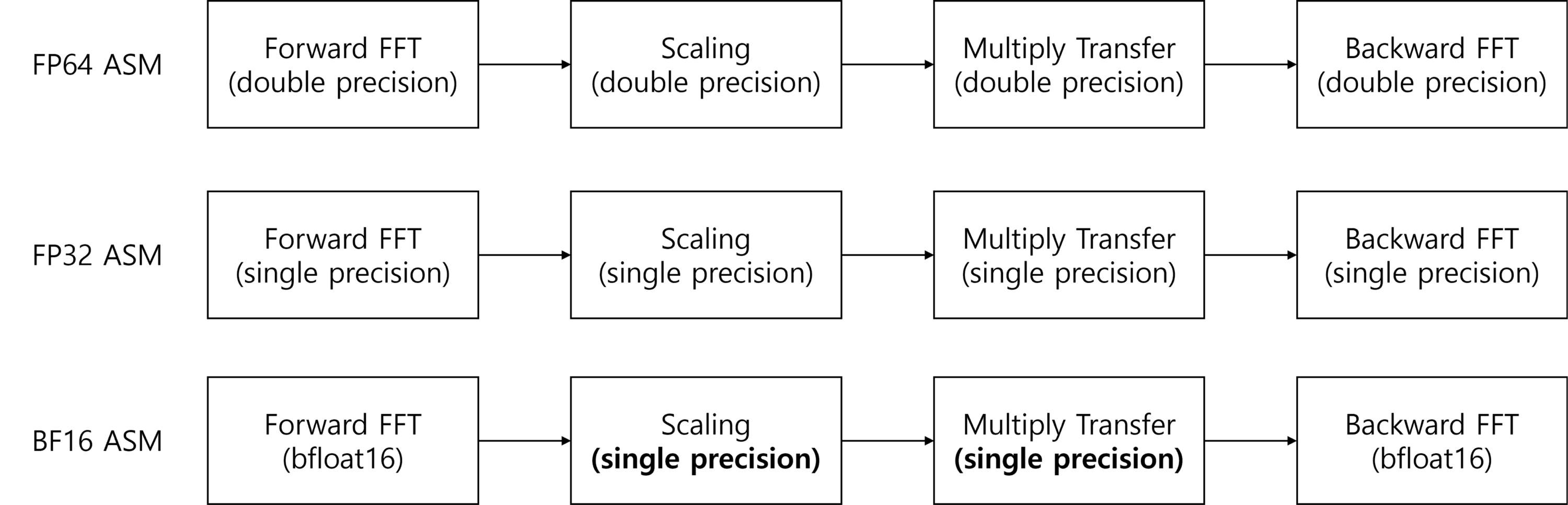
각 스펙트럼 방법의 처리 순서와 연산에 적용한 정밀도(FP64, FP32 and BF16)Fig. 2. Procedures of ASM(angular spectrum method) and used precisions(FP64, FP32 and BF16)

각 스펙트럼 방법을 이용하여 평면파 u(x,y,0)를 u(x,y,z)로 전파하기 위해서 푸리에 변환 F(수식 6)와 역푸리에 변환 F^-1(수식 7)를 이용한다. x, y, z는 3차원 공간좌표, f_x, f_y는 푸리에 도메인의 공간 좌표이다. k는 파수(wave number), λ는 빛의 파장이다. H(f_x, f_y,z)는 각 스펙트럼 방법의 전달 함수로 수식 5와 같다. × 는 아다마르 곱(Hadamard product)이다.

고속 푸리에 변환: 본 연구는 cuFFT^[18]를 사용하여 고속 푸리에 변환을 수행하였다. cuFFT는 배정밀도, 단정밀도, 반정밀도와 bfloat16을 지원하지만, 반정밀도와 bfloat16에 대해서는 크기가 2n인 행렬만 처리할 수 있다는 제약이 있다. 따라서, 본 연구의 실험에는 크기가 2n인 행렬이 사용되었다. cuFFT는 공간주파수 도메인의 영점을 조절할 수 있는, 중심 이산 푸리에 변환(centered discrete Fourier transform, CDFT)^[39,40] 또는 FFT-shift^[14,41] 기능을 제공하지 않는다. 따라서, 본 연구에서는 FFT-shift를 CUDA 환경에서 구현하여 FFT 수행 전, 후로 FFT-shift를 수행하였다.

스케일링(scaling): cuFFT는 역푸리에 변환 연산 시 Inverse FFT가 아닌 backward FFT를 수행한다. backward FFT의 수식 7과 같다.

backward FFT(수식 7)는 forward FFT(수식 6)의 값에 벡터 크기 N을 곱한 수를 나타낸다. 따라서, 본래 u(x) 값을 얻기 위해서는 backward FFT 값을 N으로 나누어야 한다.

오버플로우와 언더플로우: 스케일링 과정에서 행렬의 크기가 약 1,024*1,024일 때, 약 10⁶에 해당하는 값을 나누어야 한다. 이는 반정밀도의 최대 표현범위(65,504)를 초과한다. 전달함수연산은 빛의 파장(5.32e-9)를 제곱하고 곱하는 등의 높은 정밀도를 요구하기 때문에 반정밀도의 최소 표현 값(6.10e-5)의 범위를 벗어나는 문제가 발생한다. 이에 따라, 반정밀도는 본 논문의 실험대상에서 제외하였다. bfloat16 정밀도는 반정밀도에 비해 값을 표현할 수 있는 범위가 크지만 소수부의 크기가 매우 작기 때문에 스케일링과 전달함수 곱셈 수행 시 오차가 크게 증가하는 것을 확인하였다. 따라서, bfloat16의 두 연산은 단정밀도 연산으로 대체하였다 (그림 2).

Ⅴ. 홀로그램 품질 비교 및 분석

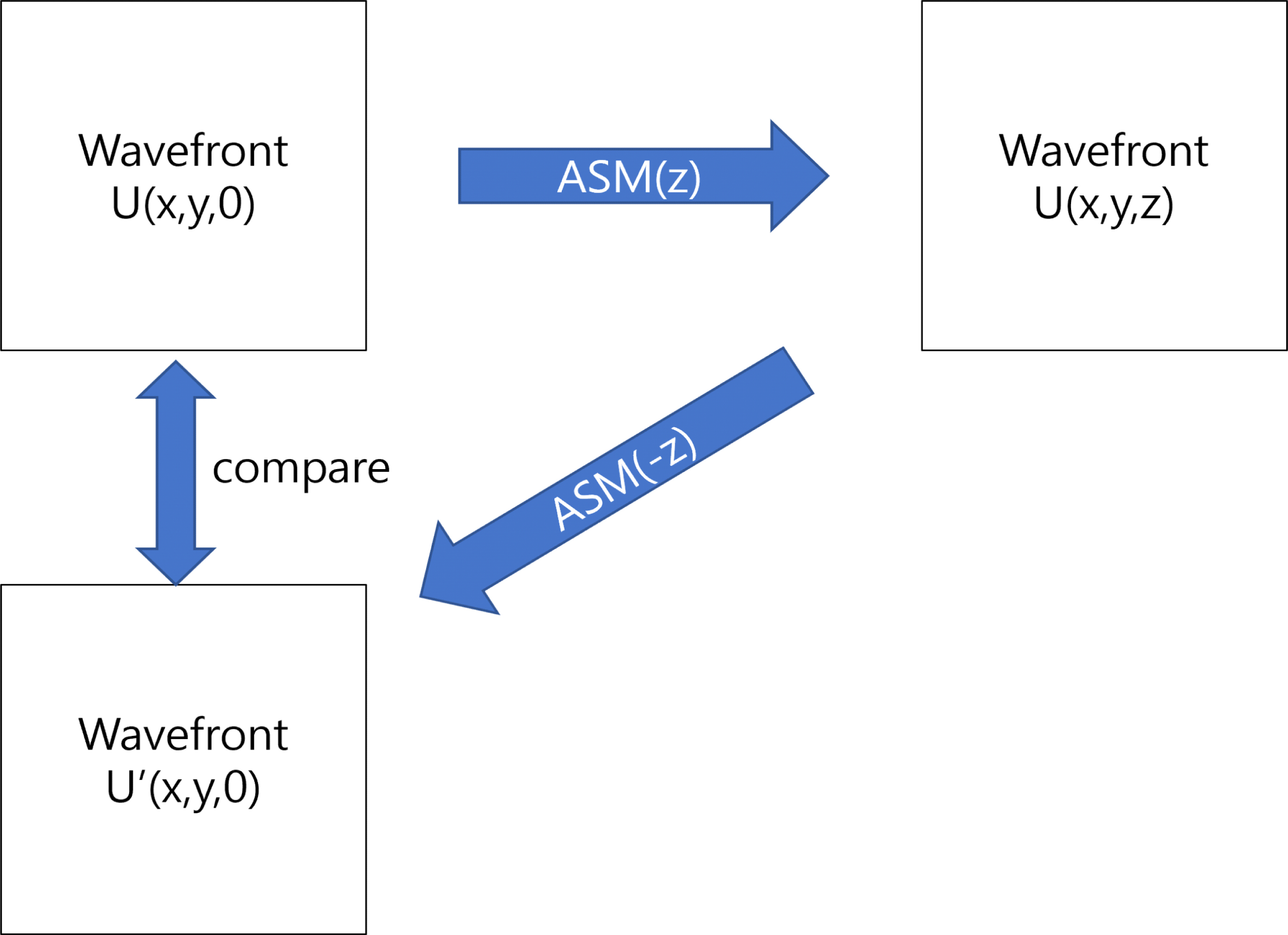
홀로그램 품질 비교를 위해서 본 연구에서는 그림 3과 같이 각 스펙트럼 방법의 정밀도별 오차를 비교하였다. 각 스펙트럼 방법을 이용하여 이미지 u(x,y,0)를 z축 이동하여 u(x,y,z) 로 전파한 후, u(x,y,z)를 -z축 이동하여 u'(x,y,0)으로 복구한다. 이때 원본 이미지 u(x,y,0)와 전파 이미지 u'(x,y,0)를 비교하여 각 스펙트럼 방법의 정밀도별 파동의 진폭(amplitude) 오차와 연산시간을 분석하였다.

그림 3.

홀로그램 품질 비교 방법Fig. 3. Comparing method for quality of a hologram

본 실험을 위해 사용한 연산장치는 RTX 3090 24GB이며 CUDA 11.7 환경에서 실험을 수행하였다. 실험에 사용한 각 스펙트럼 방법의 해상도는 8,192*8,192, 16,384*16,384로 DIV2K^[42]의 검증 세트를 선형 보간법을 통해 보간 하였다. 각 스펙트럼 연산에 이용한 파라미터는 λ=532nm, pixel pitch=8μm, z=0.09m이다. 정밀도는 배정밀도, 단정밀도, bfloat16을 이용하였다. 반정밀도의 경우, 표현 가능한 수의 범위가 파라미터에 미치지 못하여(4 장) 실험대상에서 제외하였다. 표 1는 각 정밀도 별 연산시간과 MSE(Mean Squared Error), PSNR(Peak Signal-to-Noise Ratio), SSIM(Structural Similarity Index Measure)을 보여준다. MSE, PSNR, SSIM은 각각 DIV2K 검증 세트를 기준으로 계산하였으며, MSE와 PSNR은 낮을수록, 그리고 SSIM은 높을수록 검증 세트와 유사한(정확한) 결과임을 말한다. 8,192*8,192 해상도의 경우, 배정밀도가 단정밀도에 비해 각각 2.78배, bfloat16에 비해 4.22배 연산시간이 더 많이 소요하였다. 이미지의 품질면에서는, 정밀도가 낮아질수록 MSE와 PSNR은 증가하고, SSIM은 낮아지는 결과를 보여준다. 즉, 정량적인 품질은 낮아짐을 의미한다. 하지만, 정밀도가 가장 낮은 bfloat16에서 MSE가 1.08e-05 수준으로, 일반 이미지의 양자화 수준인 8비트(256단계)에 매주 작은 수치이며, 정성적인 비교에서도 큰 차이를 확인하기 어려움을 확인했다(그림 5).

해상도가 16,384*16,384인 경우, 배정밀도의 연산시간이 단정밀도의 4.36배, bfloat16의 5.94배 소요되는 것을 확인할 수 있다. 이는 8,192*8,192에 비해 증가한 수치이며, 해상도가 커질수록 연산시간의 차이는 커짐을 보여준다. MSE, PSNR, SSIM 또한, 8,192*8,192 해상도의 경우에 비해 차이가 커졌으며, bfloat16의 MSE 수치가 높아졌고, PSNR과 SSIM 수치가 낮아졌다. 하지만, 여전히 정성적인 이미지 품질에 영향을 주기에는 작은 수치로, 홀로그램의 유의미한 품질 변화를 확인하기 어렵다 (그림 5).

단정밀도와 bfloat16의 연산속도를 비교하였을 때, 단정밀도의 연산시간이 8,192*8,192에서 1.52배, 16,384*16,384에서 1.36배 더 많이 소요되는 것으로 나타났다. 해상도가 커질수록 연산속도의 차이가 줄어드는 것으로 파악되었다. 이는 해상도가 커질수록 FFT 연산시간의 차이가 줄어들기 때문이다. 그림 4와 표 2은 정밀도가 각 스펙트럼 연산 과정에 미치는 영향을 분석하기 위해 각 스펙트럼 방법 연산 과정의 수행시간을 비교하였다. 본 연구에서 각 스펙트럼 방법의 연산과정은 그림 2와 같지만, Forward FFT와 Backward FFT 두 연산은 동일한 연산절차 (FFT-shift, cuFFT, FFT-shift)를 수행한다. 따라서, 그림 4와 표 3에서 FFT-shift, FFT, Scaling, Transfer(전달 함수)의 연산시간을 비교하였다. bfloat16과 단정밀도의 FFT 연산시간의 차이가 8,192*8,192는 1.89배, 16,384*16,384는 1.55배로 줄어드는 것을 확인할 수 있다. 또한, 전달함수 곱셈의 경우, bfloat16이 단정밀도 보다 많은 연산시간 소요하는 것을 확인할 수 있다. 본 연구의 실험에서, bfloat16은 정밀도가 낮아 전달함수를 표현하기 어렵기 때문에, 전달함수(수식 5)는 단정밀도로 연산하도록 하였다(4 장). 따라서, bfloat16와 단정밀도 사이의 데이터 변환 과정이 필요하며, 이 부하(overhead)로 전달함수 계산에 있어 bfloat16이 단정밀도에 비해 느린 현상이 발생한다. 하지만, 전달함수 외 다른 연산 부분에서는 데이터의 크기와 연산시간이 비례하는 것을 확인할 수 있다.

표 2.

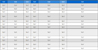
정밀도별 각 스펙트럼 방법 연산시간, MSE, PSNR, SSIMTable 2. Processing time, MSE, PSNR, SSIM of angular spectrum method in three precisions

그림 4.

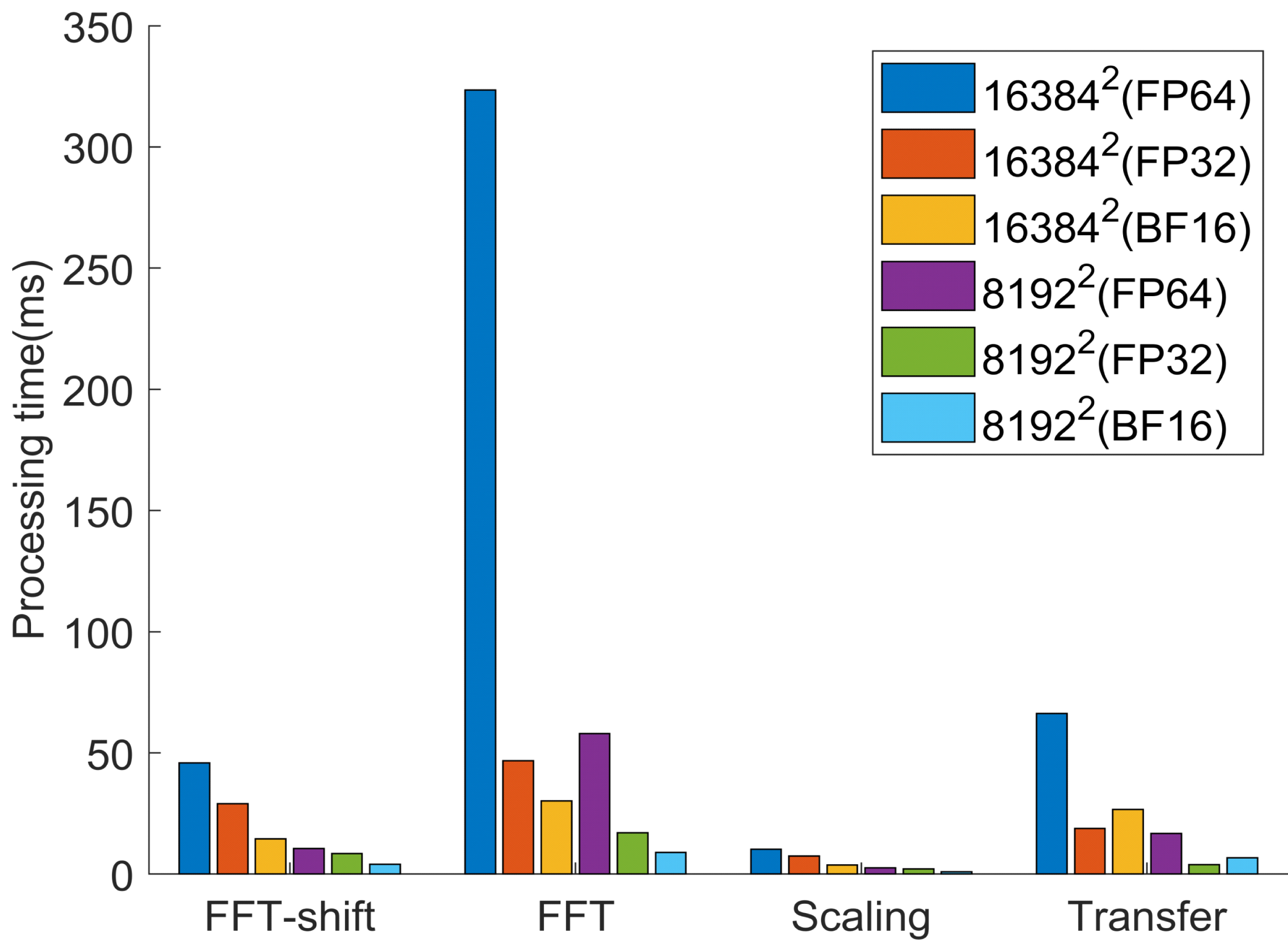
정밀도(FP64, FP32, BF16)에 따른 각 스펙트럼 방법의 수행절차별 연산시간 비교Fig. 4. Processing time of sub-steps of angular spectrum method with FP64, FP32 and BF16(bfloat16)

표 3

정밀도에 따른 각 스펙트럼 방법의 수행절차별 연산시간 비교(ms)Table 3. Processing time of sub-steps of angular spectrum method with FP64, FP32 and BF16(bfloat16)

그림 5

회절연산 이미지 비교Fig. 5. Comparison of diffraction images

Ⅵ. 결 론

본 논문은 CGH에서 핵심 연산인 회절 연산, 그중 각 스펙트럼 방법에 대한 연산 정밀도의 영향을 분석하였다. 배정밀도, 단정밀도, 그리고 bfloat16을 이용한 회절 연산을 수행하고, 생성된 홀로그램의 품질을 분석하였다. 그 결과, 반정밀도는 수 표현 범위의 한계로 홀로그램 생성에 사용하기 어렵지만, 같은 데이터 크기를 가지는 bfloat16은 데이터의 표현범위가 반정밀도에 비해 넓으며 홀로그램 연산에 대한 적용이 가능하다는 것을 확인하였다. 하지만, 일부 연산(예, 전달함수와 스케일링)에서는 bfloat16를 사용할 수 없음을 발견하였다. 따라서, 전달함수와 스케일링에 대해서는 단정밀도와 혼합하여 각 스펙트럼 방법을 구현하였다. 그 결과, bfloat16에 기반을 둔 회절 연산으로 준수한 품질의 홀로그램을 생성할 수 있었다. 또한, bfloat16를 사용함으로써, 배정밀도 및 단정밀도 사용 대비 각각 최대 5.94배, 1.52배 높은 연산 성능을 달성할 수 있음을 확인하였다. 또한, 생성된 홀로그램 품질에 유의미한 변화는 없는 것을 확인하였다.

본 논문에서는 낮은 정밀도를 이용한 홀로그램 연산의 가능성과 높은 연산성능을 확인하였다. 하지만, bfloat16의 정밀도 오차가 홀로그램의 해상도가 증가하면서 증가하는 것을 확인했다. 향후 연구에서는 해상도 증가에 따른 오차 증가를 상쇄할 수 있는 방법에 대해 연구하고자 한다. 특히, 홀로그램 연산에 사용하는 파라미터(예: 픽셀간격, 빛의 파장)등은 값이 너무 작기 때문에 연산 오차를 증가시킨다는 점에 착안하여, 파라미터의 값을 스케일링하여 연산할 수 있는 방법을 연구하고자 한다. 또한, 최근 텐서코어를 이용하여 합성곱 외 연산문제를 해결하는 방법이 연구되고 있으며, 홀로그램 생성에도 텐서코어를 이용하는 방법도 연구하고자 한다.

References

• Corda, R., Giusto, D., Liotta, A., Song, W., Perra, C., Recent Advances in the Processing and Rendering Algorithms for Computer-Generated Holography, Electronics, (2019), 8(5). [https://doi.org/10.3390/electronics8050556]
• Shimobaba, T., Ito, T., Computer Holography: Acceleration Algorithms and Hardware Implementations, CRC press, (2019).
• Matsushima, K., Introduction to Computer Holography: Creating Computer-Generated Holograms as the Ultimate 3D Image, Springer Nature, (2020).
• Wang, Y., et al. , Hardware implementations of computer-generated holography: a review, Optical Engineering, (2020), 59(10). [https://doi.org/10.1117/1.Oe.59.10.102413]
• Yuan, Y., Xun, G., Jia, K., Zhang, A., A Multi-view Deep Learning Method for Epileptic Seizure Detection using Short-time Fourier Transform, the Proceedings of the 8th ACM International Conference on Bioinformatics, Computational Biology,and Health Informatics, (2017). [https://doi.org/10.1145/3107411.3107419]
• Bracewell, R. N., The Fourier transform and its applications, McGraw-hill, New York, (1986).
• Yasuhito, O., Toshio, E., Naoya, M., Satoshi, M., An efficient, model-based CPU-GPU heterogeneous FFT library, the 2008 IEEE International Symposium on Parallel and Distributed Processing, (2008). [https://doi.org/10.1109/IPDPS.2008.4536163]
• Gu, L., Siegel, J., Li, X., Using GPUs to compute large out-of-card FFTs, the Proceedings of the international conference on Supercomputing, Tucson, Arizona, USA, (2011), Online. [https://doi.org/10.1145/1995896.1995937]
• Chen, S., Li, X., A hybrid GPU/CPU FFT library for large FFT problems, 2013 IEEE 32nd International Performance Computing and Communications Conference (IPCCC), 6-8 Dec. 2013. [https://doi.org/10.1109/PCCC.2013.6742796]
• Gholami, A., Hill, J., Malhotra, D., Biros, G., AccFFT: A library for distributed-memory FFT on CPU and GPU architectures, (2015), arXiv preprint arXiv:1506.07933.
• Zhao, Z., Zhao, Y., The Optimization of FFT Algorithm Based with Parallel Computing on GPU, 2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), 12-14 Oct. 2018. [https://doi.org/10.1109/IAEAC.2018.8577843]
• Takahashi, D., Fast Fourier transform algorithms for parallel computers, Springer, (2019).
• Kang, H., Lee, J., Kim, D., HI-FFT: Heterogeneous Parallel In-Place Algorithm for Large-Scale 2D-FFT, IEEE Access, (2021), 9, p120261-120273. [https://doi.org/10.1109/ACCESS.2021.3108404]
• Lee, J., Kang, H., Yeom, H.-j., Cheon, S., Park, J., Kim, D., Out-of-core GPU 2D-shift-FFT algorithm for ultra-high-resolution hologram generation, Opt. Express, (2021), 29(12), p19094-19112, 2021/06/07. [https://doi.org/10.1364/OE.422266]
• Sharp, D., Stoyanov, M., Tomov, S., Dongarra, J., A More Portable HeFFTe: Implementing a Fallback Algorithm for Scalable Fourier Transforms, 2021 IEEE High Performance Extreme Computing Conference (HPEC), 20-24 Sept. 2021, (2021), p1-5. [https://doi.org/10.1109/HPEC49654.2021.9622811]
• Ayala, A., Tomov, S., Stoyanov, M., Haidar, A., Dongarra, J., Performance Analysis of Parallel FFT on Large Multi-GPU Systems, 2022 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), (2022). [https://doi.org/10.1109/IPDPSW55747.2022.00072]
• Intel® oneAPI Math Kernel Library, https://www.intel.com/content/www/us/en/developer/tools/oneapi/onemkl.html#gs.i3mm29, accessed Nov. 24, 2022.
• cuFFT :: CUDA Toolkit Documentation, https://docs.nvidia.com/cuda/cufft/index.html, accessed Nov. 24, 2022.
• rocFFT API, https://docs.amd.com/bundle/rocFFT-release-rocm-rel-5.2/page/library.html, accessed Nov. 24, 2022.
• Frigo, M., Johnson, S. G., The Design and Implementation of FFTW3, Proceedings of the IEEE, (2005), 93(2), p216-231. [https://doi.org/10.1109/JPROC.2004.840301]
• Frigo, M., Johnson, S. G., FFTW: an adaptive software architecture for the FFT, Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP '98, 15-15 May 1998, (1998), 3, p1381-1384, Cat. No.98CH36181. [https://doi.org/10.1109/ICASSP.1998.681704]
• Wang, S., Kanwar, P., BFloat16: The secret to high performance on Cloud TPUs, (2019), 4, Google Cloud Blog.
• Burgess, N., Milanovic, J., Stephens, N., Monachopoulos, K., Mansell, D., Bfloat16 Processing for Neural Networks, 2019 IEEE 26th Symposium on Computer Arithmetic (ARITH), (2019). [https://doi.org/10.1109/ARITH.2019.00022]
• Kikuchi, Y., Fujita, K., Ichimura, T., Hori, M., Maddegedara, L., Calculation of Cross-correlation Function Accelerated by Tensor Cores with TensorFloat-32 Precision on Ampere GPU, Computational Science – ICCS 2022, Lecture Notes in Computer Science, (2022), p277-290, ch. Chapter 37.
• IEEE Standard for Floating-Point Arithmetic, IEEE Std 754-2019 (Revision of IEEE 754-2008), (2019), p1-84. [https://doi.org/10.1109/IEEESTD.2019.8766229]
• Shimobaba, T., Masuda, N., Ito, T., Simple and fast calculation algorithm for computer-generated hologram with wavefront recording plane, Opt. Lett., (2009), 34(20), p3133-3135, 2009/10/15. [https://doi.org/10.1364/OL.34.003133]
• Seznec, M., Gac, N., Ferrari, A., Orieux, F., A Study on Convolution using Half-Precision Floating-Point Numbers on GPU for Radio Astronomy Deconvolution, 2018 IEEE International Workshop on Signal Processing Systems (SiPS), 21-24 Oct. 2018, (2018), p170-175. [https://doi.org/10.1109/SiPS.2018.8598342]
• Maass, C., Baer, M., Kachelriess, M., CT image reconstruction with half precision floating-point values, Med Phys, (2011, Jul), 38(Suppl 1), pS95. [https://doi.org/10.1118/1.3528218]
• Ho, N. M., Wong, W. F., Exploiting half precision arithmetic in Nvidia GPUs, 2017 IEEE High Performance Extreme Computing Conference (HPEC), 12-14 Sept. 2017, (2017), p1-7. [https://doi.org/10.1109/HPEC.2017.8091072]
• Luszczek, P., Kurzak, J., Yamazaki, I., Dongarra, J., Towards numerical benchmark for half-precision floating point arithmetic, 2017 IEEE High Performance Extreme Computing Conference (HPEC), 12-14 Sept. 2017, (2017), p1-5. [https://doi.org/10.1109/HPEC.2017.8091031]
• Abdelfattah, A., Tomov, S., Dongarra, J., Towards Half-Precision Computation for Complex Matrices: A Case Study for Mixed Precision Solvers on GPUs, 2019 IEEE/ACM 10th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA), (2019). [https://doi.org/10.1109/ScalA49573.2019.00008]
• Abdelfattah, A., Tomov, S., Dongarra, J., Fast Batched Matrix Multiplication for Small Sizes Using Half-Precision Arithmetic on GPUs, 2019 IEEE International Parallel and Distributed Processing Symposium (IPDPS), (2019). [https://doi.org/10.1109/IPDPS.2019.00022]
• Blinder, D., Schelkens, P., Fast Low-Precision Computer-Generated Holography on GPU, Applied Sciences, (2021), 11(13). [https://doi.org/10.3390/app11136235]
• Markidis, S., Chien, S. W. D., Laure, E., Peng, I. B., Vetter, J. S., NVIDIA Tensor Core Programmability, Performance & Precision, 2018 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), (2018). [https://doi.org/10.1109/IPDPSW.2018.00091]
• Pisha, L., Ligowski, L., Accelerating non-power-of-2 size Fourier transforms with GPU Tensor Cores, 2021 IEEE International Parallel and Distributed Processing Symposium (IPDPS), (2021). [https://doi.org/10.1109/IPDPS49936.2021.00059]
• Sorna, A., Cheng, X., Azevedo, E. D., Won, K., Tomov, S., Optimizing the Fast Fourier Transform Using Mixed Precision on Tensor Core Hardware, 2018 IEEE 25th International Conference on High Performance Computing Workshops (HiPCW), 17-20 Dec. 2018, (2018), p3-7. [https://doi.org/10.1109/HiPCW.2018.8634417]
• Li, B., Cheng, S., Lin, J., tcFFT: A Fast Half-Precision FFT Library for NVIDIA Tensor Cores, 2021 IEEE International Conference on Cluster Computing (CLUSTER), (2021). [https://doi.org/10.1109/Cluster48925.2021.00035]
• Durrani, S., et al. , Accelerating Fourier and Number Theoretic Transforms using Tensor Cores and Warp Shuffles, 2021 30th International Conference on Parallel Architectures and Compilation Techniques (PACT), (2021). [https://doi.org/10.1109/PACT52795.2021.00032]
• Mugler, D. H., The Centered Discrete Fourier Transform and a parallel implementation of the FFT, 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 22-27 May 2011, (2011), p1725-1728. [https://doi.org/10.1109/ICASSP.2011.5946834]
• Vargas-Rubio, J. G., Santhanam, B., On the multiangle centered discrete fractional Fourier transform, IEEE Signal Processing Letters, (2005), 12(4), p273-276. [https://doi.org/10.1109/LSP.2005.843762]
• Abdellah, M., cufftShift: high performance CUDA-accelerated FFT-shift library, Proceedings of the High Performance Computing Symposium, Tampa, Florida, (2014).
• Agustsson, E., Timofte, R., Ntire 2017 challenge on single image super-resolution: Dataset and study, Proceedings of the IEEE conference on computer vision and pattern recognition workshops, (2017), p126-135. [https://doi.org/10.1109/CVPRW.2017.150]